دنباله
پاسخ : دنباله
اگه اشتباه نکنم ، باید همچین رابطه ای صدق کنه :

که 53 توش صدق میکنه.
چون اگه دقت کنین ، از جمله ی
 تا جمله ی
تا جمله ی
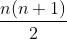 ، همشون برابر
، همشون برابر
 هستن.
هستن.
نه!
سوال اینو میخواد!
جمله اول یه دونه یکه.
جمله دوم و سوم دو هستش.
جمله چهارم و پنجم و ششم 3 هست(یه دونه یک-2تا دو-3تا3 و همینجوری ادامه پیدا میکنه)
بعد گفته اگه همینجوری دنباله رو بنویسیم جمله ی 1392ام چه عددی هست؟؟
گزینه ها 51 52 53 54
سوال اینو میخواد!
جمله اول یه دونه یکه.
جمله دوم و سوم دو هستش.
جمله چهارم و پنجم و ششم 3 هست(یه دونه یک-2تا دو-3تا3 و همینجوری ادامه پیدا میکنه)
بعد گفته اگه همینجوری دنباله رو بنویسیم جمله ی 1392ام چه عددی هست؟؟
گزینه ها 51 52 53 54
که 53 توش صدق میکنه.
چون اگه دقت کنین ، از جمله ی
پاسخ : دنباله
[SUB]1[/SUB]
میدانیم اگر m+n=c+d آنگاه:
a[SUB]m[/SUB]+a[SUB]n[/SUB]=a[SUB]c[/SUB]+a[SUB]d[/SUB]
البته این رابطه در دتباله عددی هست
در نتیجه:
a[SUB]1[/SUB]+a[SUB]14[/SUB]=100
a[SUB]2[/SUB]+a[SUB]13[/SUB]=100
a[SUB]3[/SUB]+a[SUB]12[/SUB]=100
a[SUB]4[/SUB]+a[SUB]11[/SUB]=100
a[SUB]5[/SUB]+a[SUB]10[/SUB]=100
a[SUB]6[/SUB]+a[SUB]9[/SUB]=100
a[SUB]7[/SUB]+a[SUB]8[/SUB]=100
حالا اگه همشونو با هم جمع بزنیم میشه
700=a[SUB]1[/SUB]+a[SUB]2[/SUB]+a[SUB]3+[/SUB]a[SUB]4+[/SUB]a[SUB]5+[/SUB]a[SUB]6+[/SUB]a[SUB]7+[/SUB]a[SUB]8+[/SUB]a[SUB]9+[/SUB]a[SUB]10+[/SUB]a[SUB]11+[/SUB]a[SUB]12+[/SUB]a[SUB]13+[/SUB]a[SUB]14[/SUB]
---- دو نوشته به هم متصل شده است ----
در دنباله ی a[SUB]n [/SUB]رابطه ی:
3a[SUB]n[/SUB]+a[SUB]n[/SUB]^3=3a[SUB]n[/SUB]^2+126+n
برقرار است
جمله 91 چند است؟
در یک تصاعد عددی a10+a5=100
مجموع 14 جمله اول
مجموع 14 جمله اول
میدانیم اگر m+n=c+d آنگاه:
a[SUB]m[/SUB]+a[SUB]n[/SUB]=a[SUB]c[/SUB]+a[SUB]d[/SUB]
البته این رابطه در دتباله عددی هست
در نتیجه:
a[SUB]1[/SUB]+a[SUB]14[/SUB]=100
a[SUB]2[/SUB]+a[SUB]13[/SUB]=100
a[SUB]3[/SUB]+a[SUB]12[/SUB]=100
a[SUB]4[/SUB]+a[SUB]11[/SUB]=100
a[SUB]5[/SUB]+a[SUB]10[/SUB]=100
a[SUB]6[/SUB]+a[SUB]9[/SUB]=100
a[SUB]7[/SUB]+a[SUB]8[/SUB]=100
حالا اگه همشونو با هم جمع بزنیم میشه
700=a[SUB]1[/SUB]+a[SUB]2[/SUB]+a[SUB]3+[/SUB]a[SUB]4+[/SUB]a[SUB]5+[/SUB]a[SUB]6+[/SUB]a[SUB]7+[/SUB]a[SUB]8+[/SUB]a[SUB]9+[/SUB]a[SUB]10+[/SUB]a[SUB]11+[/SUB]a[SUB]12+[/SUB]a[SUB]13+[/SUB]a[SUB]14[/SUB]
---- دو نوشته به هم متصل شده است ----
در دنباله ی a[SUB]n [/SUB]رابطه ی:
3a[SUB]n[/SUB]+a[SUB]n[/SUB]^3=3a[SUB]n[/SUB]^2+126+n
برقرار است
جمله 91 چند است؟
پاسخ : دنباله
سوالتون یکم غلطه ! باید ذکر کنه که عدد صحیحه جواب. وگرنه حل نمیشه.
به هر حال :

دقت کنید که اگه جای
 بذارید 7 ، پرانتزه میشه 31.
بذارید 7 ، پرانتزه میشه 31.
برا همینه که میگم با شرط صحیح بودن باید باشه.
در دنباله ی a[SUB]n [/SUB]رابطه ی:
3a[SUB]n[/SUB]+a[SUB]n[/SUB]^3=3a[SUB]n[/SUB]^2+126+n
برقرار است
جمله 91 چند است؟
3a[SUB]n[/SUB]+a[SUB]n[/SUB]^3=3a[SUB]n[/SUB]^2+126+n
برقرار است
جمله 91 چند است؟
به هر حال :
دقت کنید که اگه جای
برا همینه که میگم با شرط صحیح بودن باید باشه.
پاسخ : دنباله
ممنون ولی راحت تر هم میشه!
2a+13d=100

بنا بر این
7* 100 =700
[SUB]1[/SUB]
میدانیم اگر m+n=c+d آنگاه:
a[SUB]m[/SUB]+a[SUB]n[/SUB]=a[SUB]c[/SUB]+a[SUB]d[/SUB]
البته این رابطه در دتباله عددی هست
در نتیجه:
a[SUB]1[/SUB]+a[SUB]14[/SUB]=100
a[SUB]2[/SUB]+a[SUB]13[/SUB]=100
a[SUB]3[/SUB]+a[SUB]12[/SUB]=100
a[SUB]4[/SUB]+a[SUB]11[/SUB]=100
a[SUB]5[/SUB]+a[SUB]10[/SUB]=100
a[SUB]6[/SUB]+a[SUB]9[/SUB]=100
a[SUB]7[/SUB]+a[SUB]8[/SUB]=100
حالا اگه همشونو با هم جمع بزنیم میشه
700=a[SUB]1[/SUB]+a[SUB]2[/SUB]+a[SUB]3+[/SUB]a[SUB]4+[/SUB]a[SUB]5+[/SUB]a[SUB]6+[/SUB]a[SUB]7+[/SUB]a[SUB]8+[/SUB]a[SUB]9+[/SUB]a[SUB]10+[/SUB]a[SUB]11+[/SUB]a[SUB]12+[/SUB]a[SUB]13+[/SUB]a[SUB]14[/SUB]
---- دو نوشته به هم متصل شده است ----
در دنباله ی a[SUB]n [/SUB]رابطه ی:
3a[SUB]n[/SUB]+a[SUB]n[/SUB]^3=3a[SUB]n[/SUB]^2+126+n
برقرار است
جمله 91 چند است؟
میدانیم اگر m+n=c+d آنگاه:
a[SUB]m[/SUB]+a[SUB]n[/SUB]=a[SUB]c[/SUB]+a[SUB]d[/SUB]
البته این رابطه در دتباله عددی هست
در نتیجه:
a[SUB]1[/SUB]+a[SUB]14[/SUB]=100
a[SUB]2[/SUB]+a[SUB]13[/SUB]=100
a[SUB]3[/SUB]+a[SUB]12[/SUB]=100
a[SUB]4[/SUB]+a[SUB]11[/SUB]=100
a[SUB]5[/SUB]+a[SUB]10[/SUB]=100
a[SUB]6[/SUB]+a[SUB]9[/SUB]=100
a[SUB]7[/SUB]+a[SUB]8[/SUB]=100
حالا اگه همشونو با هم جمع بزنیم میشه
700=a[SUB]1[/SUB]+a[SUB]2[/SUB]+a[SUB]3+[/SUB]a[SUB]4+[/SUB]a[SUB]5+[/SUB]a[SUB]6+[/SUB]a[SUB]7+[/SUB]a[SUB]8+[/SUB]a[SUB]9+[/SUB]a[SUB]10+[/SUB]a[SUB]11+[/SUB]a[SUB]12+[/SUB]a[SUB]13+[/SUB]a[SUB]14[/SUB]
---- دو نوشته به هم متصل شده است ----
در دنباله ی a[SUB]n [/SUB]رابطه ی:
3a[SUB]n[/SUB]+a[SUB]n[/SUB]^3=3a[SUB]n[/SUB]^2+126+n
برقرار است
جمله 91 چند است؟
2a+13d=100
بنا بر این
7* 100 =700
پاسخ : دنباله
میشد خیلی راحت از جمله عمومی مشتق گرفت و مساوی صفر قرار داد ، اون وقت n=3 جواب بدست می اومد مستقیم !
( یعنی اگر به جای دنباله ، تابع با دامنه R رو هم در نظر میگرفتیم ، مینیمم اون تابع تو 3 بود. ) اون 2.5 رو چطور به دست آوردی؟ :219:
راه حل :

اگه 2.5 بذاریم که میشه : -923.75 که بیشتر از مقدار بالاست.
میشد خیلی راحت از جمله عمومی مشتق گرفت و مساوی صفر قرار داد ، اون وقت n=3 جواب بدست می اومد مستقیم !
( یعنی اگر به جای دنباله ، تابع با دامنه R رو هم در نظر میگرفتیم ، مینیمم اون تابع تو 3 بود. ) اون 2.5 رو چطور به دست آوردی؟ :219:
راه حل :
اگه 2.5 بذاریم که میشه : -923.75 که بیشتر از مقدار بالاست.
