پاسخ : ماراتن جبر (سطح پیشرفته)
ميگم چرا ثابت نميشه! :4: ولي براي راه حل شما زياد فرقي نمي كنه چون اون نامساوي كه توي پست قبل بهش اشاره كردم غلطه! پس زيادي سمت چپ رو كوچك كردين!
اصلا یه چیزی!! :4:
صورت سوال اشتباهه که! الان
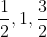 گذاشتم اشتباه شد. باید علامت نامساوی تو صورت سوال برعکس باشه که اشتباه نوشته شده !!
گذاشتم اشتباه شد. باید علامت نامساوی تو صورت سوال برعکس باشه که اشتباه نوشته شده !!
که اگه تصحیح شه راه منم کسی جرئت نمیکنه بهش گیر بده ! :4:
صورت سوال اشتباهه که! الان
که اگه تصحیح شه راه منم کسی جرئت نمیکنه بهش گیر بده ! :4:

