- ارسال ها
- 935
- لایک ها
- 1,654
- امتیاز
- 93
پاسخ : ماراتن جبر (سطح پیشرفته)
سوال جایی نیست !!! سوالی هست که طرح یک دانش آموز هستش !! حلشو بلد نیستم خودم .تو مث لینکس هم گذاشتم تقریبا 400-500 view داشته اما کسی جوابشو نذاشته . هرچند چندبار اونجا گفتم که بیاید جواب بدید و من نیاز به جواب این سوال دارم و ... اما کسی بلد نبوده !!
ببین ا.ذ. هم گفت تابع
 هم صدق میکنه خب ایده ی قبلیمو میتونیم تعمیم بدیم و بگیم تابع
هم صدق میکنه خب ایده ی قبلیمو میتونیم تعمیم بدیم و بگیم تابع
 هم صدق میکنه اما میدونیم فقط به ازای
هم صدق میکنه اما میدونیم فقط به ازای
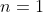 صحیحه خب پس حل من ناقصه و خودمم میدونم فقط میخوام اشکالشو پیدا کنم !!! ببخشید این سوال اخر حل نشد بگید مال کجاست البته راحت ازش نگذریم سوال خوبیه اقای ا.ذ. خودتون اگه راه حل دارید بذار !!!
صحیحه خب پس حل من ناقصه و خودمم میدونم فقط میخوام اشکالشو پیدا کنم !!! ببخشید این سوال اخر حل نشد بگید مال کجاست البته راحت ازش نگذریم سوال خوبیه اقای ا.ذ. خودتون اگه راه حل دارید بذار !!!





