ماراتن نظریه ی اعداد (سطح ممتاز)
[center:ceecf2be45]کافیه احکام زیرو رو ثابت کنیم : [/center:ceecf2be45]
[center:ceecf2be45]
 [/center:ceecf2be45]
[/center:ceecf2be45]
[center:ceecf2be45]ابتدا توجه کنید که اگر
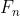 اول باشه و
اول باشه و
 ,
,
 هم اوله.[/center:ceecf2be45]
هم اوله.[/center:ceecf2be45]
[center:ceecf2be45]پس قسمت اول آسونه و کافیه دنباله رو به پیمانه 4 در نظر بگیرید تا بفهمید
&space;\Rightarrow&space;m\equiv&space;4(mod6)) . که طبق اون چیزی که ابتدا گفتیم اول نیست.[/center:ceecf2be45]
. که طبق اون چیزی که ابتدا گفتیم اول نیست.[/center:ceecf2be45]
[center:ceecf2be45]حالا برای قسمت دوم , اول توجه کنید
 [/center:ceecf2be45]
[/center:ceecf2be45]
[center:ceecf2be45]حالا ازین جا به بعدش آسونه (مثه قبلیس , و با استفاده ازون قضیه مربع کامل ها فیبو ! ) ولی با این حال اگه این عربی ملعون تموم شه بقیشم مینویسم. [/center:ceecf2be45]
[center:ceecf2be45]با اون اتحادیم که SHOKI گفت دیگه مسئله تموم شدس . اگه میخواین مسئله جدید بزارید . ممنون......تا بعد ![/center:ceecf2be45]
[center:ceecf2be45]
[center:ceecf2be45]ابتدا توجه کنید که اگر
[center:ceecf2be45]پس قسمت اول آسونه و کافیه دنباله رو به پیمانه 4 در نظر بگیرید تا بفهمید
[center:ceecf2be45]حالا برای قسمت دوم , اول توجه کنید
[center:ceecf2be45]حالا ازین جا به بعدش آسونه (مثه قبلیس , و با استفاده ازون قضیه مربع کامل ها فیبو ! ) ولی با این حال اگه این عربی ملعون تموم شه بقیشم مینویسم. [/center:ceecf2be45]
[center:ceecf2be45]با اون اتحادیم که SHOKI گفت دیگه مسئله تموم شدس . اگه میخواین مسئله جدید بزارید . ممنون......تا بعد ![/center:ceecf2be45]
mmath گفت
خیلی خیلی زیبا بود !!!!!!

 البته خدا کنه اشتباه نکرده نباشم .
البته خدا کنه اشتباه نکرده نباشم .
جوابش : هر m غیر از یک
چرا : مقسوم علیه های
 را در نظر میگیریم . بعد Zsigmondy , (البته بعدش که حل شد فهمیدم بدون Zsigmondy هم میشه)
را در نظر میگیریم . بعد Zsigmondy , (البته بعدش که حل شد فهمیدم بدون Zsigmondy هم میشه)
اگه بازم توضیح می خواد بفرمایید , اگه نه , لطفا یکی یه مسئله بزاره ...


جوابش : هر m غیر از یک
چرا : مقسوم علیه های
اگه بازم توضیح می خواد بفرمایید , اگه نه , لطفا یکی یه مسئله بزاره ...
[center:05b73bfa0e]
ثابت کنید عددی وجود ندارد که در دنباله ی
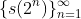 بی نهایت بار تکرار شود. (
بی نهایت بار تکرار شود. (
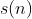 مجموع ارقام عدد طبیعی
مجموع ارقام عدد طبیعی
 است.)
است.)
[/center:05b73bfa0e][center:ef081becc7]فرض کنید [/center:ef081becc7]
[center:ef081becc7]
 [/center:ef081becc7]
[/center:ef081becc7]
[center:ef081becc7]حالا با توجه به گنگ بودن
 میشه گفت از یه جایی به بعد مجموع ارقام از یه حدی بیشتره[/center:ef081becc7]
میشه گفت از یه جایی به بعد مجموع ارقام از یه حدی بیشتره[/center:ef081becc7]
[center:ef081becc7]یا[/center:ef081becc7]
[center:ef081becc7]میشه دنباله ای به طول دلخواه با خاصیت [/center:ef081becc7]
[center:ef081becc7]

 [/center:ef081becc7]
[/center:ef081becc7]
[center:ef081becc7]ساخت که با فرض در تناقضه !!!ه[/center:ef081becc7]
[center:ef081becc7]
[center:ef081becc7]حالا با توجه به گنگ بودن
[center:ef081becc7]یا[/center:ef081becc7]
[center:ef081becc7]میشه دنباله ای به طول دلخواه با خاصیت [/center:ef081becc7]
[center:ef081becc7]
[center:ef081becc7]ساخت که با فرض در تناقضه !!!ه[/center:ef081becc7]
mmath گفت
[center:6abcfaaf8d]فرض کنید [/center:6abcfaaf8d]
[center:6abcfaaf8d]
 [/center:6abcfaaf8d]
[/center:6abcfaaf8d]
[center:6abcfaaf8d]حالا با توجه به گنگ بودن
 میشه گفت از یه جایی به بعد مجموع ارقام از یه حدی بیشتره[/center:6abcfaaf8d]
میشه گفت از یه جایی به بعد مجموع ارقام از یه حدی بیشتره[/center:6abcfaaf8d]
[center:6abcfaaf8d]یا[/center:6abcfaaf8d]
[center:6abcfaaf8d]میشه دنباله ای به طول دلخواه با خاصیت [/center:6abcfaaf8d]
[center:6abcfaaf8d]

 [/center:6abcfaaf8d]
[/center:6abcfaaf8d]
[center:6abcfaaf8d]ساخت که با فرض در تناقضه !!!ه[/center:6abcfaaf8d]
[center:6abcfaaf8d]
[center:6abcfaaf8d]حالا با توجه به گنگ بودن
[center:6abcfaaf8d]یا[/center:6abcfaaf8d]
[center:6abcfaaf8d]میشه دنباله ای به طول دلخواه با خاصیت [/center:6abcfaaf8d]
[center:6abcfaaf8d]
[center:6abcfaaf8d]ساخت که با فرض در تناقضه !!!ه[/center:6abcfaaf8d]
اما در مورد اثبات شما: شاید بشه فهمید که کلیت راه حل شما چیه. اما این نوع نوشتن، برای اکثر بچه ها قابل استفاده نیست. هدف مطرح شدن این سوال ها هم اینه که بچه ها از راه حل این سوال ها چیزی یاد بگیرند.
بنابراین لطف کنید راه حل هاتون رو کامل بنویسید.
سوال بعد:
[center:6abcfaaf8d]
ثابت کنید عددی وجود ندارد که در دنباله ی
mohammad_72 گفت
سوال 9 چی شد ؟؟؟
@mmath : میتونید راه حلتون برای سوال 12 رو بیشتر توضیح بدید.
@mmath : میتونید راه حلتون برای سوال 12 رو بیشتر توضیح بدید.
برای سوال 9 کسی جواب کاملی نداشت. البته shoki یه ایده ای رو داد که مسئله به حالتی که a,b مربع کاملند محدود شد. هر چند به نظر می رسه اثبات مسئله توی این حالت از حکم مسئله قوی تر باشه. سوال 12 هم صورت کلی سوال IMO03 هست،
فرض می کنیم
 عامل اولی از
عامل اولی از
 باشد و
باشد و
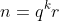 . در این صورت
. در این صورت
[center:773d6aa000]
 [/center:773d6aa000]
[/center:773d6aa000]
بنابراین
 عامل اولی مانند
عامل اولی مانند
 دارد که
دارد که
 . ادعا می کنیم که
. ادعا می کنیم که
 در مسئله صدق می کند. اگر به ازای عددی مانند
در مسئله صدق می کند. اگر به ازای عددی مانند
 داشته باشیم
داشته باشیم
 آن گاه
آن گاه
[center:773d6aa000]
 [/center:773d6aa000]
[/center:773d6aa000]
از طرفی
 . چراکه در غیر این صورت
. چراکه در غیر این صورت
 و لذا
و لذا
[center:773d6aa000]
 [/center:773d6aa000]
[/center:773d6aa000]
که غیر ممکن است.
حال از این که
 و
و
 نتیجه می گیریم
نتیجه می گیریم
 . که متناقض با فرض اولیه ی ماست.
. که متناقض با فرض اولیه ی ماست.
[center:773d6aa000]
[/center:773d6aa000]
فرض می کنیم
[center:773d6aa000]
بنابراین
[center:773d6aa000]
از طرفی
[center:773d6aa000]
که غیر ممکن است.
حال از این که
[center:773d6aa000]
[/center:773d6aa000]







