ماراتن نظریه ی اعداد (سطح ممتاز)

behrooz1373 · 1389/3/20

اگر p عامل اولی از n باشد و n=pt طبق فرض p|t-1 پس

$(p,t)=1$

و این یعنی اینکه n خالی از مربع است حال داریم

$1^{n-1}+2^{n-1}+...+(n-1)^{n-1}+1\equiv t(1^{pt-1}+...+(p-1)^{pt-1})+1\equiv t(1+...+1)+1\equiv (p-1)t+1\equiv -t+1\equiv 0 (mod p)$

درعبارت بالا از اینکه

$t\equiv 1 (mod p)$

و

$t\equiv 1 (mod p-1)$

و قضیه فرما استفاده شده است.حال چون n خالی از مربع است و برای هرعامل n حکم را ثابت کردیم پس برای n هم حکم ثابت است.

mohammad_72 · 1389/3/20

فرض می‌کنیم

$d = (n-1, p-1)$

و g ریشه‌ی اولیه ای به پیمانه‌ی p باشه.

$(1^{n-1}+...+n^{n-1})+1 \equiv t(1^{n-1}+...+(p-1)^{n-1})+1 \equiv t(g^d+g^{2d}+...+g^{(p-1)d})+1 \equiv t(\frac{g^{pd}-g^d}{g^d-1})+1$

اگه

$d \ne p-1$

این عبارت به پیمانه‌ی p با 1 همنهشت میشه. پس

$d = p-1$

یعنی

$p-1|\frac{n}{p}-1$

عبارت مساله هم همنهشت میشه با

$-t+1$

پس حله.

shoki · 1389/3/20

شرمنده اگه قوانین رو زیر پا می ذارم

... یه سوال قشنگ ...
سوال 16 :
بزرگترین مقدار n رو پیدا کنید که این خاصیت رو داشته باشه: اگر p,q,t,s اعداد صحیح باشند و s و t مثبت باشند و

و

آنگاه

.

mohammad_72 · 1389/3/20

مطمئنین بزرگترین n با این خاصیت وجود داره ؟
من فعلا این عددا رو پیدا کردم که تو شرط مساله صدق می‌کنن :
2, 6, 42, 42*43, 42*43*499

mahanmath · 1389/3/20

mohammad_72 گفت

http://www.artofproblemsolving.com/Forum/viewtopic.php?f=57&t=320271

M_Sharifi · 1389/3/20

توی محاسباتت اشتباه کردی. 498 عامل 83 داره نه 43.

shoki · 1389/3/20

Mr.mmath
صد هزار بار گفته شده لینک نکنید ... اگه قراره این طوری باشه و بقیه ی بچه ها مثل شما همین کار رو بکنن اون وقت فکر می کنید چی می شه ؟؟؟؟ اون وقت دیگه سوالی مطرح نمی شه ... اگه لینکشو و جوابشو می دونید فقط راهنمایی بذارید یا جوابشو بذارید (به صورت کامل)

mohammad_72 · 1389/3/20

M_Sharifi گفت

انگار نمی‌تونم تو یه سوال سوتی ندم !!!
چقدر به جواب نزدیک بودم !

$\300dpi \huge 17$

اعداد صحیح a و b و c مفروضند. ثابت کنید این دو حکم معادلند.
I ) بی‌نهایت عدد اول p وجود داره که

$\left ( \frac{a}{p} \right )=\left ( \frac{b}{p} \right )=\left ( \frac{c}{p} \right )=-1$

II ) اعداد a و b و c و abc مربع کامل نیستند.

mahanmath · 1389/3/20

bebakhshid ,

... albate manam havasam bood

az oon moghe ke soalo gozashti ke linkesho nazadam!!. didam ishoon kheily be javab nazdike

(ghablesham ye ghesmati az raho ke estefade az rishe avallie dashto gofte boodan.)

badesham man harfe shomaro kamelan ghabool daram va age post hamam negah konid mibinid in avalin barie ke link kardam.

Baraye soale 17 : khodet rahe halle sade dari ?
chon man ye soal shabih in didam ke zaheresh kheily asoon bod vali rahesh az kolle ketabe M.Mirzakhani estefade mikard.

bazam bebakhshid///mazerat

sorry for Farsi + English = FiNgLiSh

mohammad_72 · 1389/3/20

آره، راه حلی که من برای این سوال سراغ دارم از دیریکله ، باقیمانده‌ی چینی
و قانون تقابل درجه‌ی دو استفاده می‌کنه. میتونید سوالی که دیدید رو بذارید ؟

M_Sharifi · 1389/3/20

در واقع یه طرف حکم که به وضوح درسته.
برای طرف دوم، اولا ثابت میشه که برای هر

$a,b$

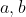که مربع کامل نباشند، بی نهایت عدد اول وجود داره که به پیمانه ی نامانده بشن. برای اثبات این مطلب فرض می کنیم

$p_1,p_2,\ldots,p_k$

و

$q_1,q_2,\ldots,q_t$

عوامل دارای توان فرد در

$a$

و

$b$

اند. برای این منظور کافیه که

$p\equiv 1\pmod 8$

و

$p$

به پیمانه ی فرد تا از عوامل اول فرد در

$p_1,p_2,\ldots,p_k$

و فردتا از عوامل اول فرد

$q_1,q_2,\ldots,q_t$

نامانده بشه. این کار هم به وضوح امکان پذیره. مگه در حالتی که یکی از این مجموعه ها

$\{2\}$

و اون یکی

$\{2,q_2,\ldots,q_k\}$

باشه، که در این صورت فرض می کنیم

$p\equiv 5\pmod8$

و هم چنین

$p$

رو به پیمانه ی هر کدوم از

$q_2,\ldots,q_k$

با یه مانده (مثلا 1) همنهشت می گیریم. با این انتخاب کافیه که

$p$

در دستگاه همنهشتی های ایجاد شده صدق کنه، که طبق قضیه ی دیریکله بی نهایت از این اعداد اول وجود داره.
در ادامه با توجه به این که

$abc$

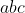مربع کامل نیست، نتیجه می گیریم که یا همه ی عوامل اولی که توان فردی در

$a,b,c$

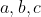دارند با هم یکسان اند، که اون موقع کافیه یکی از اعداد

$a,b,c$

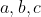به پیمانه ی

$p$

مانده بشه و یا عامل اولی مانند

$r$

وجود داره که فقط توی یکی از اعداد

$a,b,c$

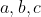با توان فرد ظاهر شده. در این صورت اگر مثلا

$r\mid c$

و

$r\ne2$

عدد اول

$p$

را طوری در نظر می گیریم که به پیمانه ی

$a,b$

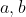نامانده بشه. حالا عوامل اولی که توی

$c$

اند ولی توی

$a,b$

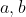نیستند رو در نظر می گیریم و

$p$

رو طوری انتخاب می کنیم که به پیمانه ی این عوامل طوری مانده و یا مانده بشه که در نهایت به پیمانه ی فرد تا از عوامل اول

$c$

نامانده بشه. با توجه به وجود

$r$

چنین انتخابی امکان پذیره. مگه این که

$r=2$

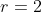که اون موقع هم میشه بحث مشابهی انجام داد. در نهایت هم باز قضیه ی دیریکله وجود بی نهایت از این اعداد اول رو تضمین می کنه.
البته اثبات این که مثلا بی نهایت تا

$p$

داریم که عدد غیر مربع کامل

$a$

نامانده بشه بدون دیریکله هم امکان پذیره. بنابراین احتمالا بدون دیریکله هم بشه این مسئله رو حل کرد.

mohammad_72 · 1389/3/20

حالا یه تعمیم از مساله‌ی 17 !

$\300dpi \huge 18$

اعداد a_1 , a_2, ..., a_n مفروضند. ثابت کنید دو حکم زیر هم ارزند:
I ) بیشمار عدد اول مانند p وجود دارد که

$\left (\frac{a_1}{p} \right )=\left (\frac{a_2}{p} \right )=...=\left (\frac{a_n}{p} \right )=-1$

II ) حاصلضرب هیچ فردتایی از اعداد a_1 تا a_n مربع کامل نیست.

M_Sharifi · 1389/3/21

راه حل سوال 18 تفاوت چندانی با سوال 17 نداره و میشه به صورت استقرایی استدلال سوال 17 رو تعمیم داد. چون اساس این دوتا راه حل یکسانه، سوال 19 رو مطرح می کنیم:

[center:020a79d540]

$\300dpi \huge 19$

برای مجموعه ی متناهی

$P$

از اعداد اول، ثابت کنید عدد طبیعی

$x$

وجود دارد که برای هر

$p\in P$

بتوان آن را به فرم

$a^p+b^p$

نمایش داد (

$a,b\in\Bbb N$

)، اما برای هیچ عدد اول

$p\not\in P$

این نوع نمایش امکان پذیر نباشد.

[/center:020a79d540]

mohammad_72 · 1389/3/21

M_Sharifi گفت

چه جوری ؟ میشه یکم توضیح بدین ؟

M_Sharifi · 1389/3/21

mohammad_72 گفت

در مورد وجود بی نهایت عدد اول

$p$

که

$a$

نامانده بشه، اثبات این جوریه که ثابت می کنیم برای هر مجموعه ی دلخواه

$\{p_1,p_2,\ldots,p_k\}$

از اعداد اول (که این اعداد اول، با عوامل اول

$a$

اشتراکی ندارند) عددی اول مانند

$p$

متمایز از

$p_1,p_2,\ldots,p_k$

وجود داره که

$a$

مانده ی درجه ی دوم به پیمانه ی

$p$

میشه. این موضوع نامتناهی بودن تعداد این اعداد اول رو هم ثابت می کنه.
برای اثبات، طبق قضیه ی باقی مانده چینی عددی طبیعی مانند

$x$

وجود داره که به پیمانه ی 8 برابر 1 و به پیمانه ی

$p_1,p_2,\ldots,p_k$

و عوامل اول

$a$

(به جز یکی) مانده بشه (مثلا 1) و به پیمانه ی اون یه عامل باقی مانده از

$a$

نامانده بشه. حالا میشه ثابت کرد که

$x$

عامل اولی داره که

$a$

نامانده اش میشه. (در واقع اگر

$\{q_1,\ldots,q_t\}$

عوامل اول با توان فرد در

$x$

باشند،

$\prod_{i=1}^t (\frac a{q_i})=-1$

که وجود چنین عامل اولی رو ثابت میکنه).
فقط حالتی می مونه که تنها عامل اول با توان فرد در

$a$

عامل 2 باشه. که در این صورت باید ثابت کنیم مثلا بی نهایت عدد اول 8k+3 داریم که بدون قضیه ی دیریکله هم اثباتش امکان پذیره.

mahanmath · 1389/3/21

بی
نهایت عدد اول 8k+3 داریم :

فرض کنید متناهی هستند . مثلا P_1 , ... , P_k حالا عوامل Q رو در نظر بگیرید که Q=(P_1...P_k)^2 +2 هست.

اینو گفتم (با این که میدونستم خیلی هاتون میدونستید

) تا یه راهنمایی برای مسئله جدید (19) باشه ...

mohammad_72 · 1389/3/22

اگه X حاصلضرب اعضای p باشه 2 به توان X+1 جواب مساله‌ی 19 هست !

M_Sharifi · 1389/3/22

mmath گفت

می تونی راه حلت رو کامل بنویسی؟

M_Sharifi · 1389/3/22

mohammad_72 گفت

درسته. سوال بعد:
[center:9e5fb48f67]

$\300dpi \huge 20$

فرض کنید

$\sigma(n)$

مجموع مقسوم علیه های مثبت عدد طبیعی

$n$

است. ثابت کنید برای هر

$k$

، می توان

$k$

عدد متوالی پیدا کرد که برای هر یک از این اعداد مانند

$n$

، داشته باشیم

$\sigma(n)>2n$

.

[/center:9e5fb48f67]

mohammad2004 · 1389/3/27

میدونیم

واگراست . اعداد اولو از 2 شروع می کنیم و تا یه جایی ادامه بدیم که

از 1 بیشتر بشه ادامه میدیم و دوباره این کارو انجام میدیم. حالا میدونیم اگه n به این چند تا عدد اول بخشپذیر باشه جمع مقسوم علیه هاش از 2n بیشتره. پس میخوایم x به این عددها ، x+1 به دسته بعدی ، ... بخشپذیر باشه که طبق باقیمانده چینی جواب داره

ماراتن نظریه ی اعداد (سطح ممتاز)

New Member

New Member

New Member

New Member

New Member

راهبر ریاضی

New Member

New Member

New Member

New Member

راهبر ریاضی

New Member

راهبر ریاضی

New Member

راهبر ریاضی

New Member

New Member

راهبر ریاضی

راهبر ریاضی

New Member