اثبات گنگ بودن
- شروع کننده موضوع happymoj
- تاریخ شروع
- برچسپ ها اثبات استفاده استقرا اعداد اعداد حقیقی اعداد صحیح تساوی تعریف حقیقی راهنمایی ریشه سوال قضیه چند جمله ای
- ارسال ها
- 107
- لایک ها
- 53
- امتیاز
- 0
پاسخ : سوال بنیادی
:179:
خوب حالا یه راهه دیگه بگم:
ما میتونیم روی توان رادیکال
استقرا بزنیم و بگیم در صورتی این عبارت گویاست که
توان رادیکال
رو عاد کنه ولی ما داریم که
رادیکال
رو عاد نمیکنه در نتیجه این عدد گنگه!! :225:
پس حرف شما معنیش اینه که اگه
گویا باشه, اون عبارت هم گویاست دیگه......حالا اگه
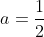باشه چه اتفاقی میفته؟؟
خوب حالا یه راهه دیگه بگم:
ما میتونیم روی توان رادیکال
پاسخ : سوال بنیادی
چطوری روی اعداد حقیقی استقرا میزنین؟ و این که عاد کردن رو برای اعداد حقیقی چی تعریف می کنین که میگین
نمیتونه بر
بخش پذیر باشه؟ ضمنا اگه میشه دلیل اون بخشی که قرمز کردم رو هم بگین. ممنون
:179:
خوب حالا یه راهه دیگه بگم:
ما میتونیم روی توان رادیکال
استقرا بزنیم و بگیم در صورتی این عبارت گویاست که
توان رادیکال
رو عاد کنه ولی ما داریم که
رادیکال
رو عاد نمیکنه در نتیجه این عدد گنگه!! :225:
خوب حالا یه راهه دیگه بگم:
ما میتونیم روی توان رادیکال
- ارسال ها
- 107
- لایک ها
- 53
- امتیاز
- 0
پاسخ : سوال بنیادی
در اون قسمت قرمز منظورم اینه که توانش باید زوج باشه تا عبارت گویا شه و فکر می کنم بشه رو این قسمت استقرا زد! اینطور نیست؟! در صورتی که رادیکال
جزو این اعداد نیست پس گنگه.البته شما مطمئنا بیشتر از من میدونید و اگر غلطه لطفا یه راهنمایی کوچولو بکنید تا بهتر بتونم فکر کنم. :173:
چطوری روی اعداد حقیقی استقرا میزنین؟ و این که عاد کردن رو برای اعداد حقیقی چی تعریف می کنین که میگین
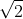نمیتونه بر
بخش پذیر باشه؟ ضمنا اگه میشه دلیل اون بخشی که قرمز کردم رو هم بگین. ممنون
پاسخ : سوال بنیادی
ببینید من خودم جواب این سوالو نمی دونم, ولی اینو میدونم که زوج یا فرد بودن, برای اعداد صحیح تعریف میشه, پس اگه شما بگین: اگر توان
توی مجموعه اعداد صحیح زوج باشه اونوقت عبارتمون گویا میشه, این حرف درسته, ولی نمی تونید این حرف رو برای اعداد حقیقی بزنید چون اونجا زوج و فرد بودن رو معنی نکردیم!!!!
ضمنا, اعداد حقیقی مثل اعداد صحیح گسسته نیستن که بشه استقرا رو توش بکار برد.
ببینید من خودم جواب این سوالو نمی دونم, ولی اینو میدونم که زوج یا فرد بودن, برای اعداد صحیح تعریف میشه, پس اگه شما بگین: اگر توان
ضمنا, اعداد حقیقی مثل اعداد صحیح گسسته نیستن که بشه استقرا رو توش بکار برد.
- ارسال ها
- 107
- لایک ها
- 53
- امتیاز
- 0
پاسخ : سوال بنیادی
در سال 1900 هیلبرت 23 مسئله ی عمیق و اساسی در ریاضیات اون دوران رو بیان میکنه.مسئله هفتم مربوط به جبری بودن یا نبودن
برای
و
های جبری است. (جبری بودن عدد
به این معنی است که چند جمله ای ناصفر
در
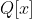یافت بشه که
=0)
) Gelfond و Schneider به طور مستقل ثابت کردن که
متعالی است یعنی جبری نیست. به این ترتیب
و اعداد مشابه این نه تنها گنگ هستند بلکه ریشه ی هیچ چند جمله ای ضرایب گویایی نیستند. این که آیا اعداد زیر جبری هستند یا نه تا به حال بدون پاسخ مانده است :
http://en.wikipedia.org/wiki/Hilbert's_seventh_problem
در سال 1900 هیلبرت 23 مسئله ی عمیق و اساسی در ریاضیات اون دوران رو بیان میکنه.مسئله هفتم مربوط به جبری بودن یا نبودن
http://en.wikipedia.org/wiki/Hilbert's_seventh_problem
آخرین ویرایش توسط مدیر