ریشه سوم دو
- ارسال ها
- 107
- لایک ها
- 53
- امتیاز
- 0
پاسخ : ریشه سوم دو
نه.یه مشکلی هست.ما نمی دونیم به ازای چه ایکسی مقدار تابع 2 شده.مشکل اصلی ما هم همینه.روش های تخمینی خوبی برای حل معادلات f(x)=0 وجود دارن که بهترین اونها در حد نه زیاد پیشرفته بسط تیلور و تکرار نیوتونه.
این هم یه مقاله فوق العاده خوب.پارسال کار و زندگیم شده بود رفتن دنبال انواع و اقسام این روش ها.الان از هر کدومشون یه چیزایی بلدم.یادگرفتن اینها برای سال اول و دومیا مستحبه.اما سال سومیا مخصوصا المپیادفیزیکیا و نجومیا باید حتما بلد باشن.تقریبا همه شون رو تا ترم 3 دانشگاه یادمیگیریم.زیاد هم سخت نیستند.فقط باید به مفاهیم تابع و مشتق مسلط باشید.
راه من اینه :
برای نشان دادن ریشه ی سوم دو روی محور ابتدا تابع y=x^3رارسم کنیدسپس ازمقدارy=2استفاده کنیدواز آن نقطه بر محور xهاعمود کنید
درسته ؟
برای نشان دادن ریشه ی سوم دو روی محور ابتدا تابع y=x^3رارسم کنیدسپس ازمقدارy=2استفاده کنیدواز آن نقطه بر محور xهاعمود کنید
درسته ؟
این هم یه مقاله فوق العاده خوب.پارسال کار و زندگیم شده بود رفتن دنبال انواع و اقسام این روش ها.الان از هر کدومشون یه چیزایی بلدم.یادگرفتن اینها برای سال اول و دومیا مستحبه.اما سال سومیا مخصوصا المپیادفیزیکیا و نجومیا باید حتما بلد باشن.تقریبا همه شون رو تا ترم 3 دانشگاه یادمیگیریم.زیاد هم سخت نیستند.فقط باید به مفاهیم تابع و مشتق مسلط باشید.
- ارسال ها
- 364
- لایک ها
- 183
- امتیاز
- 0
پاسخ : ریشه سوم دو
این هم یه مقاله فوق العاده خوب.پارسال کار و زندگیم شده بود رفتن دنبال انواع و اقسام این روش ها.الان از هر کدومشون یه چیزایی بلدم.یادگرفتن اینها برای سال اول و دومیا مستحبه.اما سال سومیا مخصوصا المپیادفیزیکیا و نجومیا باید حتما بلد باشن.تقریبا همه شون رو تا ترم 3 دانشگاه یادمیگیریم.زیاد هم سخت نیستند.فقط باید به مفاهیم تابع و مشتق مسلط باشید.
نوشته اصلی توسط IMO_IMC

راه من اینه :
برای نشان دادن ریشه ی سوم دو روی محور ابتدا تابع y=x^3رارسم کنیدسپس ازمقدارy=2استفاده کنیدواز آن نقطه بر محور xهاعمود کنید
درسته ؟
نه.یه مشکلی هست.ما نمی دونیم به ازای چه ایکسی مقدار تابع 2 شده.مشکل اصلی ما هم همینه.روش های تخمینی خوبی برای حل معادلات f(x)=0 وجود دارن که بهترین اونها در حد نه زیاد پیشرفته بسط تیلور و تکرار نیوتونه.
راه من اینه :
برای نشان دادن ریشه ی سوم دو روی محور ابتدا تابع y=x^3رارسم کنیدسپس ازمقدارy=2استفاده کنیدواز آن نقطه بر محور xهاعمود کنید
درسته ؟
این هم یه مقاله فوق العاده خوب.پارسال کار و زندگیم شده بود رفتن دنبال انواع و اقسام این روش ها.الان از هر کدومشون یه چیزایی بلدم.یادگرفتن اینها برای سال اول و دومیا مستحبه.اما سال سومیا مخصوصا المپیادفیزیکیا و نجومیا باید حتما بلد باشن.تقریبا همه شون رو تا ترم 3 دانشگاه یادمیگیریم.زیاد هم سخت نیستند.فقط باید به مفاهیم تابع و مشتق مسلط باشید.
پاسخ : ریشه سوم دو
من یه روشی به ذهنم رسید فقط یه بازه به ما میده واسه رسم اون مثلثی که قراره یه ضلعش ریشه سوم 2 باشه.شاید کسی بتونه این روش رو تکمیل کنه.
بین ضلعها این رابطه برقراره. a^3=b^3+c^3
اگه b=1 c=1 a^3=2 اون موقع مثلث رو ساختیم.حالا اگه اشتباه نکنم ثابت میشه یه زاویه بیشتر یا کمتر از 60 داریم(الان حوصله ندارم اثبات کنم.ولی کلا یه بازه میده)
دوستان ببینند میشه کاری کرد.
من یه روشی به ذهنم رسید فقط یه بازه به ما میده واسه رسم اون مثلثی که قراره یه ضلعش ریشه سوم 2 باشه.شاید کسی بتونه این روش رو تکمیل کنه.
بین ضلعها این رابطه برقراره. a^3=b^3+c^3
اگه b=1 c=1 a^3=2 اون موقع مثلث رو ساختیم.حالا اگه اشتباه نکنم ثابت میشه یه زاویه بیشتر یا کمتر از 60 داریم(الان حوصله ندارم اثبات کنم.ولی کلا یه بازه میده)
دوستان ببینند میشه کاری کرد.
- ارسال ها
- 364
- لایک ها
- 183
- امتیاز
- 0
پاسخ : ریشه سوم دو
آقا بذارید کلی ترین چیز ممکن را بگم. اگر صفحه را مختصات بندی کنیم و هر نقطه را یک عدد مختلط در نظر بگیریم، شرط لازم برای آنکه بتوان با خط کش و پرگار و طول 1 به این نقطه رسید این است که اولا این عدد مختلط جبری باشد، یعنی یک چند جمله ای با ضرایب صحیح وجود داشته باشد که z ریشه آن باشد، ثانیا اگر p(x) چنین چند جمله ای با درجه مینیمم باشد، آنگاه درجه p(x) ، توانی از دو باشد. تازه این شرط لازمه. مثلا برای رادیکال 2 به فورژه 3، p(x) برابر است با x^3-2. و درجه این چند جمله ای 3 است و توانی از دو نیست. بنابراین نمیتوان رادیکال 2 به فورژه 3 را رسم کرد. اثبات این قضیه هم نظریه میدانها میخواهد.
آقا بذارید کلی ترین چیز ممکن را بگم. اگر صفحه را مختصات بندی کنیم و هر نقطه را یک عدد مختلط در نظر بگیریم، شرط لازم برای آنکه بتوان با خط کش و پرگار و طول 1 به این نقطه رسید این است که اولا این عدد مختلط جبری باشد، یعنی یک چند جمله ای با ضرایب صحیح وجود داشته باشد که z ریشه آن باشد، ثانیا اگر p(x) چنین چند جمله ای با درجه مینیمم باشد، آنگاه درجه p(x) ، توانی از دو باشد. تازه این شرط لازمه. مثلا برای رادیکال 2 به فورژه 3، p(x) برابر است با x^3-2. و درجه این چند جمله ای 3 است و توانی از دو نیست. بنابراین نمیتوان رادیکال 2 به فورژه 3 را رسم کرد. اثبات این قضیه هم نظریه میدانها میخواهد.
- ارسال ها
- 107
- لایک ها
- 53
- امتیاز
- 0
پاسخ : ریشه سوم دو
ببخشید. تو ضرب و جمع فرجه ها اشتباه کردم(به جای ضرب جمع کردم )و در کل تا آخر اشتباه شد.
فقط یک سوال داشتم. ما میگیم
=x^{3}-2) که
که
=\sqrt[3]{2}^{3}-2=0) حالا اگر در جایی که مقدار
حالا اگر در جایی که مقدار
) (یا همون y ) برابر صفره بر محور x عمود کنیم چرا
(یا همون y ) برابر صفره بر محور x عمود کنیم چرا
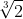 را به ما نشان نمیده؟
را به ما نشان نمیده؟
کی گفته هر زوجی را میشه؟؟ نه مثلا ریشه سوم را نمیشه، ریشه ششم را هم نمیشه. درواقع تمام ریشه هایی به شکل دو به توان n ام را فقط میشه نمایش داد. یعنی ریشه دوم، چهارم، هشتم، شانزدهم و غیره. به غیر از اینها چیز دیگری را نمیشه. اثباتش هم با میدانها است.
فقط یک سوال داشتم. ما میگیم
