سوال نظریه از نوع hard
- ارسال ها
- 327
- لایک ها
- 378
- امتیاز
- 0
پاسخ : سوال نظریه از نوع hard
ابتدا تعریف می کنیم:
}=a_n\times 2^n+a_{n-1}\times 2^{n-1}+...+a_1\times 2^1+a_0\times 2^0+b_1\times 2^{-1}+b_2\times 2^{-2}+...+b_m\times {2^{-m}}) همچنین قرار دهید
همچنین قرار دهید
=\left \lfloor n^2\alpha \right \rfloor) .
.
*فرض کنید آلفا گویا باشه و به صورت
 باشه. اونموقع
باشه. اونموقع
\in Even\:Numbers) پس نامتناهی تا
پس نامتناهی تا
 پیدا شد که
پیدا شد که
) عددی زوج بشه!
عددی زوج بشه!
*حالا فرض کنید آلفا گنگ باشه.و همچنین فرض کنید متناهی تا
) داشته باشیم که زوج باشه!میایم آلفا رو در مبنای
داشته باشیم که زوج باشه!میایم آلفا رو در مبنای
 (به صورت نامتناهی از طرف راست) مینویسیم:
(به صورت نامتناهی از طرف راست) مینویسیم:
}) اگه تعداد
اگه تعداد
 ها نامتناهی باشه اونموقع میتونیم
ها نامتناهی باشه اونموقع میتونیم
 قرار بدیم و بینهایت عدد زوج بگیریم که تناقضه! پس از یه
قرار بدیم و بینهایت عدد زوج بگیریم که تناقضه! پس از یه
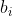 ای به بعد همه
ای به بعد همه
 ها برابر
ها برابر
 هستند! حالا یه
هستند! حالا یه
 رو در نظر بگیرید که
رو در نظر بگیرید که
 . واضحه که
. واضحه که
,P(3.2^n)) هر دو فرد هستند.
هر دو فرد هستند.
}\:(mod\:2))
\equiv \left \lfloor 2^{2n}\alpha +2^{2n+3}\alpha \right \rfloor\equiv \left \lfloor \overline{1/k_11k_21k_31...}_{(2)}+\overline{k_2/1k_31...}_{(2)} \right \rfloor\equiv \left \lfloor \overline{(k_2+1)/(k_1+1)(k_3+1)(k_2+1)(k_4+1)...} \right \rfloor\equiv 1\:(mod\:2))
/(k_1+1)(k_3+1)(k_2+1)(k_4+1)...} \right \rfloor=1 \Rightarrow k_1=k_2=k_3=k_4=...=0) چون اگر یکی از
چون اگر یکی از
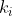 ها برابر
ها برابر
 باشد، آنگاه رقم یکان در مبنای
باشد، آنگاه رقم یکان در مبنای
 حداقل
حداقل
 میشود که تناقض است!
میشود که تناقض است!
در این حالت عدد ما، عددی گویا خواهد بود(کسر متناوب مرکب) که متناقض با فرض ما در مورد گنگ بود آلفاست!
حالت دوم:
/(k_1+1)(k_3+1)(k_2+1)(k_4+1)...} \right \rfloor=3\Rightarrow k_2=1) پس به طریق مشابه
پس به طریق مشابه
 با
با
) میتوان ثابت کرد که
میتوان ثابت کرد که
 ! پس باز هم کسر ما یک کسر متناوب مرکب خواهد شد! که متناقض با فرض گنگ بودن آلفا است!
! پس باز هم کسر ما یک کسر متناوب مرکب خواهد شد! که متناقض با فرض گنگ بودن آلفا است!
پس ثابت شد که در هر صورت بی نهایت عدد زوج در برد
) وجود دارد.
وجود دارد.
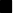
سوال( تویمادا یاکوت)
میدانیم
 ،عددی حقیقی است ثابت کنید بینهایت عدد طبیعی
،عددی حقیقی است ثابت کنید بینهایت عدد طبیعی
 وجود دارد که
وجود دارد که
 عددی زوج شود .
عددی زوج شود .
میدانیم
*فرض کنید آلفا گویا باشه و به صورت
*حالا فرض کنید آلفا گنگ باشه.و همچنین فرض کنید متناهی تا
بنابراین:
پس دوحالت داریم:
حالت اول:
حالت اول:
در این حالت عدد ما، عددی گویا خواهد بود(کسر متناوب مرکب) که متناقض با فرض ما در مورد گنگ بود آلفاست!
حالت دوم:
پس ثابت شد که در هر صورت بی نهایت عدد زوج در برد
آخرین ویرایش توسط مدیر
پاسخ : سوال نظریه از نوع hard
راه دوم:
اول ببخشید که توضیح اضافی یا کم دادم...
ثابت می کنیم حداقل یک
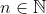 وجود دارد که
وجود دارد که
 زوج شود، و در نهایت از آن حکم را نتیجه می گیریم.
زوج شود، و در نهایت از آن حکم را نتیجه می گیریم.
برهان خلف: فرض کنید همه ی اعداد
 فرد باشند، تابع
فرد باشند، تابع
 را به این صورت تعریف می کنیم:
را به این صورت تعریف می کنیم:
) عددی صحیح نامنفی کوچکتر از
عددی صحیح نامنفی کوچکتر از
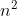 است که
است که
}{n^2}\leq&space;\{\alpha\}<&space;\frac{f(n)+1}{n^2}) . (
. (
 جزء اعشاری x است )
جزء اعشاری x است )
از تعریف تابع داریم:
\leq&space;n^2\{\alpha\}<&space;f(n)+1\Rightarrow&space;\lfloor&space;n^2\{\alpha\}&space;\rfloor=f(n)&space;\\&space;\Rightarrow&space;\{n^2\{\alpha\}\}=n^2\{\alpha\}-\lfloor&space;n^2\{\alpha\}&space;\rfloor=n^2\{\alpha\}-f(n)\\&space;\Rightarrow&space;\{n^2\{\alpha\}\}=n^2\{\alpha\}-f(n)\textbf{&space;(1)})
به راحتی می توان ثابت کرد
 . پس طبق رابطه (1) :
. پس طبق رابطه (1) :
\\&space;\Rightarrow&space;\lfloor&space;n^2\alpha&space;\rfloor=n^2\alpha-\{n^2\alpha\}=n^2\alpha-n^2\{\alpha\}+f(n)=n^2\lfloor\alpha\rfloor+f(n)&space;\\&space;\Rightarrow&space;1=\lfloor&space;n^2\alpha&space;\rfloor=n^2\lfloor\alpha\rfloor+f(n)=n^2+f(n)=n+f(n)\textrm{&space;(mod&space;2)}&space;\\&space;\Rightarrow&space;f(n)\neq&space;n\textrm{&space;(mod&space;2)}\textbf{&space;(2)})
حال فقط با استفاده از (2) به تناقض می رسیم. مجموعه های
) را به این صورت تعریف می کنیم:
را به این صورت تعریف می کنیم:
}\}) (
(
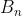 در واقع تمام مقادیری است که
در واقع تمام مقادیری است که
) می تواند اختیار کند)
می تواند اختیار کند)
)
(
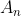 در واقع تمام مقادیری است که
در واقع تمام مقادیری است که
 می تواند اختیار کند) پس
می تواند اختیار کند) پس
) پس
پس
 و این یعنی
و این یعنی
 . فقط یک مرحله ی نسبتا زشت تا تناقض باقیمانده.
. فقط یک مرحله ی نسبتا زشت تا تناقض باقیمانده.
با محاسبات زیاد می توان نشان داد:
 پس
پس
 که تناقضه!
که تناقضه!
-----------------------------------------------------------------------------------------------------------------------------------------------
پس حداقل یک n وجود دارد، حال فرض کنید تعداد n ها متناهی باشد و تمام n هایی که
 زوج باشد عبارتند از
زوج باشد عبارتند از
 . اگر
. اگر
 که
که
 ، حکم برای
، حکم برای
 هم درست است، یعنی n طبیعی وجود دارد که
هم درست است، یعنی n طبیعی وجود دارد که
^2\alpha\rfloor=\lfloor&space;n^2\alpha'\rfloor=0\textrm{&space;(mod&space;2)}) ولی
ولی
 پس یک ضریب بزرگ تر پیدا شد که حکم برای آن درست است، تناقض!
پس یک ضریب بزرگ تر پیدا شد که حکم برای آن درست است، تناقض!
-----------------------------------------------------------------------------------------------------------------------------------------------
نکته ی مهم: طبق این راه حل
 حداقل یکی از اعداد
حداقل یکی از اعداد
 زوج است، که قویتر از حکم مسأله است.
زوج است، که قویتر از حکم مسأله است.
(با تشکر از threehandsnal عزیز!)
راه دوم:
اول ببخشید که توضیح اضافی یا کم دادم...
ثابت می کنیم حداقل یک
برهان خلف: فرض کنید همه ی اعداد
از تعریف تابع داریم:
با محاسبات زیاد می توان نشان داد:
-----------------------------------------------------------------------------------------------------------------------------------------------
پس حداقل یک n وجود دارد، حال فرض کنید تعداد n ها متناهی باشد و تمام n هایی که
-----------------------------------------------------------------------------------------------------------------------------------------------
نکته ی مهم: طبق این راه حل
(با تشکر از threehandsnal عزیز!)
آخرین ویرایش توسط مدیر
