مقایسه اعداد لگاریتمی(کمی سخت)
پاسخ : مقایسه اعداد لگاریتمی(کمی سخت)
تصادفی!! :4: ولی یک راه دیگر هم هست و اثبات با نامساوی
 هست( به وضوح اگه این نامساوی اثبات شود حکمم اثبات میشه .در اصل با این نامساوی میتوان 7 لگاریتم دیگر بین
هست( به وضوح اگه این نامساوی اثبات شود حکمم اثبات میشه .در اصل با این نامساوی میتوان 7 لگاریتم دیگر بین
 و
و
 قرار داد یعنی داریم:
قرار داد یعنی داریم:

پس حالا به عنوان سوال جدید شما نامساوی رو اثبات کنید:
سوال جدید (اثبات نامساوی):

از کجا به این رسیدین ؟:4:
پس حالا به عنوان سوال جدید شما نامساوی رو اثبات کنید:
سوال جدید (اثبات نامساوی):
پاسخ : مقایسه اعداد لگاریتمی(کمی سخت)

سلام.
توی این تاپیک می خواهیم اعداد لگاریتمی رو با هم مقایسه کنبم.
هر دو تا لگاریتمی که به نظرتون مقایسه شون سخته بذارید تا با روش های مختلف حلشون کنیم!!
تا یکی هم حل نشده سراغ بعدی نرید.
توی این تاپیک می خواهیم اعداد لگاریتمی رو با هم مقایسه کنبم.
هر دو تا لگاریتمی که به نظرتون مقایسه شون سخته بذارید تا با روش های مختلف حلشون کنیم!!
تا یکی هم حل نشده سراغ بعدی نرید.
1

در ضمن برای این که ماشین حساب به دست نگیرید لگاریتم چپی حدودا 0.04 بزرگتره.
دلیل؟؟؟
دلیل؟؟؟
پاسخ : مقایسه اعداد لگاریتمی(کمی سخت)
 و تابع
و تابع
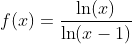 اکیدا نزولیه (x>1) (اثباتش با استفاده از مشتق). نمودار f
اکیدا نزولیه (x>1) (اثباتش با استفاده از مشتق). نمودار f
سوال جدید (اثبات نامساوی):

پاسخ : مقایسه اعداد لگاریتمی(کمی سخت)
خب الان یه روش خیلی بد و اورژانسی راجع به سوال
 به ذهنم رسید.روش استاد شریفی خیلی خیلی کوتاه و عالی بود.
به ذهنم رسید.روش استاد شریفی خیلی خیلی کوتاه و عالی بود.
روشم خیلی خیلی کلیه و اگه جایی گیر کردید حتما کمک می کنه.
میاییم و دو نقطه
and\left%20(%2039,43%20\right%20)) رو در نظر می گیریم و معادله خط گذرنده از این دو نقطه رو بدست میاریم.
رو در نظر می گیریم و معادله خط گذرنده از این دو نقطه رو بدست میاریم.

حالا کافیه ثابت کنیم
=log_{x}^{\frac{15x+17}{14}}=\frac{ln\frac{15x+17}{14}}{lnx}) به ازای x های بزرگتر از 1 اکیدا نزولیه.
به ازای x های بزرگتر از 1 اکیدا نزولیه.
=\frac{lnx^{\frac{15}{15x+17}}-ln(\frac{15x+17}{14})^{\frac{1}{x}}}{ln^2x})
^{\frac{1}{x}}}%3C%200)
^{\frac{1}{x}})
خب الان یه روش خیلی بد و اورژانسی راجع به سوال
روشم خیلی خیلی کلیه و اگه جایی گیر کردید حتما کمک می کنه.
میاییم و دو نقطه
حالا کافیه ثابت کنیم
مخرج مثبته.کافیه ثابت کنیم به ازای x های بزرگتر از 1 صورت منفیه و در نتیجه تابع اکیدا نزولیه.
کاملا واضحه که این نامساوی برقراره.چون به ازای تمامی
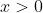 توان طرف راست بزرگتر از توان عبارت سمت چپه.
توان طرف راست بزرگتر از توان عبارت سمت چپه.
و پایه ی سمت راست به ازای
 از سمت چپ بزرگتره.
از سمت چپ بزرگتره.
پس تابع f اکیدا نزولیه و لگاریتم چپی بزرگتره!!!
و پایه ی سمت راست به ازای
پس تابع f اکیدا نزولیه و لگاریتم چپی بزرگتره!!!
پاسخ : مقایسه اعداد لگاریتمی(کمی سخت)
این سوال رو من قبلا ثابت کردم.
http://www.irysc.com/forum/t4623-6/#post70468
تصادفی!! :4: ولی یک راه دیگر هم هست و اثبات با نامساوی
 هست( به وضوح اگه این نامساوی اثبات شود حکمم اثبات میشه .در اصل با این نامساوی میتوان 7 لگاریتم دیگر بین
هست( به وضوح اگه این نامساوی اثبات شود حکمم اثبات میشه .در اصل با این نامساوی میتوان 7 لگاریتم دیگر بین
 و
و
 قرار داد یعنی داریم:
قرار داد یعنی داریم:

پس حالا به عنوان سوال جدید شما نامساوی رو اثبات کنید:
سوال جدید (اثبات نامساوی):

پس حالا به عنوان سوال جدید شما نامساوی رو اثبات کنید:
سوال جدید (اثبات نامساوی):
http://www.irysc.com/forum/t4623-6/#post70468
- ارسال ها
- 1,326
- لایک ها
- 998
- امتیاز
- 113
پاسخ : مقایسه اعداد لگاریتمی(کمی سخت)
متوجه نمیشم.
ببین تو صفحه ای که یک محورش a و یکیش b باشه خم هایی که loga b ثایت رو نشون میده خط نیست.یک خم لگاریتمیه.
هر خم ماله یک F ثابته.یک مقدار برای لگ آ ب.این خم ها هم بسته نیستند ولی ربع صفحه بالا رو میکنند دو بخش:بالایی که F های بزرگتره.و پایینی که F های کوچکتره.
پس باید ثابت کنیم که نقطه ما بالای خم (نه خط) میافته یا نه.
خب الان یه روش خیلی بد و اورژانسی راجع به سوال
 به ذهنم رسید.روش استاد شریفی خیلی خیلی کوتاه و عالی بود.
به ذهنم رسید.روش استاد شریفی خیلی خیلی کوتاه و عالی بود.
روشم خیلی خیلی کلیه و اگه جایی گیر کردید حتما کمک می کنه.
میاییم و دو نقطه
and\left%20(%2039,43%20\right%20)) رو در نظر می گیریم و معادله خط گذرنده از این دو نقطه رو بدست میاریم.
رو در نظر می گیریم و معادله خط گذرنده از این دو نقطه رو بدست میاریم.

حالا کافیه ثابت کنیم
=log_{x}^{\frac{15x+17}{14}}=\frac{ln\frac{15x+17}{14}}{lnx}) به ازای x های بزرگتر از 1 اکیدا نزولیه.
به ازای x های بزرگتر از 1 اکیدا نزولیه.
=\frac{lnx^{\frac{15}{15x+17}}-ln(\frac{15x+17}{14})^{\frac{1}{x}}}{ln^2x})
^{\frac{1}{x}}}%3C%200)
^{\frac{1}{x}})
روشم خیلی خیلی کلیه و اگه جایی گیر کردید حتما کمک می کنه.
میاییم و دو نقطه
حالا کافیه ثابت کنیم
مخرج مثبته.کافیه ثابت کنیم به ازای x های بزرگتر از 1 صورت منفیه و در نتیجه تابع اکیدا نزولیه.
کاملا واضحه که این نامساوی برقراره.چون به ازای تمامی
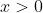 توان طرف راست بزرگتر از توان عبارت سمت چپه.
توان طرف راست بزرگتر از توان عبارت سمت چپه.
و پایه ی سمت راست به ازای
 از سمت چپ بزرگتره.
از سمت چپ بزرگتره.
پس تابع f اکیدا نزولیه و لگاریتم چپی بزرگتره!!!
و پایه ی سمت راست به ازای
پس تابع f اکیدا نزولیه و لگاریتم چپی بزرگتره!!!
ببین تو صفحه ای که یک محورش a و یکیش b باشه خم هایی که loga b ثایت رو نشون میده خط نیست.یک خم لگاریتمیه.
هر خم ماله یک F ثابته.یک مقدار برای لگ آ ب.این خم ها هم بسته نیستند ولی ربع صفحه بالا رو میکنند دو بخش:بالایی که F های بزرگتره.و پایینی که F های کوچکتره.
پس باید ثابت کنیم که نقطه ما بالای خم (نه خط) میافته یا نه.
پاسخ : مقایسه اعداد لگاریتمی(کمی سخت)
کلا هدفم رو از این کار میگم.
بی نهایت تا نمودار لگاریتمی میشه تعریف کرد که از دو نقطه
 بگذرند. حالا یکی از این نمودار ها
بگذرند. حالا یکی از این نمودار ها
=log_{x}^{\frac{15x+17}{14}}=\frac{ln\frac{15x+17}{14}}{lnx}) هستش.این نمودار رو انتخاب کردم چون ساده ترین نمودار برای ادامه
هستش.این نمودار رو انتخاب کردم چون ساده ترین نمودار برای ادامه
راه حله.
یه روش دیگه هم اینه.
میاییم و مثلا نقطه ی لگاریتم 50 تو مبنای 44 رو در نظر میگیرم.حالا از سه نقطه متمایز یک و تنها یک تابع لگاریتمی که عبارت جلوش سهمی درجه 2 هستش میگذره.حالا بین پایه و عبارت جلوی لگاریتم یه رابطه درجه 2 برقراره و ادامه اثبات سخت تر میشه.
متوجه نمیشم.
ببین تو صفحه ای که یک محورش a و یکیش b باشه خم هایی که loga b ثایت رو نشون میده خط نیست.یک خم لگاریتمیه.
هر خم ماله یک F ثابته.یک مقدار برای لگ آ ب.این خم ها هم بسته نیستند ولی ربع صفحه بالا رو میکنند دو بخش:بالایی که F های بزرگتره.و پایینی که F های کوچکتره.
پس باید ثابت کنیم که نقطه ما بالای خم (نه خط) میافته یا نه.
ببین تو صفحه ای که یک محورش a و یکیش b باشه خم هایی که loga b ثایت رو نشون میده خط نیست.یک خم لگاریتمیه.
هر خم ماله یک F ثابته.یک مقدار برای لگ آ ب.این خم ها هم بسته نیستند ولی ربع صفحه بالا رو میکنند دو بخش:بالایی که F های بزرگتره.و پایینی که F های کوچکتره.
پس باید ثابت کنیم که نقطه ما بالای خم (نه خط) میافته یا نه.
بی نهایت تا نمودار لگاریتمی میشه تعریف کرد که از دو نقطه
راه حله.
یه روش دیگه هم اینه.
میاییم و مثلا نقطه ی لگاریتم 50 تو مبنای 44 رو در نظر میگیرم.حالا از سه نقطه متمایز یک و تنها یک تابع لگاریتمی که عبارت جلوش سهمی درجه 2 هستش میگذره.حالا بین پایه و عبارت جلوی لگاریتم یه رابطه درجه 2 برقراره و ادامه اثبات سخت تر میشه.
- ارسال ها
- 1,326
- لایک ها
- 998
- امتیاز
- 113
پاسخ : مقایسه اعداد لگاریتمی(کمی سخت)
یعنی چی!!بی نهایت نمودار میشه تعریف کرد.ولی که چی!؟؟!!
باید هدف داشته باشیم از این کار!!
فقط باید ثابت کنیم اون نقطه هه بالای منحنی F=const میافته یا نه.
و اون منحنی فقط یک دونه است.فقط یک دونه!!هر نقطه توی صفحه یک F هست.F=loga b .حالا به ازای هر F یک خم داریم.یعنی یک سری a و b ها میتونیم داشته باشیم که F همشون بشه یک مقداری(F).
پس نمیشه هر منحنی دلمون خاست انتخاب کنیم!
راهتو باید درست کنی...باید استدلال کنی چون اون خم F=const تقعر رو به پایین داره..اگر از خط بینشون بالا باشیم..حتمن از خم F ثابت هم بالاییم.
کلا هدفم رو از این کار میگم.
بی نهایت تا نمودار لگاریتمی میشه تعریف کرد که از دو نقطه
 بگذرند. حالا یکی از این نمودار ها
بگذرند. حالا یکی از این نمودار ها
=log_{x}^{\frac{15x+17}{14}}=\frac{ln\frac{15x+17}{14}}{lnx}) هستش.این نمودار رو انتخاب کردم چون ساده ترین نمودار برای ادامه
هستش.این نمودار رو انتخاب کردم چون ساده ترین نمودار برای ادامه
راه حله.
یه روش دیگه هم اینه.
میاییم و مثلا نقطه ی لگاریتم 50 تو مبنای 44 رو در نظر میگیرم.حالا از سه نقطه متمایز یک و تنها یک تابع لگاریتمی که عبارت جلوش سهمی درجه 2 هستش میگذره.حالا بین پایه و عبارت جلوی لگاریتم یه رابطه درجه 2 برقراره و ادامه اثبات سخت تر میشه.
بی نهایت تا نمودار لگاریتمی میشه تعریف کرد که از دو نقطه
راه حله.
یه روش دیگه هم اینه.
میاییم و مثلا نقطه ی لگاریتم 50 تو مبنای 44 رو در نظر میگیرم.حالا از سه نقطه متمایز یک و تنها یک تابع لگاریتمی که عبارت جلوش سهمی درجه 2 هستش میگذره.حالا بین پایه و عبارت جلوی لگاریتم یه رابطه درجه 2 برقراره و ادامه اثبات سخت تر میشه.
باید هدف داشته باشیم از این کار!!
فقط باید ثابت کنیم اون نقطه هه بالای منحنی F=const میافته یا نه.
و اون منحنی فقط یک دونه است.فقط یک دونه!!هر نقطه توی صفحه یک F هست.F=loga b .حالا به ازای هر F یک خم داریم.یعنی یک سری a و b ها میتونیم داشته باشیم که F همشون بشه یک مقداری(F).
پس نمیشه هر منحنی دلمون خاست انتخاب کنیم!
راهتو باید درست کنی...باید استدلال کنی چون اون خم F=const تقعر رو به پایین داره..اگر از خط بینشون بالا باشیم..حتمن از خم F ثابت هم بالاییم.
پاسخ : مقایسه اعداد لگاریتمی(کمی سخت)
فهمیدم مشکلت چیه.
با اونجا که گفتم خط بین این دو نقطه مشکل داشتی.
باید میگفتم تنها رابطه درجه 1 برقرار بین این دو نقطه.
من اصلا از این که خط واصل بین دو نقطه
 هیچ استفاده ای توی حل نکردما!!!
هیچ استفاده ای توی حل نکردما!!!
هدفم رو بذار بهتر بگم.
اومدم یه منحنی انتخاب کردم که از این دو نقطه بگذره.
بعد ثابت کردم این منحنی اکیدا نزولیه.
چون فرم منحنی ام جوری بود که از اکیدا نزولی بودنش میشد نتیجه گرفت یکی از اون دو نقطه عرض پایین تری داره نسبت به دیگری پس سوال حل شد
یعنی چی!!بی نهایت نمودار میشه تعریف کرد.ولی که چی!؟؟!!
باید هدف داشته باشیم از این کار!!
فقط باید ثابت کنیم اون نقطه هه بالای منحنی F=const میافته یا نه.
و اون منحنی فقط یک دونه است.فقط یک دونه!!هر نقطه توی صفحه یک F هست.F=loga b .حالا به ازای هر F یک خم داریم.یعنی یک سری a و b ها میتونیم داشته باشیم که F همشون بشه یک مقداری(F).
پس نمیشه هر منحنی دلمون خاست انتخاب کنیم!
راهتو باید درست کنی...باید استدلال کنی چون اون خم F=const تقعر رو به پایین داره..اگر از خط بینشون بالا باشیم..حتمن از خم F ثابت هم بالاییم.
باید هدف داشته باشیم از این کار!!
فقط باید ثابت کنیم اون نقطه هه بالای منحنی F=const میافته یا نه.
و اون منحنی فقط یک دونه است.فقط یک دونه!!هر نقطه توی صفحه یک F هست.F=loga b .حالا به ازای هر F یک خم داریم.یعنی یک سری a و b ها میتونیم داشته باشیم که F همشون بشه یک مقداری(F).
پس نمیشه هر منحنی دلمون خاست انتخاب کنیم!
راهتو باید درست کنی...باید استدلال کنی چون اون خم F=const تقعر رو به پایین داره..اگر از خط بینشون بالا باشیم..حتمن از خم F ثابت هم بالاییم.
با اونجا که گفتم خط بین این دو نقطه مشکل داشتی.
باید میگفتم تنها رابطه درجه 1 برقرار بین این دو نقطه.
من اصلا از این که خط واصل بین دو نقطه
هدفم رو بذار بهتر بگم.
اومدم یه منحنی انتخاب کردم که از این دو نقطه بگذره.
بعد ثابت کردم این منحنی اکیدا نزولیه.
چون فرم منحنی ام جوری بود که از اکیدا نزولی بودنش میشد نتیجه گرفت یکی از اون دو نقطه عرض پایین تری داره نسبت به دیگری پس سوال حل شد
پاسخ : مقایسه اعداد لگاریتمی(کمی سخت)
نه!!!
خب نکته همینه که من بین a وb یه رابطه درجه 1 پیدا کردم و حالا داریم
=log_{x}^{\frac{15x+17}{14}}=\frac{ln\frac{15x+17}{14}}{lnx})
مگه نموداری که کشیدی محوراش a , b نیست؟
و ما میخوایم loga b رو حساب کنیم؟
و ما میخوایم loga b رو حساب کنیم؟
نه!!!
خب نکته همینه که من بین a وb یه رابطه درجه 1 پیدا کردم و حالا داریم
رو رسم می کنیم که یه رابطه بین x و y هستش.در ضمن برای راحتی a رو کردم x .
یه بار دیگه با دقت این رو بخون کاملا توضیح دادم چکار کردم.
--------------------------------------------------------------------
هدفم رو بذار بهتر بگم.
اومدم یه منحنی انتخاب کردم که از این دو نقطه بگذره.
بعد ثابت کردم این منحنی اکیدا نزولیه.
چون فرم منحنی ام جوری بود که از اکیدا نزولی بودنش میشد نتیجه گرفت یکی از اون دو نقطه عرض پایین تری داره نسبت به دیگری پس سوال حل شد
یه بار دیگه با دقت این رو بخون کاملا توضیح دادم چکار کردم.
--------------------------------------------------------------------
هدفم رو بذار بهتر بگم.
اومدم یه منحنی انتخاب کردم که از این دو نقطه بگذره.
بعد ثابت کردم این منحنی اکیدا نزولیه.
چون فرم منحنی ام جوری بود که از اکیدا نزولی بودنش میشد نتیجه گرفت یکی از اون دو نقطه عرض پایین تری داره نسبت به دیگری پس سوال حل شد
