خب من سوالای سال اولو میذارم و لطفا دوستان دوم و سومی که شرکت کردن هم سوالاشونو اینجا بذارن تا روی سوالات بحث کنیم:
1- نقطه
 درون متوازی الاضلاع
درون متوازی الاضلاع
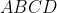 انتخاب می شود به طوری که
انتخاب می شود به طوری که
 . ثابت کنید پاره خط
. ثابت کنید پاره خط
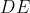 بر پاره خطی که وسط پاره خط
بر پاره خطی که وسط پاره خط
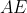 را به وسط پاره خط
را به وسط پاره خط
 وصل می کند عمود است. (4 امتیاز)
وصل می کند عمود است. (4 امتیاز)
2- یک منطقه حفاظت شده به شکل یک چند ضلعی غیر محدب است. این منطقه با یک حصار شفاف در طول محیطش محافظت می شود و در یک میدان مین احاطه شده است به گونه ای که یک جاسوس تنها می تواند در طول حصار حرکت کند. جاسوس یک بار دور منطقه حرکت میکند به طوری که منطقه همیشه در سمت راست اوست. یک خط مستقیم برق با 36 دکل این منطقه را قطع می کند که برخی از دکل ها درون منطقه و برخی بیرون از آن قرار دارند. خط برق از رئوس حصار عبور نمی کند. جاسوس هر بار که از خط برق عبور می کند تعداد دکل های سمت چپ خود را می شمارد (او می تواند همه ی دکل ها را ببیند). جاسوس به محض بازگشت به نقطه اولیه در مجموع 2015 دکل را شمرده است. تعداد دکل های درون حصار چند تا است؟ (6 امتیاز)
3- الف) اعداد صحیح مثبت
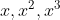 با رقم یکسانی شروع می شوند. آیا می توان نتیجه گرفت این رقم برابر یک است؟ (3 امتیاز)
با رقم یکسانی شروع می شوند. آیا می توان نتیجه گرفت این رقم برابر یک است؟ (3 امتیاز)
ب) همین سوال را برای اعداد
 جواب دهید. (4 امتیاز)
جواب دهید. (4 امتیاز)
4- برای هر ضلع یک چند ضلعی خط شامل آن ضلع حداقل از یک راس دیگر این چند ضلعی عبور می کند. آیا ممکن است که تعداد رئوس این چند ضلعی،
الف) بیشتر از 9 نباشد؟ (4 امتیاز)
ب) بیشتر از 8 نباشد؟ (5 امتیاز)
5- الف) یک جدول
 (که
(که
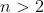 ) با اعداد به گونه ای پر شده است که جمع اعداد در همه ستون ها متفاوت است. ثابت کنید می توان اعداد را در جدول طوری جابجا کرد که جمع اعداد در همه ستون ها همچنان متفاوت باشد و علاوه بر آن جمع اعداد در همه سطر ها نیز متفاوت باشد. (3 امتیاز)
) با اعداد به گونه ای پر شده است که جمع اعداد در همه ستون ها متفاوت است. ثابت کنید می توان اعداد را در جدول طوری جابجا کرد که جمع اعداد در همه ستون ها همچنان متفاوت باشد و علاوه بر آن جمع اعداد در همه سطر ها نیز متفاوت باشد. (3 امتیاز)
ب) یک جدول
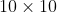 با اعداد به گونه ای پر شده است که جمع اعداد در همه ستون ها متفاوت است. آیا همواره می توان اعداد را در جدول طوری جابجا کرد که جمع اعداد در همه ستون ها همچنان متفاوت باشد و علاوه بر آن جمع اعداد در همه سطر ها نیز متفاوت باشد؟ (6 امتیاز)
با اعداد به گونه ای پر شده است که جمع اعداد در همه ستون ها متفاوت است. آیا همواره می توان اعداد را در جدول طوری جابجا کرد که جمع اعداد در همه ستون ها همچنان متفاوت باشد و علاوه بر آن جمع اعداد در همه سطر ها نیز متفاوت باشد؟ (6 امتیاز)
6- یک
 ضلعی محدب با اضلاع برابر درون یک دایره واقع شده است. هر ضلع در هر دو جهت تا محل برخورد با دایره امتداد داده شده است به طوری که دو پاره خط در بیرون چند ضلعی تشکیل می دهد. ثابت کنید می توان این
ضلعی محدب با اضلاع برابر درون یک دایره واقع شده است. هر ضلع در هر دو جهت تا محل برخورد با دایره امتداد داده شده است به طوری که دو پاره خط در بیرون چند ضلعی تشکیل می دهد. ثابت کنید می توان این
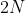 پاره خط به وجود آمده را به دو دسته تقسیم کرد که مجموع طول پاره خط ها در دو دسته برابر باشد. (9 امتیاز)
پاره خط به وجود آمده را به دو دسته تقسیم کرد که مجموع طول پاره خط ها در دو دسته برابر باشد. (9 امتیاز)
7- پادشاهی 2015 جادوگر دارد . تعدادی از جادوگر ها خوب و تعدادی از آن ها بد هستند. اما پادشاه خوب یا بد بودن آن ها را نمی داند ولی هر جادوگر می داند کدام جادوگر خوب و کدام بد است! هر جادوگر خوب همواره راست می گوید اما جادوگر دروغ گو هم می تواند راست بگوید و هم دروغ! پادشاه تعدادی کارت را آماده می کند که روی هر کدام سوالی نوشته شده که می تواند برای جادوگرهای مختلف متفاوت باشد اما جواب جادوگر ها به سوالات فقط می تواند بله یا خیر باشد. بعد از این که پادشاه به پاسخ جادوگر ها گوش داد می تواند یکی از جادوگر ها را از دری جادویی بیرون کند. هنگامی که جادوگر ها از در جادویی خارج می شوند مشخص می شود که این جادوگر خوب است یا بد! و دوباره پادشاه سوالات دیگری را از جادوگر های دیگر می پرسد. سوال ها می تواند مشابه یا متفاوت باشد. در هر مرحله پادشاه می تواند جادوگری را از در اخراج کند و هم می تواند اخراج نکند. ثابت کنید پادشاه می تواند همه ی جادوگرهای بد را اخراج کند در حالی که حداکثر یک جادوگر خوب اخراج شود. (10 امتیاز)
1- نقطه
2- یک منطقه حفاظت شده به شکل یک چند ضلعی غیر محدب است. این منطقه با یک حصار شفاف در طول محیطش محافظت می شود و در یک میدان مین احاطه شده است به گونه ای که یک جاسوس تنها می تواند در طول حصار حرکت کند. جاسوس یک بار دور منطقه حرکت میکند به طوری که منطقه همیشه در سمت راست اوست. یک خط مستقیم برق با 36 دکل این منطقه را قطع می کند که برخی از دکل ها درون منطقه و برخی بیرون از آن قرار دارند. خط برق از رئوس حصار عبور نمی کند. جاسوس هر بار که از خط برق عبور می کند تعداد دکل های سمت چپ خود را می شمارد (او می تواند همه ی دکل ها را ببیند). جاسوس به محض بازگشت به نقطه اولیه در مجموع 2015 دکل را شمرده است. تعداد دکل های درون حصار چند تا است؟ (6 امتیاز)
3- الف) اعداد صحیح مثبت
ب) همین سوال را برای اعداد
4- برای هر ضلع یک چند ضلعی خط شامل آن ضلع حداقل از یک راس دیگر این چند ضلعی عبور می کند. آیا ممکن است که تعداد رئوس این چند ضلعی،
الف) بیشتر از 9 نباشد؟ (4 امتیاز)
ب) بیشتر از 8 نباشد؟ (5 امتیاز)
5- الف) یک جدول
ب) یک جدول
6- یک
7- پادشاهی 2015 جادوگر دارد . تعدادی از جادوگر ها خوب و تعدادی از آن ها بد هستند. اما پادشاه خوب یا بد بودن آن ها را نمی داند ولی هر جادوگر می داند کدام جادوگر خوب و کدام بد است! هر جادوگر خوب همواره راست می گوید اما جادوگر دروغ گو هم می تواند راست بگوید و هم دروغ! پادشاه تعدادی کارت را آماده می کند که روی هر کدام سوالی نوشته شده که می تواند برای جادوگرهای مختلف متفاوت باشد اما جواب جادوگر ها به سوالات فقط می تواند بله یا خیر باشد. بعد از این که پادشاه به پاسخ جادوگر ها گوش داد می تواند یکی از جادوگر ها را از دری جادویی بیرون کند. هنگامی که جادوگر ها از در جادویی خارج می شوند مشخص می شود که این جادوگر خوب است یا بد! و دوباره پادشاه سوالات دیگری را از جادوگر های دیگر می پرسد. سوال ها می تواند مشابه یا متفاوت باشد. در هر مرحله پادشاه می تواند جادوگری را از در اخراج کند و هم می تواند اخراج نکند. ثابت کنید پادشاه می تواند همه ی جادوگرهای بد را اخراج کند در حالی که حداکثر یک جادوگر خوب اخراج شود. (10 امتیاز)

