ماراتن المپیاد ریاضی- کاری از دوره طلا
- شروع کننده موضوع goldeneagle
- تاریخ شروع
- برچسپ ها استفاده اعداد طبیعی المپیاد المپیاد ریاضی المپیادهای علمی ایران ریاضی ریشه سوال طبیعی عدد طبیعی قضیه قوانین ماراتن مربع معادله نظریه اعداد همکاری هندسه پیشرفته یک سوال
- ارسال ها
- 327
- لایک ها
- 378
- امتیاز
- 0
پاسخ : ماراتن المپیاد ریاضی- کاری از دوره طلا
من سوال شما رو ندیدم.داشتم سوال
^2) رو حل میکردم.اگه جایگذاری کنین و یخورده ور برین (و البته اگه من جوب نزده باشم) جواب
رو حل میکردم.اگه جایگذاری کنین و یخورده ور برین (و البته اگه من جوب نزده باشم) جواب
^2+1,t^2+1)) درسته. البته من چیزی رو کپی نکردم.اگه کپی کرده بودم که هیچوقت نمیتونست جوابم غلط دربیاد. در ضمن من الان دوباره سوالو از اول حل میکنم که اگه جوبی داشت برطرف کنم و اگه راه حلم غلط بوده باشه اطلاع میدم بهتون که غلطه و اگه درست بوده باشه که راه حلم در مورد اون تیکه ای که از مینیمال بودن x نتیجه شد که فقط حالت k=2 درسته رو هم براتون توضیح میدم.
درسته. البته من چیزی رو کپی نکردم.اگه کپی کرده بودم که هیچوقت نمیتونست جوابم غلط دربیاد. در ضمن من الان دوباره سوالو از اول حل میکنم که اگه جوبی داشت برطرف کنم و اگه راه حلم غلط بوده باشه اطلاع میدم بهتون که غلطه و اگه درست بوده باشه که راه حلم در مورد اون تیکه ای که از مینیمال بودن x نتیجه شد که فقط حالت k=2 درسته رو هم براتون توضیح میدم.
در ضمن-ما اومدیم اینجا که المپیاد بخونیم و در کنار همدیگه سوال حل کنیم.فک نکنم دلیلی برای من که سال سومم باشه که بخوام یه سوال قشنگ رو بپیچونم!!
:21:
اون که جواب یه سوال دیگست.
توی حل سوال قبلی که من هیچ جایی ندیدم نوشته باشن
^2+1,t^2+1)) هم جوابه. :lol: پس امکان داره این یکی هم جوب داشته باشه.
هم جوابه. :lol: پس امکان داره این یکی هم جوب داشته باشه.
خب اگه قرار باشه هر سوالی که از vieta jumping میدن یه چیزایی رو کپی کنید که دیگه نمیشه راه حل.
ضمن این که من توی راه حل شما در سوال قبلی هم نفهمیدم چطوری از مینیمال بودن x نتیجه گرفتید که
 .
.
PS: من خودم همیشه جور دیگه ای از این تکنیک استفاده می کنم.
ولی اگه می خواین برای این که ماراتن راه بیفته این سوال رو بچونیم من حرفی ندارم.(هر چند هنوز حل نشده!)
اون که جواب یه سوال دیگست.
توی حل سوال قبلی که من هیچ جایی ندیدم نوشته باشن
خب اگه قرار باشه هر سوالی که از vieta jumping میدن یه چیزایی رو کپی کنید که دیگه نمیشه راه حل.
ضمن این که من توی راه حل شما در سوال قبلی هم نفهمیدم چطوری از مینیمال بودن x نتیجه گرفتید که
PS: من خودم همیشه جور دیگه ای از این تکنیک استفاده می کنم.
ولی اگه می خواین برای این که ماراتن راه بیفته این سوال رو بچونیم من حرفی ندارم.(هر چند هنوز حل نشده!)
من سوال شما رو ندیدم.داشتم سوال
در ضمن-ما اومدیم اینجا که المپیاد بخونیم و در کنار همدیگه سوال حل کنیم.فک نکنم دلیلی برای من که سال سومم باشه که بخوام یه سوال قشنگ رو بپیچونم!!
- ارسال ها
- 327
- لایک ها
- 378
- امتیاز
- 0
پاسخ : ماراتن المپیاد ریاضی- کاری از دوره طلا
احساس میکنم راه حلم تا حد زیادی جوب داشت که واسه همین از اول حل کردم سوال رو با یه راه حل دیگه که امیدوارم درست باشه:
\Rightarrow mn-1|(m+n-1)^2)
^2}{mn-1})
:m^2-m(kn-2n+2)+(n-1)^2+k=0)
+(y-1)^2+k=0)
+(y-1)^2+k=0)
-x+2=\frac{(y-1)^2+k}{x }\geq x\Rightarrow k\geq (x-y+1)(x+y-1))
\Rightarrow \frac{(x+y-1)^2}{xy-1}\geq 2(x+y-1)\Rightarrow 2x\geq x+y\geq \: \geq 2xy-1\Rightarrow 2x(y-1)\leq 1\Rightarrow x(y-1)=0\Rightarrow x=2,y=1\Rightarrow k=4)
^2\Rightarrow x^2-1|4x-5\Rightarrow x^2-1\leq 4x-5\Rightarrow (x-2)^2\leq \: \leq 0\Rightarrow x=y=2 \Rightarrow k=3)
^2+(n-2)^2+(m-n)^2=0\: \Rightarrow m=n=2)
^2-2(m+n)+5=0)
^2+1\\ n=p^2+1 \end{matrix}\right.)
=((p+1)^2+1,p^2+1))
|x=(p+1)^2+1,y=p^2+1\: \: (p\in \mathbb{Z}) \right \}\bigcup \left \{ (2,2) \right \})
همه ی
) های طبیعی را بیابید که :
های طبیعی را بیابید که :
^2)
احساس میکنم راه حلم تا حد زیادی جوب داشت که واسه همین از اول حل کردم سوال رو با یه راه حل دیگه که امیدوارم درست باشه:
با به هنگ mn-1 بردن به این نتیجه میرسیم که:
حال باید تمامی مقادیر k را بیابیم:
حال فرض کنید از بین جواب هایی که مولفه دومشان مینیمال است؛آن جوابی را انتخاب کنیم که مولفه اولش از همه کوچکتر است.فرض کنید این جواب
) باشد بنابراین داریم:
باشد بنابراین داریم:
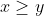 .بنابراین خواهیم داشت:
.بنابراین خواهیم داشت:
حال ریشه دوم این معادله بر حسب x را
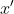 فرض میکنیم. بنابراین:
فرض میکنیم. بنابراین:
داریم
 . طبق ویت داریم:
. طبق ویت داریم:
حال دو حالت را بررسی میکنیم:
بنابراین
 است. بنابراین این دو حالت را بررسی می کنیم:
است. بنابراین این دو حالت را بررسی می کنیم:
چون m-n عددی فرد است قرار دهید :
)
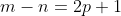 .بنابراین خواهیم داشت:
.بنابراین خواهیم داشت:
بنابراین مجموعه جواب این میشه:
آخرین ویرایش توسط مدیر
پاسخ : ماراتن المپیاد ریاضی- کاری از دوره طلا
این هم سوالی که راه حلش کامل گذاشته نشده بود:
همه
 های طبیعی که
های طبیعی که
 .
.
داریم
 .
.
ادعا می کنیم :
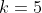
بدون کم شدن از کلیت مساله فرض کنید
 . در بین همه ی زوج های
. در بین همه ی زوج های
 که در شرایط مساله صدق می کنند
که در شرایط مساله صدق می کنند
 را طوری اختیار می کنیم که
را طوری اختیار می کنیم که
 حداقل باشد. در واقع
حداقل باشد. در واقع
 ریشه های چندجمله ای
ریشه های چندجمله ای
 هستند. توجه کنید که در این صورت
هستند. توجه کنید که در این صورت
 هم ریشه های چند جمله ای مذکور هستند و چون
هم ریشه های چند جمله ای مذکور هستند و چون
 حداقل است پس داریم :
حداقل است پس داریم :


و چون فرض مان بر این بود که
 پس به ازای
پس به ازای
 نامنفی داریم :
نامنفی داریم :
 .
.
اکنون با جاگذاری در معادله ی اول بدست می آوریم :

با تعیین علامت بر حسب
 داریم :
داریم :
 .
.
پس
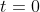 یا
یا
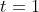 .
.
اگر
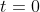 داریم
داریم
 که تناقض است.
که تناقض است.
پس
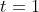 یعنی
یعنی

اکنون باید تمام جواب های طبیعی معادله ی
 را بیابیم :4: (فکر کنم خود این به تنهایی یک سوال بوده- TST ویتنام!)
را بیابیم :4: (فکر کنم خود این به تنهایی یک سوال بوده- TST ویتنام!)
دقت کنید اگر
 ریشه های آن باشند آنگاه
ریشه های آن باشند آنگاه
 هم ریشه های آن هستند. جواب اولیه مان هم
هم ریشه های آن هستند. جواب اولیه مان هم
 هست. پس جمله عمومی مان هم
هست. پس جمله عمومی مان هم
 است، باشرط
است، باشرط
 .
.
پس کل جواب ها به فرم
 به دست می آید.
به دست می آید.
امیدوارم از 7 نمره همشو بگیرم :4:
این هم سوالی که راه حلش کامل گذاشته نشده بود:
همه
داریم
ادعا می کنیم :
بدون کم شدن از کلیت مساله فرض کنید
و چون فرض مان بر این بود که
اکنون با جاگذاری در معادله ی اول بدست می آوریم :
با تعیین علامت بر حسب
پس
اگر
پس
اکنون باید تمام جواب های طبیعی معادله ی
دقت کنید اگر
پس کل جواب ها به فرم
امیدوارم از 7 نمره همشو بگیرم :4:
- ارسال ها
- 327
- لایک ها
- 378
- امتیاز
- 0
پاسخ : ماراتن المپیاد ریاضی- کاری از دوره طلا
این سوال به نسبت سوالای قبلتون یخورده آسونتر بود.اینم راه حلش:
+(n^2+k)=0)
+(y^2+k)=0)
 (x+y)\leq \: \leq 2x)


\leq y(x-y)(x+y)\leq 2x\Rightarrow 0< y^2\leq x(1-y)\Rightarrow y=1\Rightarrow x-1|x^2+1\Rightarrow x-1|2\: ,\: x\geq y+2\Rightarrow x=3\Rightarrow k=5)
:m^2-5mn+n^2-5=0)

.\left ( \frac{5+\sqrt{21}}{2} \right )^n+\left ( \frac{13+3\sqrt{21}}{2\sqrt{21}} \right ).\left ( \frac{5-\sqrt{21}}{2} \right )^n)
|x=a_n,y=a_{n+1} \right \}\bigcup \left \{ (y,x)|x=a_n,y=a_{n+1} \right \})
همه زوج های
) از اعداد طبیعی رو بیابید که
از اعداد طبیعی رو بیابید که
 .
.
راه حل این سوال رو هم تمیز و مرتب بنویسین که بریم سوال بعد :4:
راه حل این سوال رو هم تمیز و مرتب بنویسین که بریم سوال بعد :4:
حال مثل سوال قبل فرض کنید از بین جواب هایی که مولفه دومشان مینیمال است؛آن جوابی را انتخاب کنیم که مولفه اولش از همه کوچکتر است.فرض کنید این جواب
) باشد بنابراین داریم:
باشد بنابراین داریم:
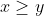 .بنابراین خواهیم داشت:
.بنابراین خواهیم داشت:
حال فرض کنید جواب دیگر این معادله
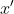 باشد.و طبق فرض داریم
باشد.و طبق فرض داریم
 . بنابراین طبق ویت خواهیم داشت:
. بنابراین طبق ویت خواهیم داشت:
حال سه حالت را در نظر میگیریم:
که جواب طبیعی ندارد.
بنابراین سوال به حل این معادله دیوفانتی تبدیل شد که جواب مینیمال آن
) است.
است.
واضح است که از
=0) میتوان به
میتوان به
=0) رسید. بنابراین به این دنباله بازگشتی خواهیم رسید:
رسید. بنابراین به این دنباله بازگشتی خواهیم رسید:
بنابراین کلیه جوابها به این فرم خواهند بود:
{نوشتن جوابها با math-sina همزمان شدند}
آخرین ویرایش توسط مدیر
پاسخ : ماراتن المپیاد ریاضی- کاری از دوره طلا
جناب math-sina, اگه اون دنباله بازگشتی رو هم حل کنید خیلی بهتره, البته جوابا به فرم رادیکالی میشن ولی اگه فرم کلی جوابو بنویسین دیگه مطمئنین نمره از دست نمیدین :3:
جناب threehandsnal, شما هم فکر کنم توی اون بخش که دنباله بازگشتی رو حل کردین یه توان n کم گذاشتین. :3:
ممنون از جوابایی که نوشتین. من نتونستم غلطی توش پیدا کنم. (البته به علت خواب آلودگی حال نداشتم محاسباتتونو چک کنم, ولی ایشالله که درسته, چون کلیت راه حل درست بود)
سوال آخر رو هم به زودی علیرضا میذاره.
جناب math-sina, اگه اون دنباله بازگشتی رو هم حل کنید خیلی بهتره, البته جوابا به فرم رادیکالی میشن ولی اگه فرم کلی جوابو بنویسین دیگه مطمئنین نمره از دست نمیدین :3:
جناب threehandsnal, شما هم فکر کنم توی اون بخش که دنباله بازگشتی رو حل کردین یه توان n کم گذاشتین. :3:
ممنون از جوابایی که نوشتین. من نتونستم غلطی توش پیدا کنم. (البته به علت خواب آلودگی حال نداشتم محاسباتتونو چک کنم, ولی ایشالله که درسته, چون کلیت راه حل درست بود)
سوال آخر رو هم به زودی علیرضا میذاره.
- ارسال ها
- 327
- لایک ها
- 378
- امتیاز
- 0
پاسخ : ماراتن المپیاد ریاضی- کاری از دوره طلا
با اجازه همگی من توی Maths Links به جوابای اینجا پست دادم =))
با اجازه همگی من توی Maths Links به جوابای اینجا پست دادم =))
AoPS Forum - two vieta jumping problems • Art of Problem Solving
(Post #3)
AoPS Forum - Diophantine equation at romanian tst • Art of Problem Solving
(Post #11)
AoPS Forum - x^2 + y^2 - 5xy + 5 = 0 • Art of Problem Solving
(Post #10)
(Post #3)
AoPS Forum - Diophantine equation at romanian tst • Art of Problem Solving
(Post #11)
AoPS Forum - x^2 + y^2 - 5xy + 5 = 0 • Art of Problem Solving
(Post #10)
دیگه بلد نبودن زبان فارسی رو google translate باید بهشون کمک کنه :دی
پاسخ : ماراتن المپیاد ریاضی- کاری از دوره طلا
به قول آقای شریفی طرف مثلا از چین با کلی ادعا و کلی سابقه اومده تو AoPs ! بعدش مجبوره بیاد نوشته های بچه دبیرستانی های ایرانو بخونه !!
با اجازه همگی من توی Maths Links به جوابای اینجا پست دادم =))
AoPS Forum - two vieta jumping problems • Art of Problem Solving
(Post #3)
AoPS Forum - Diophantine equation at romanian tst • Art of Problem Solving
(Post #11)
AoPS Forum - x^2 + y^2 - 5xy + 5 = 0 • Art of Problem Solving
(Post #10)
(Post #3)
AoPS Forum - Diophantine equation at romanian tst • Art of Problem Solving
(Post #11)
AoPS Forum - x^2 + y^2 - 5xy + 5 = 0 • Art of Problem Solving
(Post #10)
دیگه بلد نبودن زبان فارسی رو google translate باید بهشون کمک کنه :دی
- ارسال ها
- 48
- لایک ها
- 173
- امتیاز
- 0
- ارسال ها
- 327
- لایک ها
- 378
- امتیاز
- 0
پاسخ : ماراتن المپیاد ریاضی- کاری از دوره طلا
اول از همه یه تشکر درست حسابی از goldeneagle عزیز که این سوالو گذاشتن و این وقت شب مارو شب زنده دار نگه داشتن البته اون نکته یا راهنمایی آخر کارتون منو خیلی دلگرم کرد برای حل مساله :21:
البته اون نکته یا راهنمایی آخر کارتون منو خیلی دلگرم کرد برای حل مساله :21:
حل کردم و امیدوارم جوب نزده باشم این وقت شب جوب خور هممون بالاست
این وقت شب جوب خور هممون بالاست 
ابتدا با یذره ساده کردن جمله عمومی دنباله بازگشتی و جمع کردن طرفین با 1 این شکلی میشه:
(a_{k-1}+1)=a_k^2+1\Rightarrow \left\{\begin{matrix} a_k+1|a_{k-1}^2+1\\ a_{k-1}+1|a_k^2+1 \end{matrix}\right.)

(a_{k+1}+1)\Rightarrow 2t(a_{k+1}+1)\equiv 2(mod \: 4))



(k+1)=m^2+1)
(k+1)\equiv 1(mod\: 4)\Rightarrow (k+1,4)=1)
^2+1\Rightarrow n+1|(n^2-k)^2+(k+1)^2\Rightarrow n+1|(k-1)^2+(k+1)^2\Rightarrow n+1|2(k^2+1),(n+1,2)=1\Rightarrow n+1|k^2+1)

^2)
(a_3+1)\\ a_3^2+1=(a_2+1)(a_4+1) \end{matrix}\right.)

(a_3+1)\Rightarrow (a_1+1)(2s+1+1)\equiv 2(mod\: 8)\Rightarrow (a_1+1)(k+1)\equiv \: \equiv 1(mod\: 4)\Rightarrow (a_1+1,4)=1)
\Rightarrow 3|a_2^2+1\Rightarrow 3|1)


 بنامیم آنگاه خواهیم داشت:
بنامیم آنگاه خواهیم داشت:

سوال خیلی قشنگی بود.بازم دم این چهار تا طلایی گرم که از این سوالای باحال میذارن
دیگه صبح شده.ما شب زنده دارا بگیریم بخوابیم
سوال آخر برای شب زنده دارها: IMO Shortlist 2009
همه ی اعداد طبیعی n را بیابید که دنباله ی
 از اعداد طبیعی موجود باشد که
از اعداد طبیعی موجود باشد که
 برای هر
برای هر

یک نکته: یک چیزی توی این سواله خیلی نامردیه!!!! شب بر شما خوش! :4:
همه ی اعداد طبیعی n را بیابید که دنباله ی
یک نکته: یک چیزی توی این سواله خیلی نامردیه!!!! شب بر شما خوش! :4:
اول از همه یه تشکر درست حسابی از goldeneagle عزیز که این سوالو گذاشتن و این وقت شب مارو شب زنده دار نگه داشتن
حل کردم و امیدوارم جوب نزده باشم
ابتدا با یذره ساده کردن جمله عمومی دنباله بازگشتی و جمع کردن طرفین با 1 این شکلی میشه:
حالا میخوایم ثابت کنیم که
 زوج اند.برهان خلف: فرض کنید مثلا
زوج اند.برهان خلف: فرض کنید مثلا
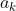 فرد باشه.داریم:
فرد باشه.داریم:
بنابراین
 هم فرد هست.
هم فرد هست.
پس
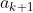 زوجه!ولی داریم:
زوجه!ولی داریم:
که تناقض است.با فرض اینکه
 هم فرده به طور مشابه به تناقض میرسیم.بنابراین داریم(k هایی را میتوانیم در نظر بگیریم که در اشتراک راه طی شده برای اثبات زوج بودن
هم فرده به طور مشابه به تناقض میرسیم.بنابراین داریم(k هایی را میتوانیم در نظر بگیریم که در اشتراک راه طی شده برای اثبات زوج بودن
 هستند) :
هستند) :
حال برای ساده سازی در نوشتن فرض کنید
 .بنابراین داریم:
.بنابراین داریم:
حال فرض کنید از تمامی جوابهای طبیعی و زوج این معادله جوابی را در نظر بگیریم که در آن
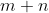 مینیمال باشد.
مینیمال باشد.
بنابراین k زوج است.
پس توانستیم از جواب (m,n) به جواب (n,k) برسیم و چون
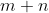 مینیمال است پس فقط سه حالت داریم:
مینیمال است پس فقط سه حالت داریم:
1)
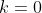 .یعنی:
.یعنی:
1)
که این با زوج بودن n متناقض است.پس این حالت رد شد.
2)
 .یعنی:
.یعنی:
2)
که هیچ جواب طبیعی ای ندارد.
3)
 .یعنی اینکه از روی هر دو
.یعنی اینکه از روی هر دو
) میتوانیم نامتناهی تا جمله دیگر با m+n بزرگتر مثل
میتوانیم نامتناهی تا جمله دیگر با m+n بزرگتر مثل
) بسازیم و از آنجا که تعداد مقسوم علیه های
بسازیم و از آنجا که تعداد مقسوم علیه های
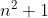 متناهی است ولی با توجه به فرض داریم
متناهی است ولی با توجه به فرض داریم
 و این یعنی تناقض!!!
و این یعنی تناقض!!!
و این یعنی هیچ جواب زوج و طبیعی
) ای وجود ندارد که
ای وجود ندارد که
 .
.
حال باید n ای را بیابیم که هیچ دو عضو متوالی و زوجی از آن رابطه
 را نداشته باشند.حال ثابت میکنیم حداکثر طول دنباله n=4 است.فرض کنید طول دنباله ای 5 باشد.که اگر در معادلات بالا قرار دهیم k=3 آنگاه به این نتیجه میرسیم که
را نداشته باشند.حال ثابت میکنیم حداکثر طول دنباله n=4 است.فرض کنید طول دنباله ای 5 باشد.که اگر در معادلات بالا قرار دهیم k=3 آنگاه به این نتیجه میرسیم که
 هر دو زوج هستند!و با توجه به معادلات بالا به تناقض میرسیم!!!(چون همانطور که گفته شد این معادله بالا به ازای m,n زوج جواب ندارد.پس دنباله به طول 3 خواهد شد!!)بنابراین جمله پنجمی وجود ندارد و پس
هر دو زوج هستند!و با توجه به معادلات بالا به تناقض میرسیم!!!(چون همانطور که گفته شد این معادله بالا به ازای m,n زوج جواب ندارد.پس دنباله به طول 3 خواهد شد!!)بنابراین جمله پنجمی وجود ندارد و پس
 است.حال دنباله ای با طول 4 میسازیم!
است.حال دنباله ای با طول 4 میسازیم!
میدانیم در دنباله ای به طول 4 داریم:
3)
و این یعنی هیچ جواب زوج و طبیعی
حال باید n ای را بیابیم که هیچ دو عضو متوالی و زوجی از آن رابطه
میدانیم در دنباله ای به طول 4 داریم:
برای اینکه بتوانیم حدسی برای ساخت دنباله بدست بیاوریم باید داشته باشیم:
میدانیم که
 همزمان نباید زوج باشند!اگر
همزمان نباید زوج باشند!اگر
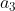 فرد باشد آنگاه
فرد باشد آنگاه
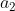 نیز فرد خواهد بود.سعی میکنیم با همین حدس فرد بود هر دوی اینها جلو برویم.
نیز فرد خواهد بود.سعی میکنیم با همین حدس فرد بود هر دوی اینها جلو برویم.
بنابراین
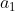 زوج خواهد شد.از مقادیر ابتدایی شروع میکنیم.
زوج خواهد شد.از مقادیر ابتدایی شروع میکنیم.
که تناقض است!
حال با امتحان کردن
 و بدست آوردن بقیه جملات دنباله,اولین
و بدست آوردن بقیه جملات دنباله,اولین
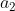 قابل قبولی که بدست می آید(
قابل قبولی که بدست می آید(
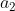 ای که جملات
ای که جملات
 طبیعی باشند)
طبیعی باشند)
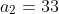 است.پس این دنباله به صورت زیر است:
است.پس این دنباله به صورت زیر است:
این دنباله بدست آمده کوچکترین دنباله است(و از 1384 اش برمیاد که سوال پیشنهادی جهانی ایران توی(2005 میلادی=1384 خورشیدی) IMO 2005 باشه ایران از این خز بازیا ممکنه در بیاره
ایران از این خز بازیا ممکنه در بیاره )
)
البته واضحه وقتی برای n=4 دنباله ساخته شده با حذف کردن جمله 4 ام این دنباله؛دنباله ای برای n=3 ساخته میشود و با حذف دو جمله آخر دنباله ای برای n=2 و با حذف سه جمله آخر دنباله ای برای n=1 ساخته میشود که در جمله عمومی دنباله نیز صدق میکند...پس اگر مجموعه جواب را
سوال خیلی قشنگی بود.بازم دم این چهار تا طلایی گرم که از این سوالای باحال میذارن
دیگه صبح شده.ما شب زنده دارا بگیریم بخوابیم
آخرین ویرایش توسط مدیر
پاسخ : ماراتن المپیاد ریاضی- کاری از دوره طلا
 ,
,
 ,در نتیجه
,در نتیجه
 ,
,
/a_{k-1}+1 \right )^{2} -a_{k-1}^{2})
^{2}+1-2\left ( a_{k-1}+1 \right )\left ( a_{k}^{2}+1)-a_{k-1}^{2}\left ( a_{k-1}+1 \right ))
حال نتیجه میگیریم با اندکی محاسبات که
^{2}+1-2\left ( a_{k-1}+1 \right )\left ( a_{k}^{2}+1)-a_{k-1}^{2}\left ( a_{k-1}+1 \right )) , حالا بازهم محاسبات را خلاصه تر میکنم و نتیجه میگیرم که
, حالا بازهم محاسبات را خلاصه تر میکنم و نتیجه میگیرم که
 ,حالا طبق داشته های قبلی میدانیم که
,حالا طبق داشته های قبلی میدانیم که
 و همچنین
و همچنین
 این را از رابطه بالا با ساده سازی بدست میآوریم پس حالا
این را از رابطه بالا با ساده سازی بدست میآوریم پس حالا
 با ساده سازی روایطی که بر حسب
با ساده سازی روایطی که بر حسب
 و
و
 مجموعه ی جواب بدست می آِد
مجموعه ی جواب بدست می آِد

البته به تمام معنا شرمنده ه خیلی خیلی خلاصه نوشتم ولی مطمئنم اشتباه محاسباتی نداشتم
ببخشید که دومین پاسخ رو دادم خوب شما شبا بی خوابی به سرتون میزنه به من چه :90:
سوال آخر برای شب زنده دارها: IMO Shortlist 2009
همه ی اعداد طبیعی n را بیابید که دنباله ی
 از اعداد طبیعی موجود باشد که
از اعداد طبیعی موجود باشد که
 برای هر
برای هر

یک نکته: یک چیزی توی این سواله خیلی نامردیه!!!! شب بر شما خوش! :4:
همه ی اعداد طبیعی n را بیابید که دنباله ی
یک نکته: یک چیزی توی این سواله خیلی نامردیه!!!! شب بر شما خوش! :4:
حال نتیجه میگیریم با اندکی محاسبات که
البته به تمام معنا شرمنده ه خیلی خیلی خلاصه نوشتم ولی مطمئنم اشتباه محاسباتی نداشتم
ببخشید که دومین پاسخ رو دادم خوب شما شبا بی خوابی به سرتون میزنه به من چه :90:
آخرین ویرایش توسط مدیر
- ارسال ها
- 48
- لایک ها
- 173
- امتیاز
- 0
پاسخ : ماراتن المپیاد ریاضی- کاری از دوره طلا
میدونید منظورم از نامردی این بود که برای n=4 مثالش خیلی بی خوده....اگه این سوال مثالش این قدر بی خود نبود خیلی بهتر میشد (شاید اصلا میرفت توی سوالات IMO)....تو هر چه قدرم تلاش کنی بازم باید (3و7و13و17و23و27و33) را چک کنی که بدون ماشین حساب سر جلسه واقعا اعصاب خورد کنه! مضافا بر این که چون مثال n=4 ساده نیست امکان داره فکر کنیم که n=4 مثال داره و کلا از مسیر اثبات پرت شیم بیرون...نامردیه دیگه!
میدونید منظورم از نامردی این بود که برای n=4 مثالش خیلی بی خوده....اگه این سوال مثالش این قدر بی خود نبود خیلی بهتر میشد (شاید اصلا میرفت توی سوالات IMO)....تو هر چه قدرم تلاش کنی بازم باید (3و7و13و17و23و27و33) را چک کنی که بدون ماشین حساب سر جلسه واقعا اعصاب خورد کنه! مضافا بر این که چون مثال n=4 ساده نیست امکان داره فکر کنیم که n=4 مثال داره و کلا از مسیر اثبات پرت شیم بیرون...نامردیه دیگه!
- ارسال ها
- 327
- لایک ها
- 378
- امتیاز
- 0
پاسخ : ماراتن المپیاد ریاضی- کاری از دوره طلا
آره خوب :3: ولی نه وقتی آدم تو خونه اس و میتونه محاسبات رو یواشکی با ماشین حساب انجام بده :78::65:
میدونید منظورم از نامردی این بود که برای n=4 مثالش خیلی بی خوده....اگه این سوال مثالش این قدر بی خود نبود خیلی بهتر میشد (شاید اصلا میرفت توی سوالات imo)....تو هر چه قدرم تلاش کنی بازم باید (3و7و13و17و23و27و33) را چک کنی که بدون ماشین حساب سر جلسه واقعا اعصاب خورد کنه! مضافا بر این که چون مثال n=4 ساده نیست امکان داره فکر کنیم که n=4 مثال داره و کلا از مسیر اثبات پرت شیم بیرون...نامردیه دیگه!
آخرین ویرایش توسط مدیر
