ماراتن المپیاد ریاضی- کاری از دوره طلا
- شروع کننده موضوع goldeneagle
- تاریخ شروع
- برچسپ ها استفاده اعداد طبیعی المپیاد المپیاد ریاضی المپیادهای علمی ایران ریاضی ریشه سوال طبیعی عدد طبیعی قضیه قوانین ماراتن مربع معادله نظریه اعداد همکاری هندسه پیشرفته یک سوال
پاسخ : ماراتن المپیاد ریاضی- کاری از دوره طلا
من خودم از آقای احمدپور پرسیدم بهترین منبع هندسه مختلط روComplex numbers from A to Z دونستن و همچنین استاد شکریان اینو تایید کردن ببخشید که من دخالت کردم دی
من خودم از آقای احمدپور پرسیدم بهترین منبع هندسه مختلط روComplex numbers from A to Z دونستن و همچنین استاد شکریان اینو تایید کردن ببخشید که من دخالت کردم دی
آخرین ویرایش توسط مدیر
- ارسال ها
- 327
- لایک ها
- 378
- امتیاز
- 0
پاسخ : ماراتن المپیاد ریاضی- کاری از دوره طلا
نمیدونم ولی من شنیدم که خود خانم مینا دلیر روی فرد سوال 6 جهانی رو با هندسه اعداد مختلط ثابت کردن(http://www.imo-official.org/participant_r.aspx?id=20908).اینم لینک جواب ایشونه فک کنم:
شنیدم آقای افتخاری سوال 6 جهانی پارسالو با مختلط حل کردن که راه حل شون 6 صفحه (شایدم 8 صفحه !) شده بود !
آخرین ویرایش توسط مدیر
- ارسال ها
- 327
- لایک ها
- 378
- امتیاز
- 0
پاسخ : ماراتن المپیاد ریاضی- کاری از دوره طلا
عدد مختلط - ویکیپدیا
Complex number - Wikipedia, the free encyclopedia
این ۲ تا لینک رو یه نگاهی بندازید تا با خود عدد مختلط آشنا بشید ، ضرب و جمع شون جدید نیست ولی مفهوم ضرب تو اعداد مختلط خیلی قابل لمس تره چون نتیجهاش یه تجانس مارپیچ خواهد بود .
فقط در حد تعریف هم بلد باشید کافیه . تا ظهر چند تا مساله ساده از مختلط میذارم بعد سوالش رو سخت تر میکنیم !
عدد مختلط - ویکیپدیا
Complex number - Wikipedia, the free encyclopedia
این ۲ تا لینک رو یه نگاهی بندازید تا با خود عدد مختلط آشنا بشید ، ضرب و جمع شون جدید نیست ولی مفهوم ضرب تو اعداد مختلط خیلی قابل لمس تره چون نتیجهاش یه تجانس مارپیچ خواهد بود .
فقط در حد تعریف هم بلد باشید کافیه . تا ظهر چند تا مساله ساده از مختلط میذارم بعد سوالش رو سخت تر میکنیم !
- ارسال ها
- 48
- لایک ها
- 173
- امتیاز
- 0
پاسخ : ماراتن المپیاد ریاضی- کاری از دوره طلا
به سینا: مگه شوکی(shoiki) هستند ایشون که 6 صفحه راه حل بنویسیند؟ :4:
به threehandsnal : نخیر راه حل ایشون به هندسه مختلط هیچ ربطی نداشت....:3: نکته بامزه و نامفهوم برای من اینجاست که این خبرها چه جوری تولید می شوند ؟! (بیخیال ..جمع کنیم این بحثها رو)
به ماهان : تو ساعت 4:11 PM پست دادی ...چه جوری تا ظهر چند تا سوال می ذاری؟ نکنه منظورت فرداس؟!! :4: یا من اشتباه استدلال می کنم؟ :39:
به سینا: مگه شوکی(shoiki) هستند ایشون که 6 صفحه راه حل بنویسیند؟ :4:
به threehandsnal : نخیر راه حل ایشون به هندسه مختلط هیچ ربطی نداشت....:3: نکته بامزه و نامفهوم برای من اینجاست که این خبرها چه جوری تولید می شوند ؟! (بیخیال ..جمع کنیم این بحثها رو)
به ماهان : تو ساعت 4:11 PM پست دادی ...چه جوری تا ظهر چند تا سوال می ذاری؟ نکنه منظورت فرداس؟!! :4: یا من اشتباه استدلال می کنم؟ :39:
آخرین ویرایش توسط مدیر
- ارسال ها
- 327
- لایک ها
- 378
- امتیاز
- 0
پاسخ : ماراتن المپیاد ریاضی- کاری از دوره طلا
من خودم داشتم وب گردی میکردم که یهو دیدم نوشته جواب سوال 6 جهانی با اعداد مختلط.زیرشم نوشته بود خانم دلیر روی فرد هم مثل این راه رو حل کردن.آدرس سایته یادم نیست.ولی احتمالا یذره سایت خسته ای بود که از این خبرا داد :d
به threehandsnal : نخیر راه حل ایشون به هندسه مختلط هیچ ربطی نداشت....:3: نکته بامزه و نامفهوم برای من اینجاست که این خبرها چه جوری تولید می شوند ؟! (بیخیال ..جمع کنیم این بحثها رو)
پاسخ : ماراتن المپیاد ریاضی- کاری از دوره طلا
محل طلاقی اون چهار خط رو مبدا صفحه ی مختلط می گیریم. عدد متناظر با رئوس رو هم با حروف کوچک نمایش می دهیم. نقاط وسط اضلاع هم میانگین دو سر اون ضلع هستند. داریم از اونجایی که مثلا وسط ab با d و مبدا همخط اند پس حاصل تقسیم a+b/2 بر d عددی حقیقی است. یعنی حاصل جمعa/d و b/d عددی حقیقی است که یعنی Im(a/d)=-Im(b/d و روابط مشابهی داریم برای سایر اضلاع و از طرفی برای هر دو عدد مختلط a,b داریم Im(a/b)=(-|a|[SUP]2[/SUP]/|b|[SUP]2[/SUP])Im(b/a از روی این دو لم نتیجه می شود
Im(e/c)=-Im(a/c) =(|a|[SUP]2[/SUP]/|c|[SUP]2[/SUP])Im(c/a)=(-|a|[SUP]2[/SUP]/|c|[SUP]2[/SUP])Im(d/a)=(|d|[SUP]2[/SUP]/|c|[SUP]2[/SUP])Im(a/d)=(-|d|[SUP]2[/SUP]/|c|[SUP]2[/SUP])Im(b/d)=(|b|[SUP]2[/SUP]/|c|[SUP]2[/SUP])Im(d/b)=(-|b|[SUP]2[/SUP]/|c|[SUP]2[/SUP])Im(e/b
=-Im(\frac{a}{c}) = Im (\frac{c}{a})\cdot (\frac{|a|^{2}}{|c|^{2}})= Im (\frac{d}{a})\cdot (\frac{-|a|^{2}}{|c|^{2}})= Im (\frac{a}{d})\cdot (\frac{|d|^{2}}{|c|^{2}})= Im (\frac{b}{d})\cdot (\frac{-|d|^{2}}{|c|^{2}})= Im (\frac{d}{b})\cdot (\frac{|b|^{2}}{|c|^{2}})= Im (\frac{e}{b})\cdot (\frac{-|b|^{2}}{|c|^{2}}))
اگر در تساوی بالا به اولین و آخرین عبارت نگاه کنید می بینید که نتیجه می ده Im(b/e)=-Im(c/e که نتیجه می ده حاصل تقسیم b+c بر e حقیقی است که حکم را نتیجه می دهد.
معذرت می خوام یکم بد نوشتم. امیدوارم محاسباتم درست باشه.
محل طلاقی اون چهار خط رو مبدا صفحه ی مختلط می گیریم. عدد متناظر با رئوس رو هم با حروف کوچک نمایش می دهیم. نقاط وسط اضلاع هم میانگین دو سر اون ضلع هستند. داریم از اونجایی که مثلا وسط ab با d و مبدا همخط اند پس حاصل تقسیم a+b/2 بر d عددی حقیقی است. یعنی حاصل جمعa/d و b/d عددی حقیقی است که یعنی Im(a/d)=-Im(b/d و روابط مشابهی داریم برای سایر اضلاع و از طرفی برای هر دو عدد مختلط a,b داریم Im(a/b)=(-|a|[SUP]2[/SUP]/|b|[SUP]2[/SUP])Im(b/a از روی این دو لم نتیجه می شود
Im(e/c)=-Im(a/c) =(|a|[SUP]2[/SUP]/|c|[SUP]2[/SUP])Im(c/a)=(-|a|[SUP]2[/SUP]/|c|[SUP]2[/SUP])Im(d/a)=(|d|[SUP]2[/SUP]/|c|[SUP]2[/SUP])Im(a/d)=(-|d|[SUP]2[/SUP]/|c|[SUP]2[/SUP])Im(b/d)=(|b|[SUP]2[/SUP]/|c|[SUP]2[/SUP])Im(d/b)=(-|b|[SUP]2[/SUP]/|c|[SUP]2[/SUP])Im(e/b
اگر در تساوی بالا به اولین و آخرین عبارت نگاه کنید می بینید که نتیجه می ده Im(b/e)=-Im(c/e که نتیجه می ده حاصل تقسیم b+c بر e حقیقی است که حکم را نتیجه می دهد.
معذرت می خوام یکم بد نوشتم. امیدوارم محاسباتم درست باشه.
آخرین ویرایش توسط مدیر
پاسخ : ماراتن المپیاد ریاضی- کاری از دوره طلا
مرسی ، راه حلتون درسته . اینجا هم میتونید سوال و راه حلی که گذاشتم رو ببینید . چند تا کار که تو این مساله انجام دادیم و مهم هستند :
۱-منتقل کردن شکل به یه جایی که مبدا مختصات بیاد رو نقطهای که راه حل رو ساده تر کنه . مثلا اینجا بدیهی بود که نقطه تلاقی باید نقطه ویژهای باشه .
۲-مفهوم هم خط بودن با مرکز مختصات تو اعداد مختلط
۳- فرض کنید ۲ تا نقطه a,b روی دایره واحد باشند در این صورت :
وسط وتر ab میشه میانگین حسابی a,b
وسط کمان ab میشه میانگین هندسی a,b
قطب ab میشه میانگین توافقی a,b
(منظور از قطب ،محل تلاقی مماسهای بر دایره در نقاط a,b است)
مساله اولی که گذاشتم از یه جهت خاص بود ، مرکز مختصات توش مهم بود ولی خود دایره واحد توش موثر نبود . در صورتی که در بیشتر مسائل شما باید یه دایره (که معمولاً یکتا تعیین میشه!) رو انتخاب کنید و روی اون کار کنید . تو مساله بعدی شما با یه دایره هم سر و کار دارید .
سوال بعد :
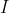 مرکز چهار ضلعی محیطی
مرکز چهار ضلعی محیطی
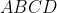 است . این دایره محاطی در
است . این دایره محاطی در
 بر
بر
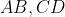 مماس است .
مماس است .
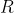 محل طلاقی
محل طلاقی
 . عمود بر
. عمود بر
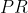 در
در

 را در
را در
 قطع میکند . عمود بر
قطع میکند . عمود بر
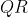 در
در

 را در
را در
 قطع میکند . ثابت کنید
قطع میکند . ثابت کنید

مرسی ، راه حلتون درسته . اینجا هم میتونید سوال و راه حلی که گذاشتم رو ببینید . چند تا کار که تو این مساله انجام دادیم و مهم هستند :
۱-منتقل کردن شکل به یه جایی که مبدا مختصات بیاد رو نقطهای که راه حل رو ساده تر کنه . مثلا اینجا بدیهی بود که نقطه تلاقی باید نقطه ویژهای باشه .
۲-مفهوم هم خط بودن با مرکز مختصات تو اعداد مختلط
۳- فرض کنید ۲ تا نقطه a,b روی دایره واحد باشند در این صورت :
وسط وتر ab میشه میانگین حسابی a,b
وسط کمان ab میشه میانگین هندسی a,b
قطب ab میشه میانگین توافقی a,b
(منظور از قطب ،محل تلاقی مماسهای بر دایره در نقاط a,b است)
مساله اولی که گذاشتم از یه جهت خاص بود ، مرکز مختصات توش مهم بود ولی خود دایره واحد توش موثر نبود . در صورتی که در بیشتر مسائل شما باید یه دایره (که معمولاً یکتا تعیین میشه!) رو انتخاب کنید و روی اون کار کنید . تو مساله بعدی شما با یه دایره هم سر و کار دارید .
سوال بعد :
آخرین ویرایش توسط مدیر
پاسخ : ماراتن المپیاد ریاضی- کاری از دوره طلا
اول تشکر می کنم بابت زحماتتون و مخصوصا بابت این سوال جالب.:3:
سعی می کنیم b0 رو حساب کنیم. دو تا خط داریم که می دونیم b0 روی اونهاست. اولا می دونیم b0 با مرکز مختصات و Bهمخطه پس

حالا از اونجایی که RPبرRB[SUB]0[/SUB] عموده داریم

}{2a-b-d})
حالا از اینجا b[SUB]0[/SUB] بدست می آد.
}{d-b})
به طور مشابه c[SUB]0[/SUB] حساب میشه.
}{d-b})
حالا مقدار نرم c[SUB]0[/SUB]b[SUB]0[/SUB] حساب می کنیم.
(\bar{c_{0}}-\bar{b_{0}})=(\frac{2b(d-a)}{d-b}-\frac{2b(d-c)}{d-b})(\frac{2\frac{1}{b}(\frac{1}{d}-\frac{1}{a})}{\frac{1}{d}-\frac{1}{b}}-\frac{2\frac{1}{b}(\frac{1}{d}-\frac{1}{c})}{\frac{1}{d}-\frac{1}{b}})=-4(\frac{\frac{a}{c}+\frac{c}{a}-2}{(d-b)(\frac{1}{d}-\frac{1}{b})}))
با توجه به اینکه عبارت بالا نسبت به aوc و همچنین نسبت به b وd متقارنه بنابراین مقدار نرم a[SUB]0[/SUB]d[SUB]0[/SUB] هم همین میشه که حکم رو نتیجه می ده. امیدوارم محاسباتم درست باشه.
به علاوه من یه سوال از اساتید طلایی دارم. خوب مثلا وقتی ما این سوالو ببینیم چطور بفهمیم با مختلط خوب حل میشه.:39: اگه مقدار b0 پیچیده میشد طبیعتا خیلی کار سخت و حتی غیر ممکن میشد . اینجا شانس اوردیم که b0 خوب محاسبه شد. یعنی تو یک کلام خواستم بپرسم چه سوالایی مختلط خورشون ملسه. با تشکر از زحماتتون
اول تشکر می کنم بابت زحماتتون و مخصوصا بابت این سوال جالب.:3:
سعی می کنیم b0 رو حساب کنیم. دو تا خط داریم که می دونیم b0 روی اونهاست. اولا می دونیم b0 با مرکز مختصات و Bهمخطه پس
حالا از اونجایی که RPبرRB[SUB]0[/SUB] عموده داریم
حالا از اینجا b[SUB]0[/SUB] بدست می آد.
به طور مشابه c[SUB]0[/SUB] حساب میشه.
حالا مقدار نرم c[SUB]0[/SUB]b[SUB]0[/SUB] حساب می کنیم.
با توجه به اینکه عبارت بالا نسبت به aوc و همچنین نسبت به b وd متقارنه بنابراین مقدار نرم a[SUB]0[/SUB]d[SUB]0[/SUB] هم همین میشه که حکم رو نتیجه می ده. امیدوارم محاسباتم درست باشه.
به علاوه من یه سوال از اساتید طلایی دارم. خوب مثلا وقتی ما این سوالو ببینیم چطور بفهمیم با مختلط خوب حل میشه.:39: اگه مقدار b0 پیچیده میشد طبیعتا خیلی کار سخت و حتی غیر ممکن میشد . اینجا شانس اوردیم که b0 خوب محاسبه شد. یعنی تو یک کلام خواستم بپرسم چه سوالایی مختلط خورشون ملسه. با تشکر از زحماتتون
پاسخ : ماراتن المپیاد ریاضی- کاری از دوره طلا
اولا یه معذرت خواهی باید بکنم به خاطر این همه تاخیر ، همونطور که گودرز گفت این روزا یه خورده اوضاعم به هم ریختست .ولی سعی میکنم هر شب سر بزنم :
"شبا که تو میخوابی آقا ماهان بیداره --- تو خوابه خوش میبینی ، ماهان سوال میذاره !"
اینم لینک مساله قبلی
راه حل "Louis" برای من یکی راه حل سر راستی نبود . در صورتی که حل مختلطش کمتر از ۵ دقیقه وقت گرفت . نظر شما چیه ؟
سوال بعدی :
در مثلث حاده الزاویه
 داریم
داریم
 . دوایر محیطی
. دوایر محیطی
 اضلاع
اضلاع
 رو به ترتیب برای بار دوم در
رو به ترتیب برای بار دوم در
 قطع میکنند . ثابت کنید مرکز دایره محیطی
قطع میکنند . ثابت کنید مرکز دایره محیطی
 روی خط اویلر
روی خط اویلر
 قرار دارد .
قرار دارد .
(
 مرکز ارتفاعی)
مرکز ارتفاعی)
اولا یه معذرت خواهی باید بکنم به خاطر این همه تاخیر ، همونطور که گودرز گفت این روزا یه خورده اوضاعم به هم ریختست .ولی سعی میکنم هر شب سر بزنم :
"شبا که تو میخوابی آقا ماهان بیداره --- تو خوابه خوش میبینی ، ماهان سوال میذاره !"
اینم لینک مساله قبلی
راه حل "Louis" برای من یکی راه حل سر راستی نبود . در صورتی که حل مختلطش کمتر از ۵ دقیقه وقت گرفت . نظر شما چیه ؟
سوال بعدی :
در مثلث حاده الزاویه
(
آخرین ویرایش توسط مدیر




