ماراتن جبر (سطح پیشرفته)
Aref گفت
یعنی بقیه ی متغیر ها کوچکتر از یک میشن. و این یعنی
به یه نتیجه ی خوب رسید. لزومی نداره که یه نابرابری خوش فرم رو بشه از اون اول به کار برد. ولی میشه با توجه به جواب معادله (که قابل حدس زدنه) یه کارهایی انجام داد.
دستگاه جدید به صورت
[center:f92d5c6ed1]

[center:f92d5c6ed1]
در می آید. با توجه به برابری مقادیر سمت راست معادله ها، اگر
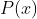 یک چندجمله ای از درجه ی حداکثر 2 باشد،
یک چندجمله ای از درجه ی حداکثر 2 باشد،

چراکه مجموع ضرایب چندجمله ای
 برابر صفر است (توی این سیگما و سیگمای بعد، منظور از
برابر صفر است (توی این سیگما و سیگمای بعد، منظور از
 ، همون
، همون
 هستش). بنابراین
هستش). بنابراین

اما با توجه به فرض مسئله،
 . بنابراین
. بنابراین
 . با جایگذاری این مقادیر در معادله نهایتا به جواب
. با جایگذاری این مقادیر در معادله نهایتا به جواب
 می رسیم.
می رسیم.
[/center:f92d5c6ed1]
M_Sharifi گفت
[center:bfdf0731c3]
با توجه به برابری مقادیر سمت راست معادله ها، اگر
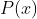 یک چندجمله ای از درجه ی حداکثر 2 باشد،
یک چندجمله ای از درجه ی حداکثر 2 باشد،

چراکه مجموع ضرایب چندجمله ای
 برابر صفر است
برابر صفر است
[/center:bfdf0731c3]
Aref گفت
M_Sharifi گفت
[center:102d274448]
با توجه به برابری مقادیر سمت راست معادله ها، اگر
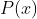 یک چندجمله ای از درجه ی حداکثر 2 باشد،
یک چندجمله ای از درجه ی حداکثر 2 باشد،

چراکه مجموع ضرایب چندجمله ای
 برابر صفر است
برابر صفر است
[/center:102d274448]
mousavi گفت
پایه استقرا مشخصه
a_n<=1/2n ^1/2
می خواهیم ثابت کنیم
a_n/1+a_n^2<=1/2 * n+1 ^1/2
اگر ساده کنیم
a_n^2 *2n <=a_n^4 +1
n- a_n^2 ^2 -n^2 +1 >=0
عبارت فوق بزرگتر است از
n -1/4n^2 ^2 -n^2 +1
که این هم مثبت است(توجه کنید در بالا از شرط a_n>0 استفاده کردیم)
a_n<=1/2n ^1/2
می خواهیم ثابت کنیم
a_n/1+a_n^2<=1/2 * n+1 ^1/2
اگر ساده کنیم
a_n^2 *2n <=a_n^4 +1
n- a_n^2 ^2 -n^2 +1 >=0
عبارت فوق بزرگتر است از
n -1/4n^2 ^2 -n^2 +1
که این هم مثبت است(توجه کنید در بالا از شرط a_n>0 استفاده کردیم)
