ماراتن جبر

math1998 · 1393/6/15

سلام دوستان با عذر خواهی و عرض معذرت جناب اقای math ولی همونطور که میدونید ماراتن های دیگه بلکل قدیمی شدن هیچکس دیگه نیگاهم بهشون نمیندازه این تایپیکم زدم تا به مباحث چندجمله ای و نامساوی بپردازیم و اندکی مواقع تابع برای امادگی م2 .
قوانین همون قوانین ماراتنای قبلی هرکس سوالی حل کرد سوال جدید میذاره .
1
ایا چندجمله ای غیر ثابت

$p(x)$

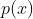با ضرایب صحیح وجود دارد که

$p(1),p(2),p(3),...$

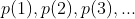همگی اعدادی اول باشند .

darya.f · 1393/6/15

پاسخ : ماراتن جبر

math1998 گفت

$P(m)=q ,m-n=q\rightarrow m|p(m)-p(n)\rightarrow q|p(n)\rightarrow p(n)=q=p(m)$

q عددى اول هست ...بنابر اىن چندجمله اى ثابت مىشه که تناقضه

---- دو نوشته به هم متصل شده است ----

math1998 گفت

$P(m)=q ,m-n=q\rightarrow m|p(m)-p(n)\rightarrow q|p(n)\rightarrow p(n)=q=p(m)$

q عددى اول هست ...بنابر اىن چندجمله اى ثابت مىشه که تناقضه

---- دو نوشته به هم متصل شده است ----

اگه مىشه خودتون سوال بزارىد من فعلا سوال خوب ندارم

math1998 · 1393/6/15

پاسخ : ماراتن جبر

darya.f گفت

به این سادگی ها هم نیست

$n$

ای که شما انتخاب کردی عددی خاصه و برای همه اعداد صحیح صادق نیست دقیق تر باشید.

darya.f · 1393/6/15

پاسخ : ماراتن جبر

math1998 گفت

ببخشىد مگه نباىد p ها متماىز باشن خب من الان ىه m,n اى پىدا کردم که p شون ىکى شد خب اىن تناقضه دىگه کارى به بقىه m,n ها نداره که!

Dadgarnia · 1393/6/15

پاسخ : ماراتن جبر

math1998 گفت

فرض كنيد

$p(m)=p$

كه p يه عدد اوله و فرض كنيد

$p(x)=\sum_{i=0}^{n}a_ix^i$

و داريم:

$p(m+kp)=\sum_{i=0}^{n}a_im^i+tp=(t+1)p$

به ازاي هر kي طبيعي. پس k اي موجود است كه (p(m+kp عددي اول نيست.

math1998 · 1393/6/15

پاسخ : ماراتن جبر

darya.f گفت

لزوما اینطور نیست چندجمله ای هم یه نوع تابعست اگر تابع به ازای 2 مقدار ثابت باشه یعنی در کل ثابته ؟؟!!!

darya.f · 1393/6/15

پاسخ : ماراتن جبر

math1998 گفت

نه کارى به ثابت بودن ىا نبودن ندارم ..بله در اون مورد شما درست مىگىد من منظورم اىنه که من 2تا m,n پىدا کردم که pشون ىکى شده در حالىکه براى هىچ m,nاى نباىد اىن جورى باشه نگفتم که چون واسه 2تا ىکى شده بره همه اىن جورىه!!

math1998 · 1393/6/15

پاسخ : ماراتن جبر

darya.f گفت

چرا نباید برا هیچ 2 تایی اینطور بشه ؟!

AHZolfaghari · 1393/6/15

پاسخ : ماراتن جبر

فکر کنم منظور خانوم darya.f این بوده باشه ! :

$P(m)=q$

$m-n \vert P(m)-P(n)$

$n\rightarrow m+q\Rightarrow q \vert P(n)\Rightarrow p(n+q)=q$

به همین ترتیب به ازای هر k طبیعی

$P(m+kq)=q$

برقرار است پس چند جمله ای

$P(x)-q$

بی نهایت ریشه دارد که تناقضه پس باید ثابت باشه

پس

$P(x)=q$

که q یه عدد اول هستش صدق میکنه

2
تمامی توابع f از اعداد گویای مثبت به خودش را بیابید بطوریکه :

$f(x+1)=f(x)+1 , f(x)^2=f(x^2)$

همون قدر که چند جمله ای احتمال داره همون قدر نامساوی احتمال داره بیاد و همون قدر تابع احتمال داره بیاد پس چه خوبه رو هر سه قسمت کار بشه

ترجیحا هم از سوالات سبک شروع بشه و سطحش رفته رفته بالاتر بره

darya.f · 1393/6/15

پاسخ : ماراتن جبر

math1998 گفت

چون قراره هر دو تاىى pشون متفاوت باشه

AhmadrezaBM · 1393/6/16

پاسخ : ماراتن جبر

ببخشید من سوال حل نکردم ولی یک سوال داشتم:
اگر a و b دو دنباله بصورت:

$a_{1} , a_{2} , a_{n}=a_{n-1}+a_{n-2}$

$b_{1} , b_{2} , b_{n}=b_{n-1}+b_{n-2}$

حاصل عبارت زیر را چطور میتوان بدست آورد؟

$\lim_{i\rightarrow \infty }\frac{b_{i}}{a_{i}}$

Dadgarnia · 1393/6/16

پاسخ : ماراتن جبر

AHZolfaghari گفت

به راحتي مي توانيم بدست بياوريم:

$f(x+n)=f(x)+n \forall n \in \mathbb{N}$

با توجه به اين رابطه داريم:

$f((\frac{p}{q}+q)^2)=f(\frac{p}{q})^2+2p++q^2=f(\frac{p}{q})^2+2qf(\frac{p}{q})+q^2\Rightarrow f(\frac{p}{q})=\frac{p}{q}$

math1998 · 1393/6/16

پاسخ : ماراتن جبر

تمام توابع

$f:\mathbb{R}\rightarrow \mathbb{R}$

را بیابید .

$f(x+y)=f(y).f(x).f(xy)$

در ضمن منظور من این نبوذ که تابع کار نکنیم ولی گفتم که بیشتر اون دوتای دیگه رو کار کنید اگر هم سوال تابع میذارید سوالی ایده دار بذارید!!!

Dadgarnia · 1393/6/16

پاسخ : ماراتن جبر

math1998 گفت

فرض كنيد رابطه ي بالا

$P(x,y)$

باشد پس داريم:
(1)

$P(x,1)\rightarrow f(x+1)=f(x)^2f(1)$

با استفاده از رابطه ي بالا داريم:

$P(x,y+1)\rightarrow f(x+y)^2=f(x)f(y)^2f(xy+x)$

با استفاده از رابطه ي بالا و رابطه ي اصلي مسئله داريم:

$f(xy)f(x+y)=f(y)f(xy+x)$

با قرار دادن y=1 در رابطه ي بالا و استفاده از رابطه ي (1) داريم:

$f(2x)=f(x)^3$

با استفاده از رابطه ي بالا داريم:

$P(x,x)\rightarrow f(x)=f(x^2)$

با قرار دادن x- در رابطه ي بالا داريم:

$f(x^2)=f(x)=f(-x)$

با استفاده از رابطه ي بالا داريم:

$P(x,-x)\rightarrow f(x)^3=f(0)$

و (f(0 مي تونه صفر يا 1 يا 1- باشه كه نتيجه ميده سه تابع

$f(x)\equiv 0$

و

$f(x)\equiv 1$

و

$f(x)\equiv -1$

در شرايط مسئله صدق مي كنند.

math1998 · 1393/6/16

پاسخ : ماراتن جبر

Dadgarnia گفت

فرض كنيد رابطه ي بالا

$P(x,y)$

باشد پس داريم:
(1)

$P(x,1)\rightarrow f(x+1)=f(x)^2f(1)$

با استفاده از رابطه ي بالا داريم:

$P(x,y+1)\rightarrow f(x+y)^2=f(x)f(y)^2f(xy+x)$

با استفاده از رابطه ي بالا و رابطه ي اصلي مسئله داريم:

$f(xy)f(x+y)=f(y)f(xy+x)$

با قرار دادن y=1 در رابطه ي بالا و استفاده از رابطه ي (1) داريم:

$f(2x)=f(x)^3$

با استفاده از رابطه ي بالا داريم:

$P(x,x)\rightarrow f(x)=f(x^2)$

با قرار دادن x- در رابطه ي بالا داريم:

$f(x^2)=f(x)=f(-x)$

با استفاده از رابطه ي بالا داريم:

$P(x,-x)\rightarrow f(x)^3=f(0)$

و (f(0 مي تونه صفر يا 1 يا 1- باشه كه نتيجه ميده سه تابع

$f(x)\equiv 0$

و

$f(x)\equiv 1$

و

$f(x)\equiv -1$

در شرايط مسئله صدق مي كنند.

درسته فقط من یه ایده دیگه مد نظر دارم که که بعضی سوالا رو خیلی قشنگ حل میکنه اگر کسی چیز دیگه ای نگفت میگم .

Dadgarnia · 1393/6/16

پاسخ : ماراتن جبر

math1998 گفت

يه راه ديگه به ذهنم رسيد:

$P(x+y,z)\rightarrow f(x+y+z)=f(x+y)f(z)f(xz+yz)=f(x)f(y)f(z)f(xy)f(yz)f(zx)f(xyz^2)$

پس داريم:

$f(x^2yz)=f(xy^2z)$

حالا در رابطه ي بالا

$z=\frac{1}{x^4}$

و

$y=x^2$

كه نتيجه مي دهد:

$f(x)=f(1)$

بقيه راه حل هم مشابه قبل است.

math1998 · 1393/6/16

پاسخ : ماراتن جبر

Dadgarnia گفت

عالیه دقیقا همینه یه ایده ی باحال برا حل سوالات تابعیه اینم ایده ی مشابه البته این یکی خیلی ساده تره

$f(\frac{x+y}{2})=\sqrt{f(x).f(y)}$

Dadgarnia · 1393/6/16

پاسخ : ماراتن جبر

math1998 گفت

فكر مي كنم يكي از شرايط اين سوال پيوسته بودن f باشه. اگه اينجوري باشه فرض كنيد رابطه ي بالا

$P(x,y)$

باشه. داريم:

$P(x+y,0)\rightarrow f(x+y)f(0)=f(x)f(y)$

يكي از جواب ها

$f(x)\equiv 0$

است در غير اين صورت تعريف مي كنيم

$g(x)=\frac{f(x)}{f(0)}$

كه نتيجه مي دهد:

$g(x+y)=g(x)g(y)$

كه از توابع كوشي است. پس تابع ديگر

$f(x)=Ck^x$

است كه C,k بزرگتر از صفرند.

Dadgarnia · 1393/6/17

پاسخ : ماراتن جبر

5
تمام توابع

$f:\mathbb{R}^+\cup \left \{ 0 \right \} \mapsto \mathbb{R}^+\cup \left \{ 0 \right \}$

و صعودي را بيابيد به طوري كه براي هر

$x,y\in \mathbb{R}^+\cup \left \{ 0 \right \}$

داشته باشيم:

$f(\frac{x+f(x)}{2}+y)=2x-f(x)+f(f(y))$

math1998 · 1393/6/17

پاسخ : ماراتن جبر

Dadgarnia گفت

سوال iran TST 2010 بوده فقط باید با توجه به اینکه پوشاست و مقدارگذاری مناسب میتونیم(راه حلش طولانیه) بذست بیاریم

$f(0)=0$

و بعد میتونید نتیجه بگیرید

$f(x)=x$

قسمت سختش فقط بدست اوردن

$f(0)$

یادمه یه جایی برااین سوال 7-8 تا راه حل دیدم.:3:

ماراتن جبر

New Member

New Member

New Member

New Member

New Member

New Member

New Member

New Member

Well-Known Member

New Member

New Member

New Member

New Member

New Member

New Member

New Member

New Member

New Member

New Member

New Member