ماراتن نظریه ی اعداد (سطح ممتاز)
پاسخ : ماراتن نظریه ی اعداد (سطح ممتاز)
باشه ، اینم راه حلّش . سوال بعد رو خودتون بذارید
AoPS Forum - Functional Equations Marathon • Art of Problem Solving
باشه ، اینم راه حلّش . سوال بعد رو خودتون بذارید
26
Find all .......
)&space;=&space;f(n+1)f(n-1)&space;-&space;f(n)^2&space;\;&space;\;&space;\;&space;(n&space;\geq&space;2))
Find all .......
پاسخ : ماراتن نظریه ی اعداد (سطح ممتاز)
فقط راه حلش یک صفحه عقب تره !!! AoPS Forum - Functional Equations Marathon • Art of Problem Solving
سوال بعد :
اگر داشته باشیم
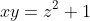
ثابت کنید اعداد
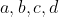 ای موجودند که
ای موجودند که

فقط راه حلش یک صفحه عقب تره !!! AoPS Forum - Functional Equations Marathon • Art of Problem Solving
سوال بعد :
اگر داشته باشیم
ثابت کنید اعداد
پاسخ : ماراتن نظریه ی اعداد (سطح ممتاز)
هم به خاطر بالا اومدن تاپیک هم یک راهنمایی : اگر داشته باشیم
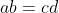 انگاه اعداد
انگاه اعداد
 موجود اند به طوری که
موجود اند به طوری که

فقط راه حلش یک صفحه عقب تره !!! AoPS Forum - Functional Equations Marathon • Art of Problem Solving
سوال بعد :
اگر داشته باشیم
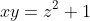
ثابت کنید اعداد
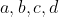 ای موجودند که
ای موجودند که

سوال بعد :
اگر داشته باشیم
ثابت کنید اعداد
هم به خاطر بالا اومدن تاپیک هم یک راهنمایی : اگر داشته باشیم
پاسخ : ماراتن نظریه ی اعداد (سطح ممتاز)
دقت کردید استاد ماهان یک سوال میذارن بعد راهنمایی میکنن و بعد جوابش رو میدن و بعد یکی دیگه میاد سوال میذاره خودش راهنمایی میکنه و جوابش رو خودش میده !!! خوب الان سوالش سخته کسی جواب نمیده ؟؟؟ یا مشکل دیگه ای هستش ؟؟
راهمایی 2 : میتوانید از
 استفاده کنید !!
استفاده کنید !!
حال ثابت کنید
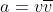 و....
و....
دقت کردید استاد ماهان یک سوال میذارن بعد راهنمایی میکنن و بعد جوابش رو میدن و بعد یکی دیگه میاد سوال میذاره خودش راهنمایی میکنه و جوابش رو خودش میده !!! خوب الان سوالش سخته کسی جواب نمیده ؟؟؟ یا مشکل دیگه ای هستش ؟؟
راهمایی 2 : میتوانید از
حال ثابت کنید
- ارسال ها
- 115
- لایک ها
- 18
- امتیاز
- 0
پاسخ : ماراتن نظریه ی اعداد (سطح ممتاز)
برای سوال 25 یه راه قشنگ من دارم(!!):
دنباله ی f i را همون دنباله فیبوناتچی می گیریم با این تفاوت که اولین و دمین عضو اون i هستند و عضو هاش رو به پیمانه p نوشتیم
g(i) رو هم برار با کو چکترین اندیس در دنباله fi می گیریم که a i = a i+1 باشد
حال با توجه به اول بودن p می توان ثابت کرد تمام gi ها با هم برابر هستند (i<=p-1)
حالا می توان ثابت کرد هر زوج مرتب از اعداد به پیمانه p فقط در یکی از fi ها آمده
حالا چون به پیمانه p تعداد جفت پیمانه p حداکثر 1- p^2 است (0و0 نداریم) پس می توان نتیجه گرفت دوره تناوب fi ها حداکثر برابر با p+1 است که است و چون عضو قبل از 2 عضو برابر در دنباله اصلی به پیمانه p برابر با 0 است و ابتدای دنباله اصلی همان اعضای f1 هستند پس حکم را می توان نتیجه گرفت...
برای سوال 25 یه راه قشنگ من دارم(!!):
دنباله ی f i را همون دنباله فیبوناتچی می گیریم با این تفاوت که اولین و دمین عضو اون i هستند و عضو هاش رو به پیمانه p نوشتیم
g(i) رو هم برار با کو چکترین اندیس در دنباله fi می گیریم که a i = a i+1 باشد
حال با توجه به اول بودن p می توان ثابت کرد تمام gi ها با هم برابر هستند (i<=p-1)
حالا می توان ثابت کرد هر زوج مرتب از اعداد به پیمانه p فقط در یکی از fi ها آمده
حالا چون به پیمانه p تعداد جفت پیمانه p حداکثر 1- p^2 است (0و0 نداریم) پس می توان نتیجه گرفت دوره تناوب fi ها حداکثر برابر با p+1 است که است و چون عضو قبل از 2 عضو برابر در دنباله اصلی به پیمانه p برابر با 0 است و ابتدای دنباله اصلی همان اعضای f1 هستند پس حکم را می توان نتیجه گرفت...
پاسخ : ماراتن نظریه ی اعداد (سطح ممتاز)
به جا هایی رسیدم ولی الان وقتشو ندارم ادامه بدم:
در هر مرحله بزرگترین عامل اول کوچک تر میشه به جز حالتی که بزرگترین عامل 2یا3 هستش.پس از یه جایی به بعد عدد موردنظر یا توانی از 2 هستش یا 3 و یا عدد برابر 1 هستش.اگه در مرحله توان 2 بزرگتر از 4 باشه اون وقت دنباله بیکران هستش مثلا تمامی اعداد مضرب 32 تشکیل دنباله بی کران رو میدن.البته این کل اعداد نیست جالا ....:4:
یا اعدادی که بر 16 بخشپذیر باشند و یه عامل 3k-1 با توانی بزرگتر از 1 داشته باشن هم تشکیل دنباله نامتناهی رو میدن.........
به جا هایی رسیدم ولی الان وقتشو ندارم ادامه بدم:
در هر مرحله بزرگترین عامل اول کوچک تر میشه به جز حالتی که بزرگترین عامل 2یا3 هستش.پس از یه جایی به بعد عدد موردنظر یا توانی از 2 هستش یا 3 و یا عدد برابر 1 هستش.اگه در مرحله توان 2 بزرگتر از 4 باشه اون وقت دنباله بیکران هستش مثلا تمامی اعداد مضرب 32 تشکیل دنباله بی کران رو میدن.البته این کل اعداد نیست جالا ....:4:
یا اعدادی که بر 16 بخشپذیر باشند و یه عامل 3k-1 با توانی بزرگتر از 1 داشته باشن هم تشکیل دنباله نامتناهی رو میدن.........
پاسخ : ماراتن نظریه ی اعداد (سطح ممتاز)
بله ایده حل سوال همینه
دیدم از مراتن نامساوی استقبال شد گفتم شاید از این هم استقبال بشه
سوال بعد :


برای هر n ثابت کنید
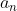 مربع کامل است
مربع کامل است
به جا هایی رسیدم ولی الان وقتشو ندارم ادامه بدم:
در هر مرحله بزرگترین عامل اول کوچک تر میشه به جز حالتی که بزرگترین عامل 2یا3 هستش.پس از یه جایی به بعد عدد موردنظر یا توانی از 2 هستش یا 3 و یا عدد برابر 1 هستش.اگه در مرحله توان 2 بزرگتر از 4 باشه اون وقت دنباله بیکران هستش مثلا تمامی اعداد مضرب 32 تشکیل دنباله بی کران رو میدن.البته این کل اعداد نیست جالا ....:4:
یا اعدادی که بر 16 بخشپذیر باشند و یه عامل 3k-1 با توانی بزرگتر از 1 داشته باشن هم تشکیل دنباله نامتناهی رو میدن.........
در هر مرحله بزرگترین عامل اول کوچک تر میشه به جز حالتی که بزرگترین عامل 2یا3 هستش.پس از یه جایی به بعد عدد موردنظر یا توانی از 2 هستش یا 3 و یا عدد برابر 1 هستش.اگه در مرحله توان 2 بزرگتر از 4 باشه اون وقت دنباله بیکران هستش مثلا تمامی اعداد مضرب 32 تشکیل دنباله بی کران رو میدن.البته این کل اعداد نیست جالا ....:4:
یا اعدادی که بر 16 بخشپذیر باشند و یه عامل 3k-1 با توانی بزرگتر از 1 داشته باشن هم تشکیل دنباله نامتناهی رو میدن.........
دیدم از مراتن نامساوی استقبال شد گفتم شاید از این هم استقبال بشه
سوال بعد :
پاسخ : ماراتن نظریه ی اعداد (سطح ممتاز)
ایده ی این سوالا عموما اینطوریه که حدس می زنیم. الانم من فقط با دیدن جملات و حدس زدن اینا رو بدست آوردم:
تعریف کنید
 و ثابت کنید
و ثابت کنید
^{2})
گرچه خلاف قوانین ماراتنه ولی چون من کم ایجا سر میزنم و بچه ها خیلی از سوت و کور بون اینجا مینالند بیش از یه سوال میذارم. ببخشید!
ایده ی سوالا تقریبا شبیه همه . امیدوارم به دردتون بخوره
1. برای هر n طبیعی ثابت کنید :

2. aوbوc صحیحند و
 صحیح شده. ثابت کنید abc مکعب کامله.
صحیح شده. ثابت کنید abc مکعب کامله.
3. a عددی طبیعیه و n طبیعی و بزرگتر از یکه و برای هر k طبیعی عدد طبیعی
 موجوده که
موجوده که
^{n}) . ثابت کنید a توان nام کامله.
. ثابت کنید a توان nام کامله.
بله ایده حل سوال همینه
دیدم از مراتن نامساوی استقبال شد گفتم شاید از این هم استقبال بشه
سوال بعد :


برای هر n ثابت کنید
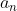 مربع کامل است
مربع کامل است
دیدم از مراتن نامساوی استقبال شد گفتم شاید از این هم استقبال بشه
سوال بعد :
تعریف کنید
گرچه خلاف قوانین ماراتنه ولی چون من کم ایجا سر میزنم و بچه ها خیلی از سوت و کور بون اینجا مینالند بیش از یه سوال میذارم. ببخشید!
ایده ی سوالا تقریبا شبیه همه . امیدوارم به دردتون بخوره
1. برای هر n طبیعی ثابت کنید :
2. aوbوc صحیحند و
3. a عددی طبیعیه و n طبیعی و بزرگتر از یکه و برای هر k طبیعی عدد طبیعی
