ماراتن نظریه ی اعداد (سطح ممتاز)
پاسخ : ماراتن نظریه ی اعداد (سطح ممتاز)
سلام. نمیدونم چرا چند وقته یک مشکلی توی آیریسک دارم که هر چی اینتر میزنم نمیره خط بعد. مجبورم پشت سر هم بنویسم. ببخشید. n عددی طبیعی است. الف) ثابت کنید
 ب) ثابت کنید
ب) ثابت کنید
 عامل اولی بزرگتر از
عامل اولی بزرگتر از
 دارد. ( قسمت الف و ب از یک سوال نیستند. بلکه قسمت الف رو گفتم که تو راه حلش یک نکته ای یادآوری بشه که تو حل ب بدرد میخوره)
دارد. ( قسمت الف و ب از یک سوال نیستند. بلکه قسمت الف رو گفتم که تو راه حلش یک نکته ای یادآوری بشه که تو حل ب بدرد میخوره)
سلام. نمیدونم چرا چند وقته یک مشکلی توی آیریسک دارم که هر چی اینتر میزنم نمیره خط بعد. مجبورم پشت سر هم بنویسم. ببخشید. n عددی طبیعی است. الف) ثابت کنید
پاسخ : ماراتن نظریه ی اعداد (سطح ممتاز)
خب بقیش اصلا ساده نیست.بقیش رو لطف کنید بنویسید.شما فقط قسمت بدیهی سوال رو گفتید.
خب من این سوال رو حل کردم . اگه خواستید جوابش رو مینویسم.
ولی توجه کنید که تو دوره امسال هیچکس این سوال رو حل نکرده.
پس بقیش به این راحتی نیست.
ابتدا لمی رو بیان میکنیم :
تمام عوامل اول
 به شکل
به شکل
 هستند .
هستند .
حال با این لم قسمت الف بدیهیه و قسمت ب رو هم به این نکته توجه کنید که
 اگراول باشد مساله حل است و اگر نباشد یه عامل اول کوچک تر از ....... داره !!!!
اگراول باشد مساله حل است و اگر نباشد یه عامل اول کوچک تر از ....... داره !!!!
اثبات لم هم با مرتیبه به راحتی قابل اثباته :3:
تمام عوامل اول
حال با این لم قسمت الف بدیهیه و قسمت ب رو هم به این نکته توجه کنید که
اثبات لم هم با مرتیبه به راحتی قابل اثباته :3:
خب بقیش اصلا ساده نیست.بقیش رو لطف کنید بنویسید.شما فقط قسمت بدیهی سوال رو گفتید.
خب من این سوال رو حل کردم . اگه خواستید جوابش رو مینویسم.
ولی توجه کنید که تو دوره امسال هیچکس این سوال رو حل نکرده.
پس بقیش به این راحتی نیست.
پاسخ : ماراتن نظریه ی اعداد (سطح ممتاز)
:4::4:
من گفتم بقیش سادس ایا ؟؟ :4:
هدف ماراتن قوی تر شدن حل کننده هر مساله نیست قوی تر شدن همس پس بهتره برای هر سوال اول راهنمایی گذاشته بشه و بعد حل ( البته به استثنای سوالاتی که مدت زیادی حل نشده اند )
خب بقیش اصلا ساده نیست.بقیش رو لطف کنید بنویسید.شما فقط قسمت بدیهی سوال رو گفتید.
خب من این سوال رو حل کردم . اگه خواستید جوابش رو مینویسم.
ولی توجه کنید که تو دوره امسال هیچکس این سوال رو حل نکرده.
پس بقیش به این راحتی نیست.
خب من این سوال رو حل کردم . اگه خواستید جوابش رو مینویسم.
ولی توجه کنید که تو دوره امسال هیچکس این سوال رو حل نکرده.
پس بقیش به این راحتی نیست.
:4::4:
من گفتم بقیش سادس ایا ؟؟ :4:
هدف ماراتن قوی تر شدن حل کننده هر مساله نیست قوی تر شدن همس پس بهتره برای هر سوال اول راهنمایی گذاشته بشه و بعد حل ( البته به استثنای سوالاتی که مدت زیادی حل نشده اند )
پاسخ : ماراتن نظریه ی اعداد (سطح ممتاز)
خب از حرف هایی که میزنید معلوم میشه حل شما اون قدر سخت نیست.
ولی این سوال رو آقای جمالی سر کلاس دادن اگر چه سه تا راه حل از بچه های مدرسمون داده شد ولی باز هم از نظر آقای جمالی سوال سختیه.
آقای جمالی گفت که این سوال رو کسی تو دوره حل نکرده.
خب از حرف هایی که میزنید معلوم میشه حل شما اون قدر سخت نیست.
ولی این سوال رو آقای جمالی سر کلاس دادن اگر چه سه تا راه حل از بچه های مدرسمون داده شد ولی باز هم از نظر آقای جمالی سوال سختیه.
آقای جمالی گفت که این سوال رو کسی تو دوره حل نکرده.
آخرین ویرایش توسط مدیر
پاسخ : ماراتن نظریه ی اعداد (سطح ممتاز)
در موزد اینکه این سوال رو کسی تو دوره حل نکرده و ابنا چیزی نمی دونم. در ضمن خیلی وقت ها بعضی بچه ها تو دوره سوالی رو حل میکنن و نمیگن حل کردن. اما بدون تردید این سوال سوال سختیه و بقیه ی حلش اصلا بدیهی نیست. این سوال سوال 3 از quiz6 انتخاب تیم چین2005 بوده و همین یعنی سوال اصلا ساده نیست. اگر کسی تا یکی دو روز آینده به جایی نرسید آقای math لطفا حل کاملش رو بگذاره. بعدش میتونیم بریم سراغ سوال بعدی. موفق باشید
در موزد اینکه این سوال رو کسی تو دوره حل نکرده و ابنا چیزی نمی دونم. در ضمن خیلی وقت ها بعضی بچه ها تو دوره سوالی رو حل میکنن و نمیگن حل کردن. اما بدون تردید این سوال سوال سختیه و بقیه ی حلش اصلا بدیهی نیست. این سوال سوال 3 از quiz6 انتخاب تیم چین2005 بوده و همین یعنی سوال اصلا ساده نیست. اگر کسی تا یکی دو روز آینده به جایی نرسید آقای math لطفا حل کاملش رو بگذاره. بعدش میتونیم بریم سراغ سوال بعدی. موفق باشید
پاسخ : ماراتن نظریه ی اعداد (سطح ممتاز)
سلام
من متاسفانه تا دو روز دیگه نیستم برای همین یه راهنمایی کوچیک دیگه میزارم که واقعا از این به بعد اثبات ساده است ( بدیهی نیست )
)
ابتدا لم بیان شده را یکم !!! قوی تر میکنیم
ثابت کنید اگر داشته باشیم :

اثبات لم :
میدانیم که اگز n بزرگتر از 3 باشد انگاه داریم
 چون
چون
 ( چرا ؟؟)
( چرا ؟؟) . حال پس میدانیم
. حال پس میدانیم
 حال به وضوح داریم
حال به وضوح داریم
 پس حکم مساله نتیجه شد !!!!
پس حکم مساله نتیجه شد !!!!
حال به این نکته توجه کنید که :

سلام
من متاسفانه تا دو روز دیگه نیستم برای همین یه راهنمایی کوچیک دیگه میزارم که واقعا از این به بعد اثبات ساده است ( بدیهی نیست
ابتدا لم بیان شده را یکم !!! قوی تر میکنیم
ثابت کنید اگر داشته باشیم :
میدانیم که اگز n بزرگتر از 3 باشد انگاه داریم
حال به این نکته توجه کنید که :
آخرین ویرایش توسط مدیر
پاسخ : ماراتن نظریه ی اعداد (سطح ممتاز)
آقا میتونید حل این سوال رو بگید
درسته. یه نکته ی جانبی: در مورد دنباله ی فیبوناچی هم قضیه ی مشابهی برقراره: برای هر
 ،
،
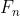 عامل اولی داره که توی جملات قبل نیومده. سوال بعد:
عامل اولی داره که توی جملات قبل نیومده. سوال بعد:
[center:05b73bfa0e]

[center:05b73bfa0e]
ثابت کنید عددی وجود ندارد که در دنباله ی
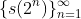 بی نهایت بار تکرار شود. (
بی نهایت بار تکرار شود. (
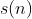 مجموع ارقام عدد طبیعی
مجموع ارقام عدد طبیعی
 است.)
است.)
[/center:05b73bfa0e]
