ماراتن هندسه
خوب دیگه .چون هدف ما دیدن یه عالمه سوال تو این روزای آخره ، فک کنم 2 روز واسه هر سوال کافیه دیگه .....
و اما جواب:
وسطAQ را L بنامید.وسط LQراM هم بنامید.از KبهQ وL وصل کنید. بنا به حالت ض ز ض دو مثلثALK و QKCهم نهشتند.
CKM=60
(SIN CKQ/SIN QKM)*(KC/KM)=(CQ/QM) PAS CKQ=QKM=30
پس مثلثLKQ متساوی الاضلاعه. پس چهارضلعی ALKB محاطیه . پس LBK=30
وسط KC را R بنامید و ازQ بهR وصل کنید.چهار ضلعی MQRKمحاطیه .چون QMR=QKR=30پس QRK=90
PR موازی با KB هست . PQ هم موازی با LB هست. از این دو نکته بدست میادکه QPR=30 هست.پس QKRP هم محاطیه . پس KPQ=90 . پس حکم هماثبات شد. امیدوارم اشکال تایپی نداشته باشم.
" لطفا یکی سوال بعدی رو بذاره "
و اما جواب:
وسطAQ را L بنامید.وسط LQراM هم بنامید.از KبهQ وL وصل کنید. بنا به حالت ض ز ض دو مثلثALK و QKCهم نهشتند.
CKM=60
(SIN CKQ/SIN QKM)*(KC/KM)=(CQ/QM) PAS CKQ=QKM=30
پس مثلثLKQ متساوی الاضلاعه. پس چهارضلعی ALKB محاطیه . پس LBK=30
وسط KC را R بنامید و ازQ بهR وصل کنید.چهار ضلعی MQRKمحاطیه .چون QMR=QKR=30پس QRK=90
PR موازی با KB هست . PQ هم موازی با LB هست. از این دو نکته بدست میادکه QPR=30 هست.پس QKRP هم محاطیه . پس KPQ=90 . پس حکم هماثبات شد. امیدوارم اشکال تایپی نداشته باشم.
" لطفا یکی سوال بعدی رو بذاره "
- ارسال ها
- 335
- لایک ها
- 8
- امتیاز
- 0
zek واقعا دستت درد نکنه سوال جالبی بود!

این هم سوال بعد :
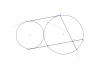
دو دایره بر هم مماس خارجند. و AD مماس مشترک خارجی آن ها است. یک مماس بردایره ی کوچکتر موازی AD رسم میکنیم
تا دایره ی دیگر را در P , Q قطع کند.وتری دلخواه که از D از دایره ی بزرگتر رسم میشود PQ را در B و دایره رادر C قطع میکند.
ثابت کنید دایره ی محیطی ABC بر AD مماس است.

این هم سوال بعد :
دو دایره بر هم مماس خارجند. و AD مماس مشترک خارجی آن ها است. یک مماس بردایره ی کوچکتر موازی AD رسم میکنیم
تا دایره ی دیگر را در P , Q قطع کند.وتری دلخواه که از D از دایره ی بزرگتر رسم میشود PQ را در B و دایره رادر C قطع میکند.
ثابت کنید دایره ی محیطی ABC بر AD مماس است.
پیوست ها
-
22.5 کیلوبایت بازدیدها 66
- ارسال ها
- 335
- لایک ها
- 8
- امتیاز
- 0
آقایون این قضیه ی شکل کشیدن رو صد بار پرسیدند و جواب دادیم.(این قضیه ی های شخصی رو با پیغام شخصی بپرسید)
ابتدا تو یه نرم افزار شکل رو میکشید.بعد دکمه ی PRINT SCREEN را در کیبورد فشار میدید و سپس در paint راست کلیک کرده و paste را میزنید و کل صفحه میاید و سپس شما قسمت مورد نظر را
جدا میکنید و راست کلیک کرده و copy را میزنید و در یک صفحه ی جدید paint راست کلیک کرده و گزینه ی paste را میزنید و سپس فایل را با پسوند .png ذخیره میکنید و در قسمت ارسال جواب این
فایل را وارد فایل ضمیمه میکنید و تمام.
اگر نامفهوم است از طریق pm سوال فرمایید با تشکر فراوان.
آقایون و خانمها سوال رو حل کنید اصلا سخت نیست مثل قیافش آسونه.
ابتدا تو یه نرم افزار شکل رو میکشید.بعد دکمه ی PRINT SCREEN را در کیبورد فشار میدید و سپس در paint راست کلیک کرده و paste را میزنید و کل صفحه میاید و سپس شما قسمت مورد نظر را
جدا میکنید و راست کلیک کرده و copy را میزنید و در یک صفحه ی جدید paint راست کلیک کرده و گزینه ی paste را میزنید و سپس فایل را با پسوند .png ذخیره میکنید و در قسمت ارسال جواب این
فایل را وارد فایل ضمیمه میکنید و تمام.
اگر نامفهوم است از طریق pm سوال فرمایید با تشکر فراوان.
آقایون و خانمها سوال رو حل کنید اصلا سخت نیست مثل قیافش آسونه.
[font=Arial,sans-serif]برای اثبات حکم رابطه ی زیر باید درست باشد(فرض می کنیم شعاع دایره های بزرگ و کوچک به ترتیب [/font]R
[font=Arial,sans-serif]
و[/font]r
[font=Arial,sans-serif]
باشد.)<?xml:namespace prefix = o ns = "urn:schemas-microsoft-com ffice
ffice ffice" /><o
ffice" /><o ></o
></o >[/font]
>[/font]
AD[SUP]2 [/SUP]=DB.DC [font=Calibri,sans-serif]<?xml:namespace prefix = v ns = "urn:schemas-microsoft-com:vml" /><v:shapetype id=_x0000_t75 stroked="f" filled="f" path="m@4@5l@4@11@9@11@9@5xe" o[font=Arial,sans-serif]
و[/font]r
[font=Arial,sans-serif]
باشد.)<?xml:namespace prefix = o ns = "urn:schemas-microsoft-com
[center:b054f2ad8d]d
[font=Arial,sans-serif]
از مرکز دایره ی بزرگ برابر [/font]B [font=Arial,sans-serif]نسبت به دایره ی بزرگ است.(فرض کنید فاصله ی [/font]
B [font=Arial,sans-serif]همان قوت نقطه ی [/font]
DB.DC[font=Arial,sans-serif]<o
[font=Arial,sans-serif]باشد.)<o ></o
></o >[/font]
>[/font]
R[SUP]2 [/SUP]–d[SUP]2 [/SUP]=PB.BQ=DP[SUP]2 [/SUP]–DB[SUP]2 [/SUP] [font=Calibri,sans-serif]<v:shape style="WIDTH: 9.75pt; HEIGHT: 21pt" id=_x0000_i1025 type="#_x0000_t75"> <v:imagedata chromakey="white" o:title="" src="file:///C:\Users\aa\AppData\Local\Temp\msohtmlclip1\01\clip_image001.png"></v:imagedata></v:shape>[/font]AD[SUP]2 [/SUP]=DB[SUP]2 [/SUP]+DP[SUP]2 [/SUP]–DB[SUP]2 [/SUP]=DP[SUP]2 <o[font=Arial,sans-serif]پس باید ثابت کنیم :[/font]AD=DP<o ></o
></o >
>
AD[SUP]2 [/SUP]=(r+R)[SUP]2 [/SUP]–(R-r)[SUP]2 [/SUP]=4Rr<o ></o
></o >
>
DP[SUP]2 [/SUP]=(PQ/2)[SUP]2 [/SUP]+4r[SUP]2 [/SUP]<o ></o
></o >
>
(PQ/2)[SUP]2 [/SUP]+(2r-R)[SUP]2 [/SUP]=R[SUP]2 [/SUP] [SUP] <o ></o
></o >[/SUP]
>[/SUP]
DP[SUP]2 [/SUP]=4Rr[SUP]<o ></o
></o >[/SUP]
>[/SUP]
AD[SUP]2[/SUP]=DP[SUP]2[/SUP]=4Rr<o[font=Calibri,sans-serif]<v:shape style="WIDTH: 19.5pt; HEIGHT: 16.5pt" id=_x0000_i1025 type="#_x0000_t75"> <v:imagedata chromakey="white" o:title="" src="file:///C:\Users\aa\AppData\Local\Temp\msohtmlclip1\01\clip_image003.png"></v:imagedata></v:shape>[/font]
<o
[font=Arial,sans-serif]پس حکم مسئله ثابت شد [/font]<o ></o
></o >
>
- ارسال ها
- 335
- لایک ها
- 8
- امتیاز
- 0
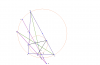
D را محل برخورد ST و RQ بگیرید.
اگر RQ دایره را در M و N قطع کند داریم : M وسط کمان AC و N وسط کمان AB است(چرا؟)
اگر P محل تماس دایره ی محاطی با BC باشد داریم : BM و PQ و ST در K همرسند و PR و CN و ST در L همرسند.
داریم : KL موازی BC است پس :CPQ=LKP=PRQ (زاویه) پس RQKL محاطی است پس DK×KL=DQ×DR .
TMNS محاطی است پس : DT×DS=DM×DN و از طرفی داریم : CLK=BCI=BMN (زاویه) پس NLKM محاطی است پس : DM×DN=DK×DL .
حال از این سه رابطه ( DK×KL=DQ×DR و DT×DS=DM×DN و DM×DN=DK×DL ) نتیجه میگیریم : DQ×DR=DT×DS پس : SRQT محاطی است.
سوال خیلی باحالی بود حدود 5 ساعت روش فکر کردم و خدا رو در شکل دیدم و بسیار فیض بردم.
اگر RQ دایره را در M و N قطع کند داریم : M وسط کمان AC و N وسط کمان AB است(چرا؟)
اگر P محل تماس دایره ی محاطی با BC باشد داریم : BM و PQ و ST در K همرسند و PR و CN و ST در L همرسند.
داریم : KL موازی BC است پس :CPQ=LKP=PRQ (زاویه) پس RQKL محاطی است پس DK×KL=DQ×DR .
TMNS محاطی است پس : DT×DS=DM×DN و از طرفی داریم : CLK=BCI=BMN (زاویه) پس NLKM محاطی است پس : DM×DN=DK×DL .
حال از این سه رابطه ( DK×KL=DQ×DR و DT×DS=DM×DN و DM×DN=DK×DL ) نتیجه میگیریم : DQ×DR=DT×DS پس : SRQT محاطی است.
سوال خیلی باحالی بود حدود 5 ساعت روش فکر کردم و خدا رو در شکل دیدم و بسیار فیض بردم.
پیوست ها
-
27.6 کیلوبایت بازدیدها 91