ماراتن هندسه
ba arze salam & khaste nabashid & dastmarizad be hame!
ba halle soale zibaye zir, soale 5tun ham kheili ghashang hal mishe:
khatte L zelhaye BC, CA, AB az mosallase ABC ra be tartib dar M, N, P ghat'e mikone. X, Y, Z be tartib markazhaye dayerehaye mohiti'e mosallashaye ANP, BPM ,CMN hastand. sabet konid markaz ertefaei'e mosallase XYZ, ruye jhatte L gharar darad
ba halle soale zibaye zir, soale 5tun ham kheili ghashang hal mishe:
khatte L zelhaye BC, CA, AB az mosallase ABC ra be tartib dar M, N, P ghat'e mikone. X, Y, Z be tartib markazhaye dayerehaye mohiti'e mosallashaye ANP, BPM ,CMN hastand. sabet konid markaz ertefaei'e mosallase XYZ, ruye jhatte L gharar darad
Eskandari گفت
ba arze salam & khaste nabashid & dastmarizad be hame!
ba halle soale zibaye zir, soale 5tun ham kheili ghashang hal mishe:
khatte L zelhaye BC, CA, AB az mosallase ABC ra be tartib dar M, N, P ghat'e mikone. X, Y, Z be tartib markazhaye dayerehaye mohiti'e mosallashaye AYZ, BZX ,CXY hastand. sabet konid markaz ertefaei'e mosallase XYZ, ruye jhatte L gharar darad
ba halle soale zibaye zir, soale 5tun ham kheili ghashang hal mishe:
khatte L zelhaye BC, CA, AB az mosallase ABC ra be tartib dar M, N, P ghat'e mikone. X, Y, Z be tartib markazhaye dayerehaye mohiti'e mosallashaye AYZ, BZX ,CXY hastand. sabet konid markaz ertefaei'e mosallase XYZ, ruye jhatte L gharar darad
صورت سؤالت رو یه بار دیگه چک می کنی!
hr_maleki گفت
Eskandari گفت
ba arze salam & khaste nabashid & dastmarizad be hame!
ba halle soale zibaye zir, soale 5tun ham kheili ghashang hal mishe:
khatte L zelhaye BC, CA, AB az mosallase ABC ra be tartib dar M, N, P ghat'e mikone. X, Y, Z be tartib markazhaye dayerehaye mohiti'e mosallashaye AYZ, BZX ,CXY hastand. sabet konid markaz ertefaei'e mosallase XYZ, ruye jhatte L gharar darad
ba halle soale zibaye zir, soale 5tun ham kheili ghashang hal mishe:
khatte L zelhaye BC, CA, AB az mosallase ABC ra be tartib dar M, N, P ghat'e mikone. X, Y, Z be tartib markazhaye dayerehaye mohiti'e mosallashaye AYZ, BZX ,CXY hastand. sabet konid markaz ertefaei'e mosallase XYZ, ruye jhatte L gharar darad
صورت سؤالت رو یه بار دیگه چک می کنی!
- ارسال ها
- 46
- لایک ها
- 0
- امتیاز
- 0
سلام
امیدوارم این کار قشنگتون ادامه پیدا کنه اما به شرط این که فقط در صورت حل سوال قبلی سوال جدید گذاشته بشه!
حالا اون سوال قشنگ آقای seifi :
برای حل این سوال ثابت کردم که مرکز دایره ی محیطی BQC روی PQ قرار داره ( خواهش میکنم اثبات اینو ازم نخواید چون تایپش یه کار بیچاره کنندیه اونم واسه ی من با این سرعت تایپ بالام )
حالا اگه از Q بر BC عمود کنیم تا BC رو در L قطع کنه مسلما" مرکز ارتفاعی BQC روی QL قرار خواهد داشت
پس میشه نتیجه گرفت که BQL = PQC (زاویه)
ازطرفی اگر PQ و AD در T متقاطع باشند داریم که AQT = PQC
این بدین معنی است که BQL = AQT (چه قدر ادبی شد)
چون TAQ = QBL (چهارضلعی محاطیه ) پس ATQ هم 90 درجه است
حالا اگه فکر میکنید بقیه سوالا حل شده یه پیغام بذارید تا این دفعه من یه سوال بذارم
امیدوارم این کار قشنگتون ادامه پیدا کنه اما به شرط این که فقط در صورت حل سوال قبلی سوال جدید گذاشته بشه!
حالا اون سوال قشنگ آقای seifi :
برای حل این سوال ثابت کردم که مرکز دایره ی محیطی BQC روی PQ قرار داره ( خواهش میکنم اثبات اینو ازم نخواید چون تایپش یه کار بیچاره کنندیه اونم واسه ی من با این سرعت تایپ بالام )
حالا اگه از Q بر BC عمود کنیم تا BC رو در L قطع کنه مسلما" مرکز ارتفاعی BQC روی QL قرار خواهد داشت
پس میشه نتیجه گرفت که BQL = PQC (زاویه)
ازطرفی اگر PQ و AD در T متقاطع باشند داریم که AQT = PQC
این بدین معنی است که BQL = AQT (چه قدر ادبی شد)
چون TAQ = QBL (چهارضلعی محاطیه ) پس ATQ هم 90 درجه است
حالا اگه فکر میکنید بقیه سوالا حل شده یه پیغام بذارید تا این دفعه من یه سوال بذارم
- ارسال ها
- 335
- لایک ها
- 8
- امتیاز
- 0
sabbasizadeh گفت
سلام
امیدوارم این کار قشنگتون ادامه پیدا کنه اما به شرط این که فقط در صورت حل سوال قبلی سوال جدید گذاشته بشه!
حالا اون سوال قشنگ آقای seifi :
برای حل این سوال ثابت کردم که مرکز دایره ی محیطی BQC روی PQ قرار داره ( خواهش میکنم اثبات اینو ازم نخواید چون تایپش یه کار بیچاره کنندیه اونم واسه ی من با این سرعت تایپ بالام )
حالا اگه از Q بر BC عمود کنیم تا BC رو در L قطع کنه مسلما" مرکز ارتفاعی BQC روی QL قرار خواهد داشت
پس میشه نتیجه گرفت که BQL = PQC (زاویه)
ازطرفی اگر PQ و AD در T متقاطع باشند داریم که AQT = PQC
این بدین معنی است که BQL = AQT (چه قدر ادبی شد)
چون TAQ = QBL (چهارضلعی محاطیه ) پس ATQ هم 90 درجه است
حالا اگه فکر میکنید بقیه سوالا حل شده یه پیغام بذارید تا این دفعه من یه سوال بذارم
امیدوارم این کار قشنگتون ادامه پیدا کنه اما به شرط این که فقط در صورت حل سوال قبلی سوال جدید گذاشته بشه!
حالا اون سوال قشنگ آقای seifi :
برای حل این سوال ثابت کردم که مرکز دایره ی محیطی BQC روی PQ قرار داره ( خواهش میکنم اثبات اینو ازم نخواید چون تایپش یه کار بیچاره کنندیه اونم واسه ی من با این سرعت تایپ بالام )
حالا اگه از Q بر BC عمود کنیم تا BC رو در L قطع کنه مسلما" مرکز ارتفاعی BQC روی QL قرار خواهد داشت
پس میشه نتیجه گرفت که BQL = PQC (زاویه)
ازطرفی اگر PQ و AD در T متقاطع باشند داریم که AQT = PQC
این بدین معنی است که BQL = AQT (چه قدر ادبی شد)
چون TAQ = QBL (چهارضلعی محاطیه ) پس ATQ هم 90 درجه است
حالا اگه فکر میکنید بقیه سوالا حل شده یه پیغام بذارید تا این دفعه من یه سوال بذارم
اثبات قشنگی بود ولی اثبات آسون تر داره.
پای عمود وارد از M برDB را E و پای عمود وارد از N بر AC را F بنامید با توجه به تشابه ABQ و DCQ و اینکه M,N وسطند ثابت میشود
دو مثلث BMQ , CNQ متشابه اند و چون ME و NF ارتفاعند بدست میاید دو مثلث BME و CNF متشابه اند و با نوشتن نسبت تشابه بدست
میاید : BE/CF=BM/CN=AB/DC=BQ/CQ پس EF با BC موازی است. پس QEF=QBC=QAD (زاویه) و اگر T محل برخورد PQ با AD باشد
داریم :AQT=PQF=FEP (زاویه) پس DAQ+AQT=QEF+PEF=90 پس PQ عمود است بر AD و اثبات کامل شد... .
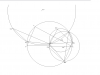
dar shekl zir noghteye barkhord AD ba BC ra ba A' va noghteye barkhorde AE ba BD ra B' namidim.
az anjayii ke AB' || BA' be rahati sabet mishavad ke (ADB') va (BDA') bar ham momase kharejand.
ma ye jurayi aks masale ro esbat mikonim va be rahati esbat mishavad ke un tarafe masale ham doroste(albate man in mozu ro be dalile badihi budanesh) esbat nakardam.
ebteda momase moshtarake in do dayere(ke az D migozarad) ro mikeshim.yani sabet mikonim baraye har noghteye P do zaviyeye ADE va BDC ba ham barabarand.
baraye in kar kafiye ke ye bar rabeteye AE/EB'=sin(ABE)/sin(EBB') . AB/BB' ro dar nazar begirim. va rabeteye motashabehe un ro yani BC/CA'=sin(BAC)/sin(CAA') . AB/AA' .hala kafiye esbat beshe
AE/EB'=BC/CA' yani sabet beshe sin(ABE)/sin(EBB') . sin(CAA')/sin(BAC) = BB'/AA' ke be dalile rabeteye ceva be surate
sinusi baraye se hamrase BP,AP,DP badihi ast+tashabohe ADB' va BDA' . h :
az anjayii ke AB' || BA' be rahati sabet mishavad ke (ADB') va (BDA') bar ham momase kharejand.
ma ye jurayi aks masale ro esbat mikonim va be rahati esbat mishavad ke un tarafe masale ham doroste(albate man in mozu ro be dalile badihi budanesh) esbat nakardam.
ebteda momase moshtarake in do dayere(ke az D migozarad) ro mikeshim.yani sabet mikonim baraye har noghteye P do zaviyeye ADE va BDC ba ham barabarand.
baraye in kar kafiye ke ye bar rabeteye AE/EB'=sin(ABE)/sin(EBB') . AB/BB' ro dar nazar begirim. va rabeteye motashabehe un ro yani BC/CA'=sin(BAC)/sin(CAA') . AB/AA' .hala kafiye esbat beshe
AE/EB'=BC/CA' yani sabet beshe sin(ABE)/sin(EBB') . sin(CAA')/sin(BAC) = BB'/AA' ke be dalile rabeteye ceva be surate
sinusi baraye se hamrase BP,AP,DP badihi ast+tashabohe ADB' va BDA' . h :
پیوست ها
-
27.3 کیلوبایت بازدیدها 104
- ارسال ها
- 335
- لایک ها
- 8
- امتیاز
- 0
سوال زیبایی بود!!!!
I را محل برخورد دایره ی OO[SUB]A[/SUB]M[SUB]A[/SUB] با دایره ی محیطی OO[SUB]C[/SUB]M[SUB]C[/SUB] مینامیم.داریم OIM[SUB]A[/SUB]= O[SUB]A[/SUB]OM[SUB]A[/SUB]+OM[SUB]A[/SUB]O[SUB]A[/SUB] و OIM[SUB]C[/SUB]=OO[SUB]C[/SUB]M[SUB]C[/SUB] (زاویه)
پس M[SUB]A[/SUB]IM[SUB]C[/SUB] = M[SUB]A[/SUB]IO+M[SUB]C[/SUB]IO = O[SUB]A[/SUB]OM[SUB]A[/SUB]+O[SUB]A[/SUB]M[SUB]A[/SUB]O+OO[SUB]C[/SUB]M[SUB]C [/SUB] (زاویه) و برای این که ثابت کنیم این دو دایره روی دایره ی محیطی
ABC همرسندباید ثابت کنیم زاویه ی M[SUB]A[/SUB]IM[SUB]C[/SUB] برابر کمان M[SUB]C[/SUB]M[SUB]A[/SUB] است که این کمان هم برابر زاویه ی B است.
حال H را مرکز ارتفاعی ABC مینامیم و L را محل برخورد CH و AO مینامیم .
چون OO[SUB]A[/SUB]=AH و OM[SUB]A[/SUB]=AO و اینکه AH موازی OO[SUB]A[/SUB] است بدست میاید دو مثلث AHO و OO[SUB]A[/SUB]M[SUB]A[/SUB] با هم برابرند
و به همین ترتیب دو مثلث OO[SUB]C[/SUB]M[SUB]C[/SUB] و COH با هم برابرند. پس O[SUB]A[/SUB]OM[SUB]A[/SUB] = HAO = B-C و OM[SUB]A[/SUB]O[SUB]A[/SUB] = AOH و OO[SUB]C[/SUB]M[SUB]C[/SUB] = CHO (زاویه)
پس
M[SUB]A[/SUB]IM[SUB]C[/SUB] = O[SUB]A[/SUB]OM[SUB]A[/SUB]+O[SUB]A[/SUB]M[SUB]A[/SUB]O+OO[SUB]C[/SUB]M[SUB]C[/SUB] = HAO+AOH+CHO = (B-C)+CLO=(B-C)+(OAC+OCA)=B-C+(90-B)+(90-A)=180-A-C=B
که این همان حکم مساله است. و به همین ترتیب ثابت میشود دایره ی دیگر هم با این دوتا روی دایره ی محیطی ABC همرسند.
و اثبات کامل شد... .

I را محل برخورد دایره ی OO[SUB]A[/SUB]M[SUB]A[/SUB] با دایره ی محیطی OO[SUB]C[/SUB]M[SUB]C[/SUB] مینامیم.داریم OIM[SUB]A[/SUB]= O[SUB]A[/SUB]OM[SUB]A[/SUB]+OM[SUB]A[/SUB]O[SUB]A[/SUB] و OIM[SUB]C[/SUB]=OO[SUB]C[/SUB]M[SUB]C[/SUB] (زاویه)
پس M[SUB]A[/SUB]IM[SUB]C[/SUB] = M[SUB]A[/SUB]IO+M[SUB]C[/SUB]IO = O[SUB]A[/SUB]OM[SUB]A[/SUB]+O[SUB]A[/SUB]M[SUB]A[/SUB]O+OO[SUB]C[/SUB]M[SUB]C [/SUB] (زاویه) و برای این که ثابت کنیم این دو دایره روی دایره ی محیطی
ABC همرسندباید ثابت کنیم زاویه ی M[SUB]A[/SUB]IM[SUB]C[/SUB] برابر کمان M[SUB]C[/SUB]M[SUB]A[/SUB] است که این کمان هم برابر زاویه ی B است.
حال H را مرکز ارتفاعی ABC مینامیم و L را محل برخورد CH و AO مینامیم .
چون OO[SUB]A[/SUB]=AH و OM[SUB]A[/SUB]=AO و اینکه AH موازی OO[SUB]A[/SUB] است بدست میاید دو مثلث AHO و OO[SUB]A[/SUB]M[SUB]A[/SUB] با هم برابرند
و به همین ترتیب دو مثلث OO[SUB]C[/SUB]M[SUB]C[/SUB] و COH با هم برابرند. پس O[SUB]A[/SUB]OM[SUB]A[/SUB] = HAO = B-C و OM[SUB]A[/SUB]O[SUB]A[/SUB] = AOH و OO[SUB]C[/SUB]M[SUB]C[/SUB] = CHO (زاویه)
پس
M[SUB]A[/SUB]IM[SUB]C[/SUB] = O[SUB]A[/SUB]OM[SUB]A[/SUB]+O[SUB]A[/SUB]M[SUB]A[/SUB]O+OO[SUB]C[/SUB]M[SUB]C[/SUB] = HAO+AOH+CHO = (B-C)+CLO=(B-C)+(OAC+OCA)=B-C+(90-B)+(90-A)=180-A-C=B
که این همان حکم مساله است. و به همین ترتیب ثابت میشود دایره ی دیگر هم با این دوتا روی دایره ی محیطی ABC همرسند.
و اثبات کامل شد... .

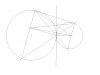
@ sabbasizadeh :
javabetun ro tuye tasvire avali bebinid...
@seifi_seifi:
badihist ke DAC=90
hala kafiye ke ye davaran be markaze D va c bezanid ta M ro be B va badesh B ro be N tabdil konin.
sepas be dalile ghaziyey tarkib do davaran in masale un ghadr asun hal mishe ke dige ehtiyaji be tozih nist.
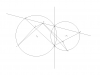
حالت کلی این مسئله رو حل کنید:
فرض کنید که دو دایره ی O_1 و O_2 هم دیگر را در A و B قطع کنند.خطی دلخواه از A بگذرانید تا دو دایره را در نقاط C و D قطع کند.
نقطه ی دلخواه M را روی پاره خط CD در نظر بگیرید و از آن به موازات CB و DB خط بکشید تا DB و CB را در نقاط E و F قطع کنند.
از E و F عمود را بر ضلع هایی که روی آن واقع اند رسم کنید تا مطابق شکل دو دایره را در X و Y قطع کنند.ثابت کنید که XMY=90° .
javabetun ro tuye tasvire avali bebinid...
@seifi_seifi:
badihist ke DAC=90
hala kafiye ke ye davaran be markaze D va c bezanid ta M ro be B va badesh B ro be N tabdil konin.
sepas be dalile ghaziyey tarkib do davaran in masale un ghadr asun hal mishe ke dige ehtiyaji be tozih nist.
حالت کلی این مسئله رو حل کنید:
فرض کنید که دو دایره ی O_1 و O_2 هم دیگر را در A و B قطع کنند.خطی دلخواه از A بگذرانید تا دو دایره را در نقاط C و D قطع کند.
نقطه ی دلخواه M را روی پاره خط CD در نظر بگیرید و از آن به موازات CB و DB خط بکشید تا DB و CB را در نقاط E و F قطع کنند.
از E و F عمود را بر ضلع هایی که روی آن واقع اند رسم کنید تا مطابق شکل دو دایره را در X و Y قطع کنند.ثابت کنید که XMY=90° .
پیوست ها
-
25.8 کیلوبایت بازدیدها 57
-
179.2 کیلوبایت بازدیدها 56