ماراتن هندسه
- ارسال ها
- 335
- لایک ها
- 8
- امتیاز
- 0
shoki گفت
@ sabbasizadeh :
javabetun ro tuye tasvire avali bebinid...
@seifi_seifi:
badihist ke DAC=90
hala kafiye ke ye davaran be markaze D va c bezanid ta M ro be B va badesh B ro be N tabdil konin.
sepas be dalile ghaziyey tarkib do davaran in masale un ghadr asun hal mishe ke dige ehtiyaji be tozih nist.
حالت کلی این مسئله رو حل کنید:
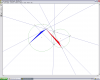
فرض کنید که دو دایره ی O_1 و O_2 هم دیگر را در A و B قطع کنند.خطی دلخواه از A بگذرانید تا دو دایره را در نقاط C و D قطع کند.
نقطه ی دلخواه M را روی پاره خط CD در نظر بگیرید و از آن به موازات CB و DB خط بکشید تا DB و CB را در نقاط E و F قطع کنند.
از E و F عمود را بر ضلع هایی که روی آن واقع اند رسم کنید تا مطابق شکل دو دایره را در X و Y قطع کنند.ثابت کنید که XMY=90° .
javabetun ro tuye tasvire avali bebinid...
@seifi_seifi:
badihist ke DAC=90
hala kafiye ke ye davaran be markaze D va c bezanid ta M ro be B va badesh B ro be N tabdil konin.
sepas be dalile ghaziyey tarkib do davaran in masale un ghadr asun hal mishe ke dige ehtiyaji be tozih nist.
حالت کلی این مسئله رو حل کنید:
فرض کنید که دو دایره ی O_1 و O_2 هم دیگر را در A و B قطع کنند.خطی دلخواه از A بگذرانید تا دو دایره را در نقاط C و D قطع کند.
نقطه ی دلخواه M را روی پاره خط CD در نظر بگیرید و از آن به موازات CB و DB خط بکشید تا DB و CB را در نقاط E و F قطع کنند.
از E و F عمود را بر ضلع هایی که روی آن واقع اند رسم کنید تا مطابق شکل دو دایره را در X و Y قطع کنند.ثابت کنید که XMY=90° .
دمت گرم راه حلت خیلی آسون بود و راه من خیلی سخت بود.

- ارسال ها
- 46
- لایک ها
- 0
- امتیاز
- 0
حالا که بحث رفت سراغ دوران و این حرفا بذارین یه سوال قشنگ و کاربردی دیگه هم امروز بدیم تا فعالترین روز این تاپیک رو تجربه کنیم:
قضیه پمپیو:
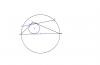
در هر مثلث متساوی الاضلاع ABC برای هر نقطه ی P که روی دایره محیطی قرار نداشته باشد می توان یک مثلث با اضلاع AP,BP,CP ساخت.
اگر P روی دایره محیطی باشد هم مجموع دو تا از اینها با دیگری برابر میشه.
قضیه پمپیو:
در هر مثلث متساوی الاضلاع ABC برای هر نقطه ی P که روی دایره محیطی قرار نداشته باشد می توان یک مثلث با اضلاع AP,BP,CP ساخت.
اگر P روی دایره محیطی باشد هم مجموع دو تا از اینها با دیگری برابر میشه.
esbatesh in payin umade..
chon esbate man ham mesle hamine va kheyli tanbalam in karo kardam..
dar vaghe faghat shekl ro ke bebinid
mifahid bayad chi kar kard
davaran be markaze C
baraye masaleye jadid:
ba haman farzhaye ghabli makan hendesiye noghate P ra biyabid ke masahate mosalase tashkil shode tavasote mosalase be azla-e PA,PB,PC barabare meghdari sabet bashe.
@sabbasizadeh:
inboxetun ro check konid
chon esbate man ham mesle hamine va kheyli tanbalam in karo kardam..
dar vaghe faghat shekl ro ke bebinid
mifahid bayad chi kar kard
davaran be markaze C
baraye masaleye jadid:
ba haman farzhaye ghabli makan hendesiye noghate P ra biyabid ke masahate mosalase tashkil shode tavasote mosalase be azla-e PA,PB,PC barabare meghdari sabet bashe.
@sabbasizadeh:
inboxetun ro check konid
پیوست ها
-
17.5 کیلوبایت بازدیدها 162
- ارسال ها
- 335
- لایک ها
- 8
- امتیاز
- 0
مکان هندسی نقطه ی P میشود دایره ای به مرکز O که O مرکز دایره ی محیطی ABC است.
ثابت میکنیم مساحت مثلث با اضلاع PA,PB,PC برابر است با sin60)/3) .(a[SUP]2[/SUP]-3d[SUP]2[/SUP])i)) که a طول ضلع و d فاصله ی P از O است.
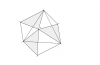
مثلث ABM را حول A به اندازه ی 60 درجه دوران میدهیم و همین کار را برای دو مثلث دیگر هم انجام میدهیم.
مساحت شش ضلعی ایجاد شده دو برابر مساحت مثلث است و مساحت سه شکل هاشور خورده باهم برابر است و 3 برابر مساحت
مثلث است که با PA,PB,PC ساخته میشود. و آن سه مثلث هاشور نخورده متساوی الاضلاع هستند و از اینجا به بعد فقط محاسبات است
و بقیه اش را خودتان بروید چون کاری نداره و فقط تو محاسبه ی مجموع سه مساحت مثلث های هاشور نخورده از لایبنیتس استفاده میشه.
ثابت میکنیم مساحت مثلث با اضلاع PA,PB,PC برابر است با sin60)/3) .(a[SUP]2[/SUP]-3d[SUP]2[/SUP])i)) که a طول ضلع و d فاصله ی P از O است.
مثلث ABM را حول A به اندازه ی 60 درجه دوران میدهیم و همین کار را برای دو مثلث دیگر هم انجام میدهیم.
مساحت شش ضلعی ایجاد شده دو برابر مساحت مثلث است و مساحت سه شکل هاشور خورده باهم برابر است و 3 برابر مساحت
مثلث است که با PA,PB,PC ساخته میشود. و آن سه مثلث هاشور نخورده متساوی الاضلاع هستند و از اینجا به بعد فقط محاسبات است
و بقیه اش را خودتان بروید چون کاری نداره و فقط تو محاسبه ی مجموع سه مساحت مثلث های هاشور نخورده از لایبنیتس استفاده میشه.
پیوست ها
-
27.3 کیلوبایت بازدیدها 132
[font=Tahoma,sans-serif][FONT=Tahoma,sans-serif][FONT=Tahoma,sans-serif][/font][/FONT][/FONT]
[font=Tahoma,sans-serif][FONT=Tahoma,sans-serif][FONT=Tahoma,sans-serif]masale be rahati hal mishe[/font][/FONT][/FONT][font=Tahoma,sans-serif][FONT=Tahoma,sans-serif][FONT=Tahoma,sans-serif]...
az O ye khate movazi ba BP bekeshid va chon in khat az vasate CP migzare pas agar dar noghteye S' ba EF barkhord kone be dalile ghaziyeye maruf BS' mishavad nimsaze zaviyeye PBC. va az tarafi digar ham chon CS' bar BS' amud ast va BC ghotr pas S' ruye dayere ast.
yani esbat shod S' = S .
be hamin tartib R' = R. [/font]
va darnatije OS || PB va OR ||PC yani SOR=APB. [font=Tahoma,sans-serif]
[/font]va hokm esbat mishavad.
[font=Tahoma,sans-serif]masaleye badi...
in masale ro chand vaghte pish MeysamS ferestadand vaman ham tamimesho az shoma mikham...
dar mosalsea AMN yek khat AM va AN ra dar P va Q ghat mikonad
P va Q ra nesbate be M va N gharine mikonim ta B va C be dast ayad.
hal farz konid ke G ,G',G'' marakezze seghle APQ,AMN,ABC be tartib bashand.
O,O',O'' be tartib moshabeh baraye marakeze davayere mohiti tarif mishavand.
hala esbat konid agar noghate X,X',X'' be gunei ruye OG,O'G',O''G'' bashand ke OX/GX=O'X'/G'X'=O''X''/G''X'' angah X,X',X'' hamkhatand.
[/font]
[/FONT]
[/FONT]
[font=Tahoma,sans-serif][FONT=Tahoma,sans-serif][FONT=Tahoma,sans-serif]masale be rahati hal mishe[/font][/FONT][/FONT][font=Tahoma,sans-serif][FONT=Tahoma,sans-serif][FONT=Tahoma,sans-serif]...
az O ye khate movazi ba BP bekeshid va chon in khat az vasate CP migzare pas agar dar noghteye S' ba EF barkhord kone be dalile ghaziyeye maruf BS' mishavad nimsaze zaviyeye PBC. va az tarafi digar ham chon CS' bar BS' amud ast va BC ghotr pas S' ruye dayere ast.
yani esbat shod S' = S .
be hamin tartib R' = R. [/font]
va darnatije OS || PB va OR ||PC yani SOR=APB. [font=Tahoma,sans-serif]
[/font]va hokm esbat mishavad.
[font=Tahoma,sans-serif]masaleye badi...
in masale ro chand vaghte pish MeysamS ferestadand vaman ham tamimesho az shoma mikham...
dar mosalsea AMN yek khat AM va AN ra dar P va Q ghat mikonad
P va Q ra nesbate be M va N gharine mikonim ta B va C be dast ayad.
hal farz konid ke G ,G',G'' marakezze seghle APQ,AMN,ABC be tartib bashand.
O,O',O'' be tartib moshabeh baraye marakeze davayere mohiti tarif mishavand.
hala esbat konid agar noghate X,X',X'' be gunei ruye OG,O'G',O''G'' bashand ke OX/GX=O'X'/G'X'=O''X''/G''X'' angah X,X',X'' hamkhatand.
[/font]
[/FONT]
[/FONT]
پیوست ها
-
42.2 کیلوبایت بازدیدها 67
- ارسال ها
- 335
- لایک ها
- 8
- امتیاز
- 0
سوال جالبی بود.
لم 1 : در چهار ضلعی ABCD نقطه ی E روی AB و F روی DC قرار دارد به طوری که AE/EB=DF/FC=a آنگاه بردار
AD × 1/(a+1) + BC × a/(a+1) = EF ( در این جا AD,BC,EF بردار هستند و a عددی اسکالر است.)(اثبات ساده است)
لم 2 :نقاط A,B,C سه نقطه داخل زاویه ی xOy قرار دارند و A[SUB]1[/SUB],B[SUB]1[/SUB],C[SUB]1[/SUB] پای عمود وارد از A,B,C بر یک ضلع و A[SUB]2[/SUB],B[SUB]2[/SUB],C[SUB]2[/SUB] پای عمود A,B,C
بر ضلع دیگر این زاویه است. A,B,C همخطند اگر و فقط اگر : A[SUB]1[/SUB]B[SUB]1[/SUB]/B[SUB]1[/SUB]C[SUB]1[/SUB]=A[SUB]2[/SUB]B[SUB]2[/SUB]/B[SUB]2[/SUB]C[SUB]2[/SUB] (اثبات ساده است)
حال با استفاده از این دو لم مساله را اثبات میکنیم.
طبق لم 1 اثبات میشود اوساط PQ,MN,BC روی یک خط میباشند پس Gو'G و "G هم خطند و 'G وسط "GG قرار دارند.
حال طبق لم 2 O و 'O و "O روی یک خطند و 'O وسط "OO است.
حال طبق لم 1 دو بردار 'XX و 'X"X همراستا و طول آنها برابر است.پس X و 'X و "X روی یک خط قرار دارند و 'X وسط "XX قرار دارد.
و اثبات کامل شد... .

لم 1 : در چهار ضلعی ABCD نقطه ی E روی AB و F روی DC قرار دارد به طوری که AE/EB=DF/FC=a آنگاه بردار
AD × 1/(a+1) + BC × a/(a+1) = EF ( در این جا AD,BC,EF بردار هستند و a عددی اسکالر است.)(اثبات ساده است)
لم 2 :نقاط A,B,C سه نقطه داخل زاویه ی xOy قرار دارند و A[SUB]1[/SUB],B[SUB]1[/SUB],C[SUB]1[/SUB] پای عمود وارد از A,B,C بر یک ضلع و A[SUB]2[/SUB],B[SUB]2[/SUB],C[SUB]2[/SUB] پای عمود A,B,C
بر ضلع دیگر این زاویه است. A,B,C همخطند اگر و فقط اگر : A[SUB]1[/SUB]B[SUB]1[/SUB]/B[SUB]1[/SUB]C[SUB]1[/SUB]=A[SUB]2[/SUB]B[SUB]2[/SUB]/B[SUB]2[/SUB]C[SUB]2[/SUB] (اثبات ساده است)
حال با استفاده از این دو لم مساله را اثبات میکنیم.
طبق لم 1 اثبات میشود اوساط PQ,MN,BC روی یک خط میباشند پس Gو'G و "G هم خطند و 'G وسط "GG قرار دارند.
حال طبق لم 2 O و 'O و "O روی یک خطند و 'O وسط "OO است.
حال طبق لم 1 دو بردار 'XX و 'X"X همراستا و طول آنها برابر است.پس X و 'X و "X روی یک خط قرار دارند و 'X وسط "XX قرار دارد.
و اثبات کامل شد... .

kafiye ke noghteye barkhordesh ro ba dayereye mohitiye AMN dar nazar begirim ke dar an M va N vasathaye AB va AC hastand ...
badesh agar noghteye barkhorde do dayere L bashe unvaght LFM va LEN be vozuh motashabehand(be halate tasaviye zavaya) va hala ba neveshtane ravabeteshun be dast miyad ...
LM/LN= FM/EN
va hal chon kasre FM/EN sabet hast (in mozu kheyli vazehe) dar natije jaygahe noghteye L ham sabet hast (yani yeki az noghate barkhorde dayereye applonius ba dayereye (AMN) hast) .pas hokm esbat mishavad...
hala ye masaleye jadid...
agar I_a markaze dayereye mohitiye kharejiye nazire rase A dar mosalase ABC bashad ve I_aF amud bar AB bashad va F ruye AB bashad angah sabet shavad vasate CF va vasate AB va I_a hamkhatand.
badesh agar noghteye barkhorde do dayere L bashe unvaght LFM va LEN be vozuh motashabehand(be halate tasaviye zavaya) va hala ba neveshtane ravabeteshun be dast miyad ...
LM/LN= FM/EN
va hal chon kasre FM/EN sabet hast (in mozu kheyli vazehe) dar natije jaygahe noghteye L ham sabet hast (yani yeki az noghate barkhorde dayereye applonius ba dayereye (AMN) hast) .pas hokm esbat mishavad...
hala ye masaleye jadid...
agar I_a markaze dayereye mohitiye kharejiye nazire rase A dar mosalase ABC bashad ve I_aF amud bar AB bashad va F ruye AB bashad angah sabet shavad vasate CF va vasate AB va I_a hamkhatand.
پیوست ها
-
26.5 کیلوبایت بازدیدها 44
- ارسال ها
- 335
- لایک ها
- 8
- امتیاز
- 0
لم : مکان هندسی نقاطی مانند M که S[SUB]MAB[/SUB]-S[SUB]MCD[/SUB]=K که K مقداری ثابت است خطی است موازی خطی که اوساط AD و BC را به هم
متصل میکند.
حال داریم : S[SUB]MAC[/SUB]-S[SUB]MBF[/SUB]=S[SUB]ABC[/SUB]/2 و از طرفی S[SUB]ACIa[/SUB]-S[SUB]BCIa[/SUB]=1/2r[SUB]a[/SUB](AC-BF)=1/2r[SUB]a[/SUB].(P-a)=1/2r×P/(P-a)×(P-a)=1/2rP=S/2
پس I[SUB]a[/SUB] روی خطی موازی MN قرار دارد که از M هم میگذرد که این خط همان MN است.
متصل میکند.
حال داریم : S[SUB]MAC[/SUB]-S[SUB]MBF[/SUB]=S[SUB]ABC[/SUB]/2 و از طرفی S[SUB]ACIa[/SUB]-S[SUB]BCIa[/SUB]=1/2r[SUB]a[/SUB](AC-BF)=1/2r[SUB]a[/SUB].(P-a)=1/2r×P/(P-a)×(P-a)=1/2rP=S/2
پس I[SUB]a[/SUB] روی خطی موازی MN قرار دارد که از M هم میگذرد که این خط همان MN است.
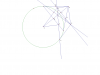
hamanande shekl noghat ra namgozari konid.
badihist ke (be dalile ghaziyeye ghotb o ghotbi) OA bar PE amud ast .
pas bayad sabet konim ke OA || PH. ama az anja ke X ruye ghotbiye E ast pas ghotbiye X az E migozarad va dar natije bar OX amud ast.
ama khate amud bar OX az E haman khate MN ast.
dar natije agar E ruye Mn harkat konad chon ghotbiye X ,MN mibashad pas X sabet hast.
yani nesbat XO/XP va az tarafi ham XB/XC sabet hast.
hal baraye tavaziye OA va PH kafist sabet shavad ke XO/XP= XA/XH va chon XA/XH= XB/XC pas kafits sabet shavad
XO /XP = XB/XC ke az inja be bad faghat ye seri mohasebat dar pish ast...
@seifi_seifi:
tuye rahe haletun ye jayi ro eshtebahi type kardind.hamun khate aval bayad nevesht S_{MAC}-S_{MBF}=S_{ABC} /2 .
vali az rahe hale ghashangetun mamnunam.
masaleye badi...
dar mosalase ABC dayereye mohatiye dakheli dar D,E,F bar BC,CA,AB momas ast.
AD dayereye mohati ra dar S ghat mikonad va BS,CS dayereye mohati ra dar P,Q ghat mikonand .
sabet konid ke FP,EQ,AD hamrasand.
badihist ke (be dalile ghaziyeye ghotb o ghotbi) OA bar PE amud ast .
pas bayad sabet konim ke OA || PH. ama az anja ke X ruye ghotbiye E ast pas ghotbiye X az E migozarad va dar natije bar OX amud ast.
ama khate amud bar OX az E haman khate MN ast.
dar natije agar E ruye Mn harkat konad chon ghotbiye X ,MN mibashad pas X sabet hast.
yani nesbat XO/XP va az tarafi ham XB/XC sabet hast.
hal baraye tavaziye OA va PH kafist sabet shavad ke XO/XP= XA/XH va chon XA/XH= XB/XC pas kafits sabet shavad
XO /XP = XB/XC ke az inja be bad faghat ye seri mohasebat dar pish ast...
@seifi_seifi:
tuye rahe haletun ye jayi ro eshtebahi type kardind.hamun khate aval bayad nevesht S_{MAC}-S_{MBF}=S_{ABC} /2 .
vali az rahe hale ghashangetun mamnunam.
masaleye badi...
dar mosalase ABC dayereye mohatiye dakheli dar D,E,F bar BC,CA,AB momas ast.
AD dayereye mohati ra dar S ghat mikonad va BS,CS dayereye mohati ra dar P,Q ghat mikonand .
sabet konid ke FP,EQ,AD hamrasand.
پیوست ها
-
41.3 کیلوبایت بازدیدها 151
-
35.9 کیلوبایت بازدیدها 151
- ارسال ها
- 335
- لایک ها
- 8
- امتیاز
- 0
shoki گفت
hamanande shekl noghat ra namgozari konid.
badihist ke (be dalile ghaziyeye ghotb o ghotbi) OA bar PE amud ast .
pas bayad sabet konim ke OA || PH. ama az anja ke X ruye ghotbiye E ast pas ghotbiye X az E migozarad va dar natije bar OX amud ast.
ama khate amud bar OX az E haman khate MN ast.
dar natije agar E ruye Mn harkat konad chon ghotbiye X ,MN mibashad pas X sabet hast.
yani nesbat XO/XP va az tarafi ham XB/XC sabet hast.
hal baraye tavaziye OA va PH kafist sabet shavad ke XO/XP= XA/XH va chon XA/XH= XB/XC pas kafits sabet shavad
XO /XP = XB/XC ke az inja be bad faghat ye seri mohasebat dar pish ast...
.
badihist ke (be dalile ghaziyeye ghotb o ghotbi) OA bar PE amud ast .
pas bayad sabet konim ke OA || PH. ama az anja ke X ruye ghotbiye E ast pas ghotbiye X az E migozarad va dar natije bar OX amud ast.
ama khate amud bar OX az E haman khate MN ast.
dar natije agar E ruye Mn harkat konad chon ghotbiye X ,MN mibashad pas X sabet hast.
yani nesbat XO/XP va az tarafi ham XB/XC sabet hast.
hal baraye tavaziye OA va PH kafist sabet shavad ke XO/XP= XA/XH va chon XA/XH= XB/XC pas kafits sabet shavad
XO /XP = XB/XC ke az inja be bad faghat ye seri mohasebat dar pish ast...
.
نقطه ی P یک دایره به شعاع 0 است و MN محور اصلی آن است و قوت E نسبت به نقطه و دایره برابر است پس EF=EG=EP
پس E مرکز دایره ی محیطی DFG است حال محور اصلی های دایره ی داده شده و دایره ی PFG و دایره P (نقطه) همرسند که
که محور اصلی دایره ی داده شده و دایره یPFG همان FG است و محور اصلی نقطه ی P و دایره ی داده شده همان MN است و محور
اصلی نقطه ی P و دایره ی PFG مماس در P است که این سه در H همرسند پس PH بر دایره ی محیطی PFG مماس است پس
EDH=90
- ارسال ها
- 335
- لایک ها
- 8
- امتیاز
- 0
در مثلث ASB برای قاطع FP منلائوس مینویسیم و یک بار در مثلث ASC برای قاطع EQ منلائوس مینویسیم و سپس با برابر قرار دادن دو
عبارت حاصل از نوشتن منلائوس ها بدست میاید که باید SQ/QC × EC/FB × BP/PS =1 و این معادل همرسی سه خط AD,BQ,CP است و
این مساله هم که این سه خط همرسند سوال مرحله سوم ایران در چند سال گذشته بوده است و برای اثبات این ابتدا ثابت میکنیم
AD,BE,CF همرسند (با سوا) و سپس ثابت میکنیم نسبت ناهمساز چهار پرتو BS,BE,BQ,BC با نسبت ناهمساز چهار پرتو CS,CF,CP,CB
برابر است (اثباتش رو از من نخواهید که طولانی است و نوشتنش خیلی سخته) و آنگاه چون پرتو BC مشترک است بدست میاید که D و
محل برخورد EB,CF و محل برخورد BQ,CP همخطند که این هم معادل همرسیAD,BQ,CP است.
اگه میشه shoki راه حل خودتو هم بنویس چون راه من یه جوریه ... .

عبارت حاصل از نوشتن منلائوس ها بدست میاید که باید SQ/QC × EC/FB × BP/PS =1 و این معادل همرسی سه خط AD,BQ,CP است و
این مساله هم که این سه خط همرسند سوال مرحله سوم ایران در چند سال گذشته بوده است و برای اثبات این ابتدا ثابت میکنیم
AD,BE,CF همرسند (با سوا) و سپس ثابت میکنیم نسبت ناهمساز چهار پرتو BS,BE,BQ,BC با نسبت ناهمساز چهار پرتو CS,CF,CP,CB
برابر است (اثباتش رو از من نخواهید که طولانی است و نوشتنش خیلی سخته) و آنگاه چون پرتو BC مشترک است بدست میاید که D و
محل برخورد EB,CF و محل برخورد BQ,CP همخطند که این هم معادل همرسیAD,BQ,CP است.
اگه میشه shoki راه حل خودتو هم بنویس چون راه من یه جوریه ... .

Faghat ghabl az khundanesh taghyire esmhaye zir ra anjam dahid:noghateye tamas az D be Z taghyir mikonad va S be P taghyir mikonad va P,Q be Y,X taghyir mikonad.baghiye naoghate ba haman esmhast.
Let
 be the touch points of the incircle (with center
be the touch points of the incircle (with center
 ) with
) with

then by using similarities (or directly the well-known theorem) we get
 and similarly
and similarly

now we get
 or in other words
or in other words
 which is in fact the sufficient and needed condition for which
which is in fact the sufficient and needed condition for which
 are concurrent(use céva's theorem sinus form for proving this).
are concurrent(use céva's theorem sinus form for proving this).
let the tangent at point
 to
to
 intersect
intersect
 at
at
 then by the well-known theorem(of pole and polar) we have the concurrency of
then by the well-known theorem(of pole and polar) we have the concurrency of
 at point
at point
 .(
.(
 is the tangent)
is the tangent)
also we know that
 and since
and since
 are collinear it implies the concurrency of
are collinear it implies the concurrency of
 and we are done
and we are done
agar har jayisho nafahmidid be man hatman begid...
rastesh in soalo chand vaghte pish tu mathlinks bud va man rahe halamo copy-paste kardam...
sharmande ke tarjomash nakardam..

Let



then by using similarities (or directly the well-known theorem) we get


now we get



let the tangent at point







also we know that



agar har jayisho nafahmidid be man hatman begid...
rastesh in soalo chand vaghte pish tu mathlinks bud va man rahe halamo copy-paste kardam...
sharmande ke tarjomash nakardam..