ماراتن هندسه
- ارسال ها
- 935
- لایک ها
- 1,654
- امتیاز
- 93
پاسخ : ماراتن هندسه
جواب سوال آقا ارس . @aras 2213
محل تماس دایره با اصلاع AB , AC رو به ترتیب F,D میگیریم .طبق قوانین همساز و ناهمساز نتیجه میگیریم که AZDK = -1
پس

از اونجایی که FZ موازی با PK هست . نتیجه میشه که

پس P , F , M هم خط اند و به طرز مشابه بدست میاد که Q , E , M هم خط اند
اگه محل برخورد دوم دایره با BC رو S بگیریم براحتی میشه نتیجه گرفت که S, K نسبت به وسط BC قرینه اند .
و میشه نتیجه گرفت که S وسط PQ است. پس مرکز دایره PQM روی خطی عمود بر PQ و گذرنده از S قرار دارد .
مرکز دایره محیطی QPM رو O' می نامیم و مرکز دایره FDM رو هم O مینامیم .
وسط FD رو هم N میگیریم


پس

چون ON , O'S هر دو موازی و عمود بر BC اند پس باید O , O' , M هم خط اند .
پس چون M یکی از محل های برخورد دو دایره هست پس چون دو دایره مماس اند .
جواب سوال آقا ارس . @aras 2213
محل تماس دایره با اصلاع AB , AC رو به ترتیب F,D میگیریم .طبق قوانین همساز و ناهمساز نتیجه میگیریم که AZDK = -1
پس
از اونجایی که FZ موازی با PK هست . نتیجه میشه که
پس P , F , M هم خط اند و به طرز مشابه بدست میاد که Q , E , M هم خط اند
اگه محل برخورد دوم دایره با BC رو S بگیریم براحتی میشه نتیجه گرفت که S, K نسبت به وسط BC قرینه اند .
و میشه نتیجه گرفت که S وسط PQ است. پس مرکز دایره PQM روی خطی عمود بر PQ و گذرنده از S قرار دارد .
مرکز دایره محیطی QPM رو O' می نامیم و مرکز دایره FDM رو هم O مینامیم .
وسط FD رو هم N میگیریم
پس
چون ON , O'S هر دو موازی و عمود بر BC اند پس باید O , O' , M هم خط اند .
پس چون M یکی از محل های برخورد دو دایره هست پس چون دو دایره مماس اند .
پاسخ : ماراتن هندسه
ae رو به اندازه خودش ادامه بدید(از سمت نقطه e) و نقطه انتهاییش رو g فرض کنید.پس مثلث acg متساوی الاساقین میشه. پس طبق فرض مثلث dcg با مثلث abd متشابهه و این یعنی dg=gc=ac. و حالا حکم بدیهیه.
سوال بعد( یه سوال آسون برای راه افتادن ماراتن):
 نیمساز مثلث
نیمساز مثلث
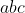 است و میدانیم
است و میدانیم
 . نقطه
. نقطه
 تصویر راس
تصویر راس
 بر خط
بر خط
 است. اثبات کنید
است. اثبات کنید

پاسخ : ماراتن هندسه
البته هنوز سوال آقاي پويا حل نشده است. هر كي حل كرد لطفا جوابشو بذاره. اينم سوال بعد:
فرض کنید دایره ی w به مرکز O دایره ی محیطی مثلث ABC باشد و
 . فرض کنید D محل برخورد خط AB با عمودی که در C بر ضلع AC وارد می شود باشد. خط l از نقطه ی D گذشته و بر AO عمود است. محل برخورد l و AC را E و محل برخورد l و دایره ی w را که بین E و D قرار دارد F می نامیم. ثابت کنید دایره های محیطی مثلث های BFE و CFD در نقطه ی F بر یکدیگر مماسند.
. فرض کنید D محل برخورد خط AB با عمودی که در C بر ضلع AC وارد می شود باشد. خط l از نقطه ی D گذشته و بر AO عمود است. محل برخورد l و AC را E و محل برخورد l و دایره ی w را که بین E و D قرار دارد F می نامیم. ثابت کنید دایره های محیطی مثلث های BFE و CFD در نقطه ی F بر یکدیگر مماسند.
سوال بعد( یه سوال آسون برای راه افتادن ماراتن):
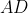 نیمساز مثلث
نیمساز مثلث
 است و میدانیم
است و میدانیم
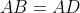 . نقطه
. نقطه
 تصویر راس
تصویر راس
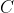 بر خط
بر خط
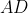 است. اثبات کنید
است. اثبات کنید

فرض کنید دایره ی w به مرکز O دایره ی محیطی مثلث ABC باشد و
پاسخ : ماراتن هندسه
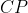 رو امتداد ميديم تا ضلع
رو امتداد ميديم تا ضلع
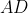 رو در
رو در
 قطع كنه. كافيه بگيم
قطع كنه. كافيه بگيم
 اما معادل اينه كه A,Q نسبت به نيمساز زاويه
اما معادل اينه كه A,Q نسبت به نيمساز زاويه
 مزدوج همزاويه باشند.اما اين معادل اينه كه P(EADB)=P(FQBD) چون مزدوج همزاويه كردن ناهمساز رو حفط ميكنه.فرض كنيد PB خطوط CD و AD رو در R و S قطع كنه. همچنين PE خط AD رو در T قطع ميكنه. پس P(EDAB)=(TDAS)=(PRBS)=(QDFS)=P(QDFB)=P(FQBD) كه همون حكم مساله است.
مزدوج همزاويه باشند.اما اين معادل اينه كه P(EADB)=P(FQBD) چون مزدوج همزاويه كردن ناهمساز رو حفط ميكنه.فرض كنيد PB خطوط CD و AD رو در R و S قطع كنه. همچنين PE خط AD رو در T قطع ميكنه. پس P(EDAB)=(TDAS)=(PRBS)=(QDFS)=P(QDFB)=P(FQBD) كه همون حكم مساله است.
---- دو نوشته به هم متصل شده است ----
سوال بعد: در مثلث ABC داريم AB=AC .نقطه D وسط BC است. E پاي عمود D بر AC است.F وسط DE است. ثابت كنيد AF بر BE عمود است.
ويرايش: راس متساوي الساقين رو اشتباها B گذاشته بودم.
مثلث رو ببرید تو دستگاه مختصات دکارتی. بدون این که خللی به مساله وارد بشه فرض کنید:
&space;,&space;B=(-1,0),C=(1,0),D=(0,0)) حالا به محاسبه نقطه
حالا به محاسبه نقطه
 میپردازیم که میشه:
میپردازیم که میشه:
) پس نقطه وسط
پس نقطه وسط
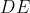 که
که
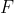 هست میشه:
هست میشه:
},\frac{a}{2(1+a^2)})) حالا برای بررسی حکم مساله کافیه داشته باشیم:
حالا برای بررسی حکم مساله کافیه داشته باشیم:
}}{0-\frac{a^2}{2(1+a^2)}}) و
و
 حاصل ضربشون بشه 1-که میشه!
حاصل ضربشون بشه 1-که میشه!
هر کدوم شیب خط هایی هستن که قراره بر هم عمود بشن.
در نتیجه مساله اثبات شده است.
---- دو نوشته به هم متصل شده است ----
سوال بعد: در مثلث ABC داريم AB=AC .نقطه D وسط BC است. E پاي عمود D بر AC است.F وسط DE است. ثابت كنيد AF بر BE عمود است.
ويرايش: راس متساوي الساقين رو اشتباها B گذاشته بودم.
هر کدوم شیب خط هایی هستن که قراره بر هم عمود بشن.
در نتیجه مساله اثبات شده است.
آخرین ویرایش توسط مدیر
پاسخ : ماراتن هندسه
محل برخورد CD و AO رو T بگیرید.به وضوح T رو w میفته.حالا E مرکز ارتفاعی مثلث ATD هست و TBA هم 90 است،پس T,E,B هم خطن.پس
 که این
که این
نتیجه میده دو دایره بر هم مماسند.
---- دو نوشته به هم متصل شده است ----
سوال بعد:در مثلث
 که
که
 نقطه
نقطه
 روی ضلع
روی ضلع
 طوری قرار دارد که
طوری قرار دارد که
 بر
بر
 عمود است.دایره ای که از
عمود است.دایره ای که از
 میگذرد و بر
میگذرد و بر
 در
در
 مماس است،ضلع
مماس است،ضلع
 را برای دومین بار در
را برای دومین بار در
 قطع میکند.
قطع میکند.
 روی
روی
 طوری قرار دارد که
طوری قرار دارد که
 ،اگر چهار نقطه
،اگر چهار نقطه
 روی یک دایره باشند،نشان دهید
روی یک دایره باشند،نشان دهید
 بر
بر
 عمود است.
عمود است.
البته هنوز سوال آقاي پويا حل نشده است. هر كي حل كرد لطفا جوابشو بذاره. اينم سوال بعد:
فرض کنید دایره ی w به مرکز O دایره ی محیطی مثلث ABC باشد و
 . فرض کنید D محل برخورد خط AB با عمودی که در C بر ضلع AC وارد می شود باشد. خط l از نقطه ی D گذشته و بر AO عمود است. محل برخورد l و AC را E و محل برخورد l و دایره ی w را که بین E و D قرار دارد F می نامیم. ثابت کنید دایره های محیطی مثلث های BFE و CFD در نقطه ی F بر یکدیگر مماسند.
. فرض کنید D محل برخورد خط AB با عمودی که در C بر ضلع AC وارد می شود باشد. خط l از نقطه ی D گذشته و بر AO عمود است. محل برخورد l و AC را E و محل برخورد l و دایره ی w را که بین E و D قرار دارد F می نامیم. ثابت کنید دایره های محیطی مثلث های BFE و CFD در نقطه ی F بر یکدیگر مماسند.
فرض کنید دایره ی w به مرکز O دایره ی محیطی مثلث ABC باشد و
نتیجه میده دو دایره بر هم مماسند.
---- دو نوشته به هم متصل شده است ----
سوال بعد:در مثلث

















پاسخ : ماراتن هندسه
سوال بعد رو لطف میکنید؟
محل برخورد CD و AO رو T بگیرید.به وضوح T رو w میفته.حالا E مرکز ارتفاعی مثلث ATD هست و TBA هم 90 است،پس T,E,B هم خطن.پس
 که این
که این
نتیجه میده دو دایره بر هم مماسند.
---- دو نوشته به هم متصل شده است ----
سوال بعد:در مثلث
 که
که
 نقطه
نقطه
 روی ضلع
روی ضلع
 طوری قرار دارد که
طوری قرار دارد که
 بر
بر
 عمود است.دایره ای که از
عمود است.دایره ای که از
 میگذرد و بر
میگذرد و بر
 در
در
 مماس است،ضلع
مماس است،ضلع
 را برای دومین بار در
را برای دومین بار در
 قطع میکند.
قطع میکند.
 روی
روی
 طوری قرار دارد که
طوری قرار دارد که
 ،اگر چهار نقطه
،اگر چهار نقطه
 روی یک دایره باشند،نشان دهید
روی یک دایره باشند،نشان دهید
 بر
بر
 عمود است.
عمود است.
نتیجه میده دو دایره بر هم مماسند.
---- دو نوشته به هم متصل شده است ----
سوال بعد:در مثلث

















پاسخ : ماراتن هندسه
:39::7:
منظورتون این هست که سوال جدید بزارم؟یا یه چیز دیگست منظورتون؟
ادیت_1:این پستم فقط برا من این جوری شده،یا برا شما هم این جوری افتاده؟
ادیت_2:هیچی اشتباه شد d:
سوال بعد رو لطف میکنید؟
سوال بعد:در مثلث
 که
که
 نقطه
نقطه
 روی ضلع
روی ضلع
 طوری قرار دارد که
طوری قرار دارد که
 بر
بر
 عمود است.دایره ای که از
عمود است.دایره ای که از
 میگذرد و بر
میگذرد و بر
 در
در
 مماس است،ضلع
مماس است،ضلع
 را برای دومین بار در
را برای دومین بار در
 قطع میکند.
قطع میکند.
 روی
روی
 طوری قرار دارد که
طوری قرار دارد که
 ،اگر چهار نقطه
،اگر چهار نقطه
 روی یک دایره باشند،نشان دهید
روی یک دایره باشند،نشان دهید
 بر
بر
 عمود است.
عمود است.

















منظورتون این هست که سوال جدید بزارم؟یا یه چیز دیگست منظورتون؟
ادیت_1:این پستم فقط برا من این جوری شده،یا برا شما هم این جوری افتاده؟
ادیت_2:هیچی اشتباه شد d:
آخرین ویرایش توسط مدیر
پاسخ : ماراتن هندسه
ببخشید y رو که تعریف نکردین!
محل برخورد cd و ao رو t بگیرید.به وضوح t رو w میفته.حالا e مرکز ارتفاعی مثلث atd هست و tba هم 90 است،پس t,e,b هم خطن.پس
 که این
که این
نتیجه میده دو دایره بر هم مماسند.
---- دو نوشته به هم متصل شده است ----
سوال بعد:در مثلث
 که
که
 نقطه
نقطه
 روی ضلع
روی ضلع
 طوری قرار دارد که
طوری قرار دارد که
 بر
بر
 عمود است.دایره ای که از
عمود است.دایره ای که از
 میگذرد و بر
میگذرد و بر
 در
در
 مماس است،ضلع
مماس است،ضلع
 را برای دومین بار در
را برای دومین بار در
 قطع میکند.
قطع میکند.
 روی
روی
 طوری قرار دارد که
طوری قرار دارد که
 ،اگر چهار نقطه
،اگر چهار نقطه
 روی یک دایره باشند،نشان دهید
روی یک دایره باشند،نشان دهید
 بر
بر
 عمود است.
عمود است.
نتیجه میده دو دایره بر هم مماسند.
---- دو نوشته به هم متصل شده است ----
سوال بعد:در مثلث

















- ارسال ها
- 159
- لایک ها
- 282
- امتیاز
- 0
پاسخ : ماراتن هندسه

---- دو نوشته به هم متصل شده است ----
پس
 محاطي است. همچنين اگر
محاطي است. همچنين اگر
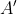 قرينه
قرينه
 نسبت به
نسبت به
 باشد بديهي است كه روي اين دايره قرار دارد. پس فرض كنيد
باشد بديهي است كه روي اين دايره قرار دارد. پس فرض كنيد
 مبدا مختصات و
مبدا مختصات و
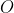 مركز اين دايره است، پس فروض مان به اينها تبديل مي شود
مركز اين دايره است، پس فروض مان به اينها تبديل مي شود

و حكم به اين تبديل مي شود كه
 چرا كه اين معادل است با اين كه
چرا كه اين معادل است با اين كه
 قطري از دايره باشد كه نتيجه مي دهد
قطري از دايره باشد كه نتيجه مي دهد
 كه همان حكم مساله است.
كه همان حكم مساله است.

پس كافيست بگوييم


حال فرض كنيد
 بنابرين كافيست بگوييم داريم
بنابرين كافيست بگوييم داريم


البته دقت كنيد


اما طبق فروض مساله
 پس
پس
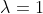 پس
پس
 كه حكم را نتيجه مي دهد.
كه حكم را نتيجه مي دهد.
پس كافيست بگوييم
حال فرض كنيد
البته دقت كنيد
اما طبق فروض مساله
---- دو نوشته به هم متصل شده است ----
سوال بعد : مماس در
 بر دايره محيطي مثلث
بر دايره محيطي مثلث
 خط
خط
 را در
را در
 قطع ميكند و پاي ارتفاع هاي راس هاي
قطع ميكند و پاي ارتفاع هاي راس هاي
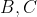 به ترتيب
به ترتيب
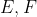 هستند. فرض كنيد
هستند. فرض كنيد
 مركز ارتفاعي باشد و
مركز ارتفاعي باشد و
 و
و
 وسط
وسط
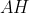 باشد.
باشد.
ثابت كنيد
 است.
است.
ثابت كنيد
آخرین ویرایش توسط مدیر
پاسخ : ماراتن هندسه

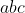




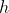


 اگر n وسط bc باشه،h مركز ارتفاعيه aqn هم هست.پس كافيه ثابت كنيم كه pm بر an عموده يا m مركز ارتفاعيه apn است.همچنين amno متوازى الاضلاعه پس ao , mn موازين.پس mn بر ap عموده.كه نتيجه ميده m مركز ارتفاعيه apn هه.
اگر n وسط bc باشه،h مركز ارتفاعيه aqn هم هست.پس كافيه ثابت كنيم كه pm بر an عموده يا m مركز ارتفاعيه apn است.همچنين amno متوازى الاضلاعه پس ao , mn موازين.پس mn بر ap عموده.كه نتيجه ميده m مركز ارتفاعيه apn هه.
---- دو نوشته به هم متصل شده است ----
سوال بعد(زياد قشنگ نيست)
سه نقطه روى اضلاع مثلثى قرار دارن به طورى كه مثلثى تشكيل ميدن كه مركز دايره محاطى داخلى آن بر مركز دايره محاطيه مثلث اصلى منطبق است.همچنين شعاع دايره محاطى داخلى آن نصف شعاع دايره محاطى داخلى مثلث اصليست.نشان دهيد هر دو مثلث متساوى الاضلاع هستند.
سوال بعد : مماس در
بر دايره محيطي مثلث
خط
را در
قطع ميكند و پاي ارتفاع هاي راس هاي
به ترتيب
هستند. فرض كنيد
مركز ارتفاعي باشد و
و
وسط
باشد.ثابت كنيد
 است.
است.
---- دو نوشته به هم متصل شده است ----
سوال بعد(زياد قشنگ نيست)
سه نقطه روى اضلاع مثلثى قرار دارن به طورى كه مثلثى تشكيل ميدن كه مركز دايره محاطى داخلى آن بر مركز دايره محاطيه مثلث اصلى منطبق است.همچنين شعاع دايره محاطى داخلى آن نصف شعاع دايره محاطى داخلى مثلث اصليست.نشان دهيد هر دو مثلث متساوى الاضلاع هستند.
- ارسال ها
- 288
- لایک ها
- 154
- امتیاز
- 43
پاسخ : ماراتن هندسه
ابتدا راس های مثلث اصلی را a و b و c می نامیم نقاط روی ab و ac و bc را به ترتیب d و e و f می نامیم همیچنین محل برخورد خط be با df را y و برخورد de با af را x و برخورد ef با cd را z و مراکز دوایر محاطی را i می نامیم. حال بریم سراغ اثبات سوال!! :
می دانیم طول مماس های مرسوم از یک نقطه بر دایره با هم برابر است. پس ad با ae برابر است . پس مثلث ade متساوی الساقین است از طرفی چون مثلث متساوی الساقین است نیمساز و عمود منصف منطبق اند پس ai عمود منصف de است. همچنین می دانیم فاصله ی هر نقطه روی عمود منصف از دو سر پاره خط به یک فاصله است پس df با fe برابر است و چون مثلث def متساوی اساقین است پس نیمساز و ارتفاع آن بر هم منطبق اند و چون ai و fi ارتفاع های مثلث های ade و def هم هستند هستند هم خط اند و در چهارضلعی adfe قطر af بر de عمود است. پس می دانیم id و ix به ترتیب شعاع های دوایر محاطی مثلث های abc و def هستند. پس id دو برابر ix است.حال در مثلث قایم الزاویه dix سینوس زاویه idx برابر 1/2 است پس این زاویه 30 درجه است. به طریق مشابه می توان ثابت کرد زاویه ی idy برابر 30 درجه است پس داریم:
Idx+idy=edf=30+30=60
به طریق مشابه می توان ثابت کرد dfe و fed برابر 60 درجه است . پس مثلث def متساوی الاضلاع است . بریم سراغ abc !!!
به کمان fd و fe برابر 120 درجه است پس جمعشون میشه 240. همچنین کمان de نیز 120 درجه است پس زاویه bac به راحتی به دست می آید که برابر 60 درجه است به همین طریق می توان ثابت کرد abc و acb نیز 60 درجه هستند پس abc نیز متساوی الاضلاع است. تموم شد!!! ببخشید نمی دونم چرا لاتکسم خرابه. سوال بعد را لطف کنید اگه پیدا کردم خودم میذارم
---- دو نوشته به هم متصل شده است ----
ببخشید حروفم کوچیک نوشت شما بزرگ در نظر بگیرید!!! :3:
ابتدا راس های مثلث اصلی را a و b و c می نامیم نقاط روی ab و ac و bc را به ترتیب d و e و f می نامیم همیچنین محل برخورد خط be با df را y و برخورد de با af را x و برخورد ef با cd را z و مراکز دوایر محاطی را i می نامیم. حال بریم سراغ اثبات سوال!! :
می دانیم طول مماس های مرسوم از یک نقطه بر دایره با هم برابر است. پس ad با ae برابر است . پس مثلث ade متساوی الساقین است از طرفی چون مثلث متساوی الساقین است نیمساز و عمود منصف منطبق اند پس ai عمود منصف de است. همچنین می دانیم فاصله ی هر نقطه روی عمود منصف از دو سر پاره خط به یک فاصله است پس df با fe برابر است و چون مثلث def متساوی اساقین است پس نیمساز و ارتفاع آن بر هم منطبق اند و چون ai و fi ارتفاع های مثلث های ade و def هم هستند هستند هم خط اند و در چهارضلعی adfe قطر af بر de عمود است. پس می دانیم id و ix به ترتیب شعاع های دوایر محاطی مثلث های abc و def هستند. پس id دو برابر ix است.حال در مثلث قایم الزاویه dix سینوس زاویه idx برابر 1/2 است پس این زاویه 30 درجه است. به طریق مشابه می توان ثابت کرد زاویه ی idy برابر 30 درجه است پس داریم:
Idx+idy=edf=30+30=60
به طریق مشابه می توان ثابت کرد dfe و fed برابر 60 درجه است . پس مثلث def متساوی الاضلاع است . بریم سراغ abc !!!
به کمان fd و fe برابر 120 درجه است پس جمعشون میشه 240. همچنین کمان de نیز 120 درجه است پس زاویه bac به راحتی به دست می آید که برابر 60 درجه است به همین طریق می توان ثابت کرد abc و acb نیز 60 درجه هستند پس abc نیز متساوی الاضلاع است. تموم شد!!! ببخشید نمی دونم چرا لاتکسم خرابه. سوال بعد را لطف کنید اگه پیدا کردم خودم میذارم
---- دو نوشته به هم متصل شده است ----
ببخشید حروفم کوچیک نوشت شما بزرگ در نظر بگیرید!!! :3:
پاسخ : ماراتن هندسه
ببخشید من اثبات شما رو متوجه نشدم! الان نقاط روی اضلاع که مرکز دایره ی محاطی مثلثشون بر مرکز دایره ی محاطی مثلث
 منطبقه
منطبقه
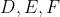 هستند؟ اگه اینجوریه چرا
هستند؟ اگه اینجوریه چرا
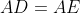 هست؟ این اتفاق فقط برای نقطه هایی که دایره ی محاطی بر اضلاع
هست؟ این اتفاق فقط برای نقطه هایی که دایره ی محاطی بر اضلاع
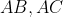 در اون نقاط مماسه رخ میده!
در اون نقاط مماسه رخ میده!
---- دو نوشته به هم متصل شده است ----
من سوال بعدو میذارم تا بتونیم ماراتن رو سریع تر پیش ببریم:
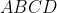 یک متوازی الاضلاع است. دایره ی با قطر
یک متوازی الاضلاع است. دایره ی با قطر
 ،
،
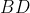 را در
را در
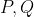 قطع می کند. عمودی که از
قطع می کند. عمودی که از
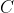 بر
بر
 رسم می شود
رسم می شود
 را به ترتیب در
را به ترتیب در
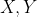 قطع می کند. ثابت کنید نقاط
قطع می کند. ثابت کنید نقاط
 روی یک دایره قرار دارند.
روی یک دایره قرار دارند.
ابتدا راس های مثلث اصلی را a و b و c می نامیم نقاط روی ab و ac و bc را به ترتیب d و e و f می نامیم همیچنین محل برخورد خط be با df را y و برخورد de با af را x و برخورد ef با cd را z و مراکز دوایر محاطی را i می نامیم. حال بریم سراغ اثبات سوال!! :
می دانیم طول مماس های مرسوم از یک نقطه بر دایره با هم برابر است. پس ad با ae برابر است . پس مثلث ade متساوی الساقین است از طرفی چون مثلث متساوی الساقین است نیمساز و عمود منصف منطبق اند پس ai عمود منصف de است. همچنین می دانیم فاصله ی هر نقطه روی عمود منصف از دو سر پاره خط به یک فاصله است پس df با fe برابر است و چون مثلث def متساوی اساقین است پس نیمساز و ارتفاع آن بر هم منطبق اند و چون ai و fi ارتفاع های مثلث های ade و def هم هستند هستند هم خط اند و در چهارضلعی adfe قطر af بر de عمود است. پس می دانیم id و ix به ترتیب شعاع های دوایر محاطی مثلث های abc و def هستند. پس id دو برابر ix است.حال در مثلث قایم الزاویه dix سینوس زاویه idx برابر 1/2 است پس این زاویه 30 درجه است. به طریق مشابه می توان ثابت کرد زاویه ی idy برابر 30 درجه است پس داریم:
Idx+idy=edf=30+30=60
به طریق مشابه می توان ثابت کرد dfe و fed برابر 60 درجه است . پس مثلث def متساوی الاضلاع است . بریم سراغ abc !!!
به کمان fd و fe برابر 120 درجه است پس جمعشون میشه 240. همچنین کمان de نیز 120 درجه است پس زاویه bac به راحتی به دست می آید که برابر 60 درجه است به همین طریق می توان ثابت کرد abc و acb نیز 60 درجه هستند پس abc نیز متساوی الاضلاع است. تموم شد!!! ببخشید نمی دونم چرا لاتکسم خرابه. سوال بعد را لطف کنید اگه پیدا کردم خودم میذارم
---- دو نوشته به هم متصل شده است ----
ببخشید حروفم کوچیک نوشت شما بزرگ در نظر بگیرید!!! :3:
می دانیم طول مماس های مرسوم از یک نقطه بر دایره با هم برابر است. پس ad با ae برابر است . پس مثلث ade متساوی الساقین است از طرفی چون مثلث متساوی الساقین است نیمساز و عمود منصف منطبق اند پس ai عمود منصف de است. همچنین می دانیم فاصله ی هر نقطه روی عمود منصف از دو سر پاره خط به یک فاصله است پس df با fe برابر است و چون مثلث def متساوی اساقین است پس نیمساز و ارتفاع آن بر هم منطبق اند و چون ai و fi ارتفاع های مثلث های ade و def هم هستند هستند هم خط اند و در چهارضلعی adfe قطر af بر de عمود است. پس می دانیم id و ix به ترتیب شعاع های دوایر محاطی مثلث های abc و def هستند. پس id دو برابر ix است.حال در مثلث قایم الزاویه dix سینوس زاویه idx برابر 1/2 است پس این زاویه 30 درجه است. به طریق مشابه می توان ثابت کرد زاویه ی idy برابر 30 درجه است پس داریم:
Idx+idy=edf=30+30=60
به طریق مشابه می توان ثابت کرد dfe و fed برابر 60 درجه است . پس مثلث def متساوی الاضلاع است . بریم سراغ abc !!!
به کمان fd و fe برابر 120 درجه است پس جمعشون میشه 240. همچنین کمان de نیز 120 درجه است پس زاویه bac به راحتی به دست می آید که برابر 60 درجه است به همین طریق می توان ثابت کرد abc و acb نیز 60 درجه هستند پس abc نیز متساوی الاضلاع است. تموم شد!!! ببخشید نمی دونم چرا لاتکسم خرابه. سوال بعد را لطف کنید اگه پیدا کردم خودم میذارم
---- دو نوشته به هم متصل شده است ----
ببخشید حروفم کوچیک نوشت شما بزرگ در نظر بگیرید!!! :3:
---- دو نوشته به هم متصل شده است ----
من سوال بعدو میذارم تا بتونیم ماراتن رو سریع تر پیش ببریم:
- ارسال ها
- 288
- لایک ها
- 154
- امتیاز
- 43
پاسخ : ماراتن هندسه
فك كنم براي سوال قبل كم توضيح دادم آقا عليرضا
چهارضلعي adfe را درنظر بگيريد. قطر af هم نيمساز a است هم نيمساز f . پس چهارضلعي adef چهارضلعي كايت است. پس با توجه به خصوصيات چهارضلعي كايت ad=ae و از همين مي توان استفاده كرد و بيان كرد كه دايره ي محاطي abc از سه راس مثلث داخلي مي گذرد. اگه خواستيد درباره ي چهارضلعي كايت بيشتر توضيح ميدم. مثلا لوزي يك نوع خاص از چهارضلعي كايت است. :37:
---- دو نوشته به هم متصل شده است ----
واي اعصابم داره خرد ميشه نمي دونم چرا با حروف كوچيك مي نويسه شما بازم بزرگ در نظر بگيريد
فك كنم براي سوال قبل كم توضيح دادم آقا عليرضا
چهارضلعي adfe را درنظر بگيريد. قطر af هم نيمساز a است هم نيمساز f . پس چهارضلعي adef چهارضلعي كايت است. پس با توجه به خصوصيات چهارضلعي كايت ad=ae و از همين مي توان استفاده كرد و بيان كرد كه دايره ي محاطي abc از سه راس مثلث داخلي مي گذرد. اگه خواستيد درباره ي چهارضلعي كايت بيشتر توضيح ميدم. مثلا لوزي يك نوع خاص از چهارضلعي كايت است. :37:
---- دو نوشته به هم متصل شده است ----
واي اعصابم داره خرد ميشه نمي دونم چرا با حروف كوچيك مي نويسه شما بازم بزرگ در نظر بگيريد
