معادله تابع (بسیار زیبا)
- شروع کننده موضوع amir.ekhlasi
- تاریخ شروع
- برچسپ ها irysc.com استفاده اعداد اعداد اول اعداد حقیقی اعداد صحیح اعداد طبیعی تابع تعریف حقیقی دنباله راهنمایی سوال عدد اول عدد صحیح مثبت مرحله دوم معادله نکته
- ارسال ها
- 327
- لایک ها
- 378
- امتیاز
- 0
پاسخ : معادله تابع (بسیار زیبا)
من تا یه جاهایی پیش رفتم.نمیدونم بدرد میخوره یا نه.دیگه خسته شدم وا دادم بقیه راهو :-؟؟(البته یه پاسخ بدیهیش
= |m|)
هست که به وضوح تو همه شرایط مساله صدق می کنه!)
=f(m).f(n)=f(-m).f(-n)\Rightarrow \frac{f(m)}{f(-m)}=\frac{f(n)}{f(-n)}=c,c\in \mathbb{R}^{+}\Rightarrow f(m)=c.f(-m)\Rightarrow f(mn)=f(m).f(n)=f(-m).f(-n)\Rightarrow c^{2}=1\: \:)
=f(-m))
=f(m).f(0)\: \: ,\: \: f(m)\not\equiv 0\Rightarrow f(0)=0)
=f(m).f(1)\Rightarrow f(1)=f(-1)=1)
\leq f(m-1)+f(1)=f(m-1)+1\leq ...\leq m)
,
:
=f(p_{1}^{\alpha _{1}}...p_{k}^{\alpha _{k}})=(f(p_{1}))^{\alpha _{1}}...(f(p_{k}))^{\alpha _{k}})
حال ثابت می کنیم که ضابطه تابع به شکل روبروست:
:f(m)=\prod_{i=1}^{k}q_{i}^{\alpha _{i}})
حال ثابت می کنیم که اگر
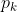نشان دهنده k امین عدد اول باشد آنگاه دنباله
صعودی است!
نمیدونم چقد درسته!؟ ولی فک کنم یذره جلو تر اگه بریم،به این نتیجه میشه رسید که .
.
لطفا مشکلای راهمو بگین... مرسی
من تا یه جاهایی پیش رفتم.نمیدونم بدرد میخوره یا نه.دیگه خسته شدم وا دادم بقیه راهو :-؟؟(البته یه پاسخ بدیهیش
پس کافی است ضابطه تابع را به ازای
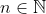بدست آوریم.
حال ثابت می کنیم که ضابطه تابع به شکل روبروست:
حال ثابت می کنیم که اگر
نمیدونم چقد درسته!؟ ولی فک کنم یذره جلو تر اگه بریم،به این نتیجه میشه رسید که .
لطفا مشکلای راهمو بگین... مرسی
آخرین ویرایش توسط مدیر
- ارسال ها
- 364
- لایک ها
- 183
- امتیاز
- 0
پاسخ : معادله تابع (بسیار زیبا)
مسئله دو حالت داره:
حالت 1: یک n ای وجود داره که f(n)>1. در این حالت کوچکترین عددی را در نظر بگیرید که این اتفاق براش میفته و ادامه بدید...
حالت 2: برعکس حالت اول. در اینصورت میشه لینک http://www.irysc.com/forum/t5245/ که اون راحتتر حل میشه...
مسئله دو حالت داره:
حالت 1: یک n ای وجود داره که f(n)>1. در این حالت کوچکترین عددی را در نظر بگیرید که این اتفاق براش میفته و ادامه بدید...
حالت 2: برعکس حالت اول. در اینصورت میشه لینک http://www.irysc.com/forum/t5245/ که اون راحتتر حل میشه...
آخرین ویرایش توسط مدیر
- ارسال ها
- 364
- لایک ها
- 183
- امتیاز
- 0
پاسخ : معادله تابع (بسیار زیبا)
حل میشه. یکذره ایده میخواد. اول حالت دوم را که ساده تره بررسی کن. اگر حالت دوم را سؤال بدند که میشه همون http://www.irysc.com/forum/t5245/ ایده دار و خلاقانه است و میتونه سؤال 3 مرحله 2 باشه. چون ایدشو احتمالا قبلا ندیدی. ولی خوب حالت اول سختتره.
حل میشه. یکذره ایده میخواد. اول حالت دوم را که ساده تره بررسی کن. اگر حالت دوم را سؤال بدند که میشه همون http://www.irysc.com/forum/t5245/ ایده دار و خلاقانه است و میتونه سؤال 3 مرحله 2 باشه. چون ایدشو احتمالا قبلا ندیدی. ولی خوب حالت اول سختتره.
- ارسال ها
- 327
- لایک ها
- 378
- امتیاز
- 0
- ارسال ها
- 364
- لایک ها
- 183
- امتیاز
- 0
پاسخ : معادله تابع (بسیار زیبا)
اون لینک pdf مشکل داره نمیتونم دانلودش کنم. اگر میشه درستش کنید تا راه حل را چک کنم. جوابتون هم فکر نکنم درست باشه. چون قانون نامساوی را برای اعداد منفی مشکل داره مثلا:
=|x|^{-1},x=2,y=-1\Rightarrow&space;f(x+y)>&space;f(x)+f(y))
راهنمایی: ضابطه جوابها در قسمت دوم یکم دور از انتظارند و کاملا به خواص نظریه اعدادی اعداد صحیح مربوطند. پس نظریه اعدادی روی قسمت دوم فکر کنید.
از شما دوست گرامی ممنونم که ایده هایتان را اینجا مطرح میکنید...
اون لینک pdf مشکل داره نمیتونم دانلودش کنم. اگر میشه درستش کنید تا راه حل را چک کنم. جوابتون هم فکر نکنم درست باشه. چون قانون نامساوی را برای اعداد منفی مشکل داره مثلا:
از شما دوست گرامی ممنونم که ایده هایتان را اینجا مطرح میکنید...
آخرین ویرایش توسط مدیر
- ارسال ها
- 327
- لایک ها
- 378
- امتیاز
- 0
پاسخ : معادله تابع (بسیار زیبا)
مثال نقضتون،نقض نمیکنه چون:
\leq f(x)+f(y)\Leftrightarrow f(1)\leq f(1)+f(2)\Leftrightarrow 0\leq f(2)=\frac{1}{2})
البته اینو که گفتین یه سوتی دیگه ام پیدا شد!ضابطه تابع من باید این باشه:
=\left\{\begin{matrix} 0 & ;x=0\ \\ |x|^c & ;x\neq 0\end{matrix}\right.)
\equiv 1)
اینم لینک جوابش:
http://up98.org/upload/server1/01/z/6h0lcjjntqt6lnp295l.pdf
فقط باید قسمت جوابای دقیق رو بدست بیارم که حتما میکنم.و ممنون از اینکه سوالاتون رو اینجا میذارین
مثال نقضتون،نقض نمیکنه چون:
البته اینو که گفتین یه سوتی دیگه ام پیدا شد!ضابطه تابع من باید این باشه:
که در آن
)
است.(سوتی این بود که
غیر قابل قبوله)
یه جواب دیگه هم اینه:
یه جواب دیگه هم اینه:
اینم لینک جوابش:
http://up98.org/upload/server1/01/z/6h0lcjjntqt6lnp295l.pdf
فقط باید قسمت جوابای دقیق رو بدست بیارم که حتما میکنم.و ممنون از اینکه سوالاتون رو اینجا میذارین
آخرین ویرایش توسط مدیر
- ارسال ها
- 364
- لایک ها
- 183
- امتیاز
- 0
پاسخ : معادله تابع (بسیار زیبا)
توی راه حلتون یه جوب هست که باعث شده به اشتباه بیفتید. اونجا که میخواستید تابع را به کوشی جمعی تبدیل کنید، به این نکته دقت نکردید که هر عدد صحیح را نمیتوان به صورت دو بتوان x نوشت. اون برای اعداد حقیقی بود که میتونستیم اینکار را بکنیم به طوری که دامنه تعریف تغییر نکند! یعنی شما f را فقط برای اعداد صحیح به صورت دو بتوان x پیدا کردید.
توی راه حلتون یه جوب هست که باعث شده به اشتباه بیفتید. اونجا که میخواستید تابع را به کوشی جمعی تبدیل کنید، به این نکته دقت نکردید که هر عدد صحیح را نمیتوان به صورت دو بتوان x نوشت. اون برای اعداد حقیقی بود که میتونستیم اینکار را بکنیم به طوری که دامنه تعریف تغییر نکند! یعنی شما f را فقط برای اعداد صحیح به صورت دو بتوان x پیدا کردید.
- ارسال ها
- 364
- لایک ها
- 183
- امتیاز
- 0
پاسخ : معادله تابع (بسیار زیبا)
چون مدتی گذشتو کسی جواب نذاشت، جوابشو میذارم.
جوابهای بدیهی آن f=1 و f=0 است. غیر از اینها بدیهی است که
=0,f(1)=1,f(-n)=f(n))
و
\leqslant&space;n)
. از این به بعد منظورم از n عدد صحیح مثبت است. به دو حالت میرسیم:
حالت 1:
\leqslant&space;1)
حالت 2:
>&space;1)
ابتدا حالت 1 را بررسی میکنیم:
اگر
=1)
در این صورت طبق بزو اعداد صحیح
وجود دارند که
. اما در اینصورت از آنجا که
,f(b)\leqslant&space;1)
داریم:
=f(am+bn)\leqslant&space;f(a)f(m)+f(b)f(n)\leqslant&space;f(m)+f(n))
یعنی
+f(n)\geqslant&space;1)
. اما اگر
,f(n))
هر دو اکیدا کمتر از یک باشند، در اینصورت اعداد طبیعی بزرگ
وجود داردند که
^M,f(n)^N<0.5)
. اما از آنجا که
=1)
پس
+f(n^N)<\frac{1}{2}+\frac{1}{2}\leqslant&space;1)
که یک تناقض است. یعنی به ازای هر دو عدد m,n که نسبت به هم اولند، یکی از مقادیر
)
یا
)
برابر 1 است. درواقع حداکثر یک عدد اول مانند p وجود دارد که
<1)
. پس تابع f به شکل
=\beta&space;^{\left&space;\|&space;n&space;\right&space;\|_p})
است که در آن p یک عدد اول و بتا عددی حقیقی بین صفر و یک است. به راحتی میشه دید که هر تابع به این شکل هم در شرایط مسئله صدق میکند.
حالت 2: فرض کنید p کوچکترین عدد طبیعی باشد که
>1)
. واضح است که p اول است ولی مهم نیست. همچنین عدد حقیقی آلفا وجود دارد که
و
=p^\alpha)
. در این صورت هر عدد طبیعی n را که
میتوان به طور یکتا در مبنای p به شکل زیر نوشت:
در اینصورت چون p کوچکترین عدد انتخاب شده است، پس
\leqslant&space;1)
، پس داریم
=f(a_0+a_1p+...a_sp^s)\leqslant&space;f(1)+f(p)+...+f(p^s)=1+p^\alpha+...+p^{s\alpha}=p^{s\alpha}(1+p^{-\alpha}+...+p^{-s\alpha})\leqslant&space;n^\alpha&space;\sum_{k=0}^\infty&space;{p^{-k\alpha}}=n^\alpha&space;C)
که در آن C یک عدد ثابت و مستقل از n است. پس اگر در نامساوی بالا به جای n بذاریم
خواهیم داشت:
\leqslant&space;n^{N\alpha}C\Rightarrow&space;f(n)\leqslant&space;n^\alpha\sqrt[N]{C})
با
نتیجه میشه که
\leqslant&space;n^\alpha)
.
از طرفی با استفاده از نامساویی که به دست آوردیم و نامساویی که جزو شرط مسئله بود و اینکه
داریم:
\geqslant&space;f(p^{s+1})-f(p^{s+1}-n)\geqslant&space;p^{(s+1)\alpha}-(p^{s+1}-n)^\alpha\geqslant&space;\\p^{(s+1)\alpha}-(p^{s+1}-p^s)^\alpha=p^{(s+1)\alpha}[1-(1-\frac{1}{p})^\alpha]\geqslant&space;C'n^\alpha)
که در آن 'C یک عدد ثابت و مستقل از n است. پس میتونیم مثل بالا عمل کنیم و به جای n،
بذاریم و با
به این نتیجه برسیم که
\geqslant&space;n^\alpha)
و در نتیجه
=n^\alpha)
. پس در این حالت نیز تابع به شکل
=|n|^\alpha)
که در آن
است. و همچنین میتوان دید هر تابع به این شکل در شرایط مسئله صدق میکند.
چون مدتی گذشتو کسی جواب نذاشت، جوابشو میذارم.
جوابهای بدیهی آن f=1 و f=0 است. غیر از اینها بدیهی است که
حالت 1:
حالت 2:
ابتدا حالت 1 را بررسی میکنیم:
اگر
یعنی
حالت 2: فرض کنید p کوچکترین عدد طبیعی باشد که
از طرفی با استفاده از نامساویی که به دست آوردیم و نامساویی که جزو شرط مسئله بود و اینکه
آخرین ویرایش توسط مدیر