هندسه صفر تا 100
bgo گفت
از نقطه A محل تماس دو دایره مساوی و مماس بر هم خطی رسم میکنیم تا آن ها را دوباره در B,C قطع کند سپس از نقطه C بر BC خطی عمود رسم می کنیم و از نقطه B خطی موازی خط المرکزین رسم می کنیم تا یکدیگر را در M قطع کنند. اگر قاطع BAC حول نقطه A دوران کند مکان هندسی M را بیابید
یکی میشه یه سوال (امتحان هندسه ۲ نباشه مثله این


in soalo mmath va bgo ghablan didan, vali shoma ke nadidin halesh konin, asune
tu ABC, dayere mohati be BC,CA va AB tu D,E va F momase. ye dayere az B va C rad mishe va be dayere mohati tu X momase. Y va Z ro ham haminjuri tarif konin. sabet konin dayere mohiti haye IDX,IEY va IFZ tu ye noghte begheire I hamresan. I hamun markaze dayere mohatiye
fereidoon گفت
راه حل ساده نداره؟(اخه من داشتم با محاطی بازی و یه خرده از خواص مثلث استفاده می کردم و به نتایج خوبی رسیدم)
PS: یه نگاه به اون دو تا سوالی که گفتم بندازید. خیلی شبیه به این سوال هستند.
Aref گفت
fereidoon گفت
راه حل ساده نداره؟(اخه من داشتم با محاطی بازی و یه خرده از خواص مثلث استفاده می کردم و به نتایج خوبی رسیدم)
PS: یه نگاه به اون دو تا سوالی که گفتم بندازید. خیلی شبیه به این سوال هستند.
زحمت سوال بد هم اگه بکشی , ممنون میشیم اجماعا

کافیه که ثابت کنیم مراکز سه تا دایره ی گفته شده هم خط اند. چون همشون از I میگذرند و اگه این هم خطی ثابت بشه محل برخورد دوم دو تا از دایره هارو میگیریم و واضحه که مرکز دایره ی سوم از اون نقطه و I به یک فاصله است.
 رو به ترتیب عمود منصف های پاره خط های
رو به ترتیب عمود منصف های پاره خط های
 می گیریم. باید ثابت کنیم مثلثی که از محل برخورد خطوط
می گیریم. باید ثابت کنیم مثلثی که از محل برخورد خطوط
 به وجود میاد با مثلثی که از محل برخورد خطوط
به وجود میاد با مثلثی که از محل برخورد خطوط
 به وجود میاد همسان هستند. حالا اون مثلث هارو
به وجود میاد همسان هستند. حالا اون مثلث هارو
 و
و
 میگیریم.
میگیریم.
۱. مشکل این قسمت هنوز برطرف نشده
 ، چون این لم با این صورت غلطه و احتمالا چیز دیگه بوده.
، چون این لم با این صورت غلطه و احتمالا چیز دیگه بوده.
۲. کم لطفی نکنید
 ! سعی کنید سطح سوال هایی که میذارید در حد ماراتن باشه نه امتحان نهایی .
! سعی کنید سطح سوال هایی که میذارید در حد ماراتن باشه نه امتحان نهایی .

Aref گفت
حالا از این لم استفاده می کنیم: اگر
 دو دایره باشند که در دو نقطه ی
دو دایره باشند که در دو نقطه ی
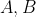 متقاطع باشند و هر دوی آن ها بر دایره به مرکز
متقاطع باشند و هر دوی آن ها بر دایره به مرکز
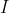 در نقاط
در نقاط
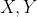 مماس داخل باشند آنگاه محل بر خورد عمود منصف های دو پاره خط
مماس داخل باشند آنگاه محل بر خورد عمود منصف های دو پاره خط
 روی پاره خط
روی پاره خط
 قرار دارد. پس دو مثلث
قرار دارد. پس دو مثلث
 همسانند و مساله حل شد.
همسانند و مساله حل شد.

kamymath گفت
ABCD is a square. E is a point of [AB]. P is the intersection point of [DE] and the diagonal [AC].
Through P , draw a line L that is perpendicular to [DE]
F is the intersection point of L and [BC]
PROVE :
EA + FC = EF
Through P , draw a line L that is perpendicular to [DE]
F is the intersection point of L and [BC]
PROVE :
EA + FC = EF



