هندسه صفر تا 100
Let AH_1, BH_2 , and CH_3 be the altitudes of an acute scalene triangle ABC
The incircle of triangle ABC is tangent to BC,CA, and AB at T_1,T_2, and T_3, respectively
For i =1, 2, 3 let P_i be the point on line H_i H_i+1 (where H_4 = H_1) such that H_i T_i P_i is an acute isosceles triangle with H_i T_i = H_i P_i
Prove that the circumcircles of triangles T_i P_i T_i+1 for i=1,2,3 pass through a common point
mahdisaj گفت
اگر موافق باشید بریمسوال بعد :
اگر O محل برخورد اقطار 4 ضلعی ABCD باشد و
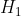 مرکز ارتفاعی مثلث AOD و
مرکز ارتفاعی مثلث AOD و
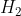 مرکز ارتفاعی مثلث BOC باشد و
مرکز ارتفاعی مثلث BOC باشد و
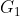 مرکز ثقل مثلث DOC و
مرکز ثقل مثلث DOC و
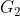 مرکز ثقل مثلث AOB باشد ثابت کنید :
مرکز ثقل مثلث AOB باشد ثابت کنید :

اگر O محل برخورد اقطار 4 ضلعی ABCD باشد و
پس کافیست ثابت کنیم H_1 H_2 عمود به MN
.
حالا دایره های به قطر AB , CD رو در نظر بگیرید ، M,N مرکز این ۲تا هستند ،, H_2 , H_1 هم رو یه محور اصلی این دو دایره هستند چون
ADEF,BCZT محاطی هستند .
پس H_1 H_2 محور اصلیه پس خط المرکزین MN بهش عموده !
تمام !!!!

mmath گفت
Let AH_1, BH_2 , and CH_3 be the altitudes of an acute scalene triangle ABC
The incircle of triangle ABC is tangent to BC,CA, and AB at T_1,T_2, and T_3, respectively
For i =1, 2, 3 let P_i be the point on line H_i H_i+1 (where H_4 = H_1) such that H_i T_i P_i is an acute isosceles triangle with H_i T_i = H_i P_i
Prove that the circumcircles of triangles T_i P_i T_i+1 for i=1,2,3 pass through a common point
پاسخ : هندسه صفر تا 100
مثلثabc مفروض است.ارتفاع هاي a,b,c به ترتيب d,e,f نامگذاري شده است,ثابت كنيد:
1)خط هاي اويلري مثلث هاي aef,bed,cdf در نقطه اي مانند k همرسند
2)در بين kd,ke,kf بزرگترينشان برابر جمع دوتاي ديگر است
اين سوال معروفيه,ولي به هر حال براي اين كه اين تاپيك دوباره راه بيفته,نوشتم!:63:
مثلثabc مفروض است.ارتفاع هاي a,b,c به ترتيب d,e,f نامگذاري شده است,ثابت كنيد:
1)خط هاي اويلري مثلث هاي aef,bed,cdf در نقطه اي مانند k همرسند
2)در بين kd,ke,kf بزرگترينشان برابر جمع دوتاي ديگر است
اين سوال معروفيه,ولي به هر حال براي اين كه اين تاپيك دوباره راه بيفته,نوشتم!:63:
پاسخ : هندسه صفر تا 100
خیلی سخت نیست سوالش ،ولی باید وقت بذاری روش چون شلوغه شکلش .
اون سوال هم حل کرده بودیم قبلا ، فک می کنم تو تمرین های انتهای کتاب آقای احمد پور هم هست .
یه سوال ساده تر میزارم فعلا ، شاید راه افتاد ماراتن !

D,L که معلومه چین. AI دایره ADL رو در J قطع میکنه ، DM موازی AJ هست .W_1 رو دایره نه نقطه DML در نظر بگیرید .
اگه دایره های W_2 , W_3 هم اینجوری تعریف بشن ثابت کنید W_1 , W_2, W_3 هم محورن .
(توی این شکل یه راهنمایی هم هست البته :95
چرا فك كردم,خيلي خفن بود,سرم گيج رفت!!!:188:
اون سوال قبلي كه گذاشتمو حل كرده بوديد؟
اون سوال قبلي كه گذاشتمو حل كرده بوديد؟
اون سوال هم حل کرده بودیم قبلا ، فک می کنم تو تمرین های انتهای کتاب آقای احمد پور هم هست .
یه سوال ساده تر میزارم فعلا ، شاید راه افتاد ماراتن !
D,L که معلومه چین. AI دایره ADL رو در J قطع میکنه ، DM موازی AJ هست .W_1 رو دایره نه نقطه DML در نظر بگیرید .
اگه دایره های W_2 , W_3 هم اینجوری تعریف بشن ثابت کنید W_1 , W_2, W_3 هم محورن .
(توی این شکل یه راهنمایی هم هست البته :95
آخرین ویرایش توسط مدیر
پاسخ : هندسه صفر تا 100
http://www.artofproblemsolving.com/Forum/download/file.php?id=24908&mode=view
درست شد برادر ؟
اگه بازم مشکلی* هست بفرما .
من شكلي نميبينم!اگه كسي ميبينه,يه لينكي بيداره لطفا!
اون مسئله هم(ته كتاب احمدپور)يه زماني open بوده-تا يه قرن پيش فك كنم-,به نظرم راحت نبود ولي خب ...
اون مسئله هم(ته كتاب احمدپور)يه زماني open بوده-تا يه قرن پيش فك كنم-,به نظرم راحت نبود ولي خب ...
http://www.artofproblemsolving.com/Forum/download/file.php?id=24908&mode=view
درست شد برادر ؟
اگه بازم مشکلی* هست بفرما .
پاسخ : هندسه صفر تا 100
Let D be a point on the side BC of a triangle ABC. Let O, X and Y be the circumcenters of triangles ABC, ABD and ACD.
Let M be the midpoint of the side BC of triangle ABC. Prove that the perpendicular bisector of the segment AM passes through the midpoint of the segment XY.
Let M be the midpoint of the side BC of triangle ABC. Prove that the perpendicular bisector of the segment AM passes through the midpoint of the segment XY.
پاسخ : هندسه صفر تا 100
فرض کن k,l نقاطی باشند که روی x, y هستند و k,l,d همخطند و kl بر ad عمود باشه. اگر f وسط kl باشه اونوقت به دلیل تشابه akl و abc داریم زاویه ی afd + amd=180 و از طرفی داریم adf=90 پس amf=90 و در نتیجه چون وسط af وسط xy هست حله.
در مثلث abc ، داریم d پای نیمساز داخلی a و 2_i,i_1,i به ترتیب مرکز دایره ی محاطی داخلی abc , adb,adc هست.اگر x روی عمودمنصف i_1i_2 باشه و i_1xi_2 = a/2 باشه ثابت کن که xd بر bc عموده.x هم همطرف d نسبت به i_1i_2 انتخاب می شه.
فرض کن k,l نقاطی باشند که روی x, y هستند و k,l,d همخطند و kl بر ad عمود باشه. اگر f وسط kl باشه اونوقت به دلیل تشابه akl و abc داریم زاویه ی afd + amd=180 و از طرفی داریم adf=90 پس amf=90 و در نتیجه چون وسط af وسط xy هست حله.
در مثلث abc ، داریم d پای نیمساز داخلی a و 2_i,i_1,i به ترتیب مرکز دایره ی محاطی داخلی abc , adb,adc هست.اگر x روی عمودمنصف i_1i_2 باشه و i_1xi_2 = a/2 باشه ثابت کن که xd بر bc عموده.x هم همطرف d نسبت به i_1i_2 انتخاب می شه.
- ارسال ها
- 32
- لایک ها
- 8
- امتیاز
- 0
پاسخ : هندسه صفر تا 100
این سؤالو تا اون جا که من می دونم پاسخ داده بشه همه ی تاپیکا که فریدون دوست داره جلو می رن. راه حل این سؤالو یادم نمی اومد. دوباره فک کردم باقیشو خودتون برین دیگه. امیدوارم اشتباه نگم:
این عمود منصفه یه نقطه ای نیمسازو قطع می کنه. این نقطه رو بذارید p. نقطه ی m هم وسط i_1,i_2 حالا با توجه به این که i_1m^2=mp.mx داریم md^2=mp.mx حالا زاویه ی mdx مساوی mpd است کافیست mdb رو ازش جداگونه بپرونید. اگه اشتباه نکنم این جاشو با دیدن اون چهارضلعی معروفه (پای عمود از I به روی bc و d و i_1 و i_2) بررسی کردم و باقیشم باید زاویه بازی بشه.)
سه تا دایره ی هم مرکز با شعاع های مفروض دادن. مثلث با بیشترین مساحت که رؤوسش روی این دایره ها برن رو پیدا کنید. اینو همین الان که داشتم می نوشتم به ذهنم رسید که بگم در شرایط کلی هم مسأله رو حل کنید(دایره ها همگی هم مرکز نباشند). تضمینی نیس که جواب آدم ایزادی داشته باشه ها.
توجه کنید یه جوب خیلی رایج در حل مسایل فوق اینه که شما بیاید بگید مثلا بزرگترین مثلثو می گیریم و بعد این جوریه و.... جمله ی وجود مثلث مینیمال هنوز ثابت نشده است و با توجه به فضای پیوسته ای که هندسه دارد ممکن است شکلی حدی داشته باشیم (مثل گفتن نزدیک ترین عدد در بازه ی [2,3) به 1 چیه؛ مث نامساوی هایی که از تساوی تبعیت نمی کنند.) ما از این کارا تو فضای گسسته زارت و زورت انجام می دیم (البته بعضی جا ها هم مث گراف اینا یه کم دیده می شن(بحثای اکسترمم، ماکسیمم و ماکسیمال،...)). ولی این جا این طوری نیست. خلاصه این بحثا کار داره. همین جوری هم الکی نمی شه استفاده ی این جوری کرد.
:231:
این سؤالو تا اون جا که من می دونم پاسخ داده بشه همه ی تاپیکا که فریدون دوست داره جلو می رن. راه حل این سؤالو یادم نمی اومد. دوباره فک کردم باقیشو خودتون برین دیگه. امیدوارم اشتباه نگم:
این عمود منصفه یه نقطه ای نیمسازو قطع می کنه. این نقطه رو بذارید p. نقطه ی m هم وسط i_1,i_2 حالا با توجه به این که i_1m^2=mp.mx داریم md^2=mp.mx حالا زاویه ی mdx مساوی mpd است کافیست mdb رو ازش جداگونه بپرونید. اگه اشتباه نکنم این جاشو با دیدن اون چهارضلعی معروفه (پای عمود از I به روی bc و d و i_1 و i_2) بررسی کردم و باقیشم باید زاویه بازی بشه.)
سه تا دایره ی هم مرکز با شعاع های مفروض دادن. مثلث با بیشترین مساحت که رؤوسش روی این دایره ها برن رو پیدا کنید. اینو همین الان که داشتم می نوشتم به ذهنم رسید که بگم در شرایط کلی هم مسأله رو حل کنید(دایره ها همگی هم مرکز نباشند). تضمینی نیس که جواب آدم ایزادی داشته باشه ها.
توجه کنید یه جوب خیلی رایج در حل مسایل فوق اینه که شما بیاید بگید مثلا بزرگترین مثلثو می گیریم و بعد این جوریه و.... جمله ی وجود مثلث مینیمال هنوز ثابت نشده است و با توجه به فضای پیوسته ای که هندسه دارد ممکن است شکلی حدی داشته باشیم (مثل گفتن نزدیک ترین عدد در بازه ی [2,3) به 1 چیه؛ مث نامساوی هایی که از تساوی تبعیت نمی کنند.) ما از این کارا تو فضای گسسته زارت و زورت انجام می دیم (البته بعضی جا ها هم مث گراف اینا یه کم دیده می شن(بحثای اکسترمم، ماکسیمم و ماکسیمال،...)). ولی این جا این طوری نیست. خلاصه این بحثا کار داره. همین جوری هم الکی نمی شه استفاده ی این جوری کرد.
:231:
آخرین ویرایش توسط مدیر
پاسخ : هندسه صفر تا 100
من نفهميدم منظور اين گل پسر چيه.هركي فهميد به منم بگه!
اما من نمي دونم اين سوال چه جيز سختي داره كه اين تاپيك از صفحه محو شده،ماشاالله اسانيد بزرگ سايت هم هندسه شون خفه،شايد اينقدر ساده بوده كه نخواستن بنويسن.خب،خود astronomer1 راهنمايي رو گذاشته توي توضيح سوال،واقعا فقط كافيه يه مثلث رو با توجه به همون اكسترمم ها بسازيد بعد ادعا كنيم كه max هست و مسئله حل شه.هيچ چيز اضافه هم نيست.
حالا خيلي مهم نيست،مهم سوال بعديه كه مي خوام بيشتر حال و هواي مرحله سه داشته باشه:
دو دايره w[SUB]1 [/SUB]وw[SUB]2[/SUB] در نقاط A,B متقاطع اند.نقاط C و D را چنان به ترتيب روي كمان AB محصور بين w[SUB]1 [/SUB]وw[SUB]2[/SUB] انتخاب مي كنيم كه وتر مشتركCD,AB را نصف كند.خط مماس بر w[SUB]2[/SUB] از D دايره ديگر را در E,F قطع ميكند و به طور مشابه خط مماس ديگري دايره ديگرش را در X,Y قطع مي كند.ثابت كنيد FYموازيEX است.
مگه الافیم . هندسه خوشخوان فصل 1و2 را بخوانید .
اما من نمي دونم اين سوال چه جيز سختي داره كه اين تاپيك از صفحه محو شده،ماشاالله اسانيد بزرگ سايت هم هندسه شون خفه،شايد اينقدر ساده بوده كه نخواستن بنويسن.خب،خود astronomer1 راهنمايي رو گذاشته توي توضيح سوال،واقعا فقط كافيه يه مثلث رو با توجه به همون اكسترمم ها بسازيد بعد ادعا كنيم كه max هست و مسئله حل شه.هيچ چيز اضافه هم نيست.
حالا خيلي مهم نيست،مهم سوال بعديه كه مي خوام بيشتر حال و هواي مرحله سه داشته باشه:
دو دايره w[SUB]1 [/SUB]وw[SUB]2[/SUB] در نقاط A,B متقاطع اند.نقاط C و D را چنان به ترتيب روي كمان AB محصور بين w[SUB]1 [/SUB]وw[SUB]2[/SUB] انتخاب مي كنيم كه وتر مشتركCD,AB را نصف كند.خط مماس بر w[SUB]2[/SUB] از D دايره ديگر را در E,F قطع ميكند و به طور مشابه خط مماس ديگري دايره ديگرش را در X,Y قطع مي كند.ثابت كنيد FYموازيEX است.
پاسخ : هندسه صفر تا 100
XYو EF نقطه ی برخوردشون رو بذار S . حالا داریم : CX=x,SX=y,CY=z,SE=m,ED=l,DF=t
حکم با این هم ارز می شه که اگه x,y,z,m,l,t اعداد مثبتی باشند به گونه ای که

اونوقت ثابت کنیم که (x/(x+y+z)=m/(m+l+t .
که خوب با توجه به دو تا برابری اول باید ثابت بشه که :
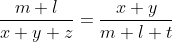
که خوب بعد از ساده شدن تبدیل می شه به این که
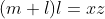 یا این که
یا این که
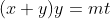 حالا اگه فرض خلف بریم میشه مثلا
حالا اگه فرض خلف بریم میشه مثلا
 که با ضرب این دو رابطه به
که با ضرب این دو رابطه به
 که با توجه به رابطه ی یک
که با توجه به رابطه ی یک
 . تناقض.
. تناقض.
پس مسئله حله ...
XYو EF نقطه ی برخوردشون رو بذار S . حالا داریم : CX=x,SX=y,CY=z,SE=m,ED=l,DF=t
حکم با این هم ارز می شه که اگه x,y,z,m,l,t اعداد مثبتی باشند به گونه ای که
اونوقت ثابت کنیم که (x/(x+y+z)=m/(m+l+t .
که خوب با توجه به دو تا برابری اول باید ثابت بشه که :
که خوب بعد از ساده شدن تبدیل می شه به این که
پس مسئله حله ...


