uvw

Dadgarnia · 1393/9/12

امشب يه چيزي به ذهنم رسيد گفتم بيام اينجا هم بنويسم ببينم درسته يا نه.
قرار ميديم

$\sum_{cyc}a=3u,\sum_{cyc}ab=3v^2,abc=w^3$

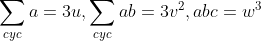مي خوام ثابت كنم هر نامساوي متقارن كه جمله هاش داراي توان صحيح هستن رو ميشه به شكل

$u,v,w$

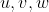بيان كرد. واضحه كه ميشه اين نامساوي رو به صورت خطي نوشت. ابتدا جمله هاي به شكل

$\sum_{cyc}a^n$

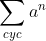رو بررسي مي كنيم. با استقرا اين كارو انجام ميديم پايه هاي استقرا

$n=1,2,3$

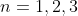هستن كه به راحتي ثابت ميشه كه حكم براشون برقراره حالا فرض مي كنيم حكم براي تمام اعداد كوچكتر از

$n+1$

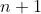درست باشه مي خوايم حكم رو به ازاي

$n+1$

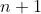ثابت كنيم. داريم:

$\sum_{cyc}a^{n+1}=\left ( \sum_{cyc}a \right )\left ( \sum_{cyc}a^n \right )-\left ( \sum_{cyc}ab \right )\left ( \sum_{cyc}a^{n-1} \right )+abc\sum_{cyc}a^{n-2}$

با توجه به فرض استقرا گام استقرا ثابت ميشه. حالا عبارات به شكل

$\sum_{cyc}a^nb^n$

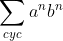رو بررسي مي كنيم. مثل قبل پايه هاي استقرا رو

$n=1,2,3$

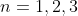قرار ميديم كه به راحتي قابل اثباتند. حالا فرض مي كنيم حكم براي تمام اعداد كوچكتر از

$n+1$

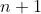درست باشه. حالا حكم رو به ازاي

$n+1$

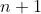ثابت مي كنيم. داريم:

$\sum_{cyc}a^{n+1}b^{n+1}=\left ( \sum_{cyc}a^nb^n \right )\left ( \sum_{cyc}ab \right )-abc\left ( \sum_{cyc}a \right )\left ( \sum_{cyc}a^{n-1}b^{n-1} \right )+$

$+a^2b^2c^2\sum_{cyc}a^{n-2}b^{n-2}$

پس گام استقرا ثابت ميشه. حالا عبارات به شكل

$\sum_{cyc}(a^mb^n+a^nb^m),m> n$

رو بررسي مي كنيم دقت كنيد كه عبارات به شكل

$\sum_{cyc}(a^mb^nc^p+a^mb^pc^n),m\geq n\geq p$

رو مي توان به شكل

$a^pb^pc^p\sum_{cyc}(a^{m-p}b^{n-p}+a^{n-p}b^{m-p})$

نشان داد پس با بررسي اين گروه اثبات به پايان مي رسه. اگر

$m\geq 2n$

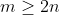باشه داريم:

$\sum_{cyc}(a^mb^n+a^nb^m)=\left ( \sum_{cyc}a^nb^n \right )\left ( \sum_{cyc}a^{m-n} \right )-a^nb^nc^n\sum_{cyc}a^{m-2n}$

و در حالت دوم داريم:

$\sum_{cyc}(a^mb^n+a^nb^m)=\left ( \sum_{cyc}a^nb^n \right )\left ( \sum_{cyc}a^{m-n} \right )-a^{m-n}b^{m-n}c^{m-n}\sum_{cyc}a^{2n-m}b^{2n-m}$

پس با توجه به چيز هايي كه در بالا گفته شد اثبات براي اين گروه هم به پايان مي رسه. دقت كنيد با توجه به متقارن بودن، عبارات ما از اين حالاتي كه گفته شد خارج نيستند.

TheOverlord · 1393/9/12

پاسخ : uvw

در حقیقت چیزی که شما در نظر دارید حالت خاصی از قضیه اساسی چندجمله ای های متقارنه. این قضیه بیان میکنه اگر

$a_i=\sum_{\{x_j_1,x_j_2,\dots,x_j_i\}}x_j_1x_j_2\dots x_j_i$

که

$1 \leq j_i\leq n$

و این اعداد متمایزند، (یعنی در حقیقت

$(x-x_1)(x-x_2)\dots(x-x_n)=x^n+a_1x^{n-1}+\dots+a_n$

) اون وقت هر چند جمله ای متقارن بر حسب

$x_i$

ها رو میشه به فرم رابطه ای از

$ش_i$

$a_i$

ها نوشت.(منظور چند جمله ای با توان صحیح است)

Dadgarnia · 1393/9/12

پاسخ : uvw

TheOverlord گفت

خب اگه اينجوريه يعني هر نامساوي متقارني رو ميشه با uvw حل كرد ديگه پس چرا توي مسابقات معتبر نامساوي متقارن ميدن؟

TheOverlord · 1393/9/12

پاسخ : uvw

مگه uvw معادل درست بودن نامساویه؟(اگه هست بگید چون دقیق نمیدونم!) در ضمن همون طوریش هم کار داره. در ضمن معمولاً تو IMO نامساوی سه متغیره زیاد نبوده چند سال اخیر، و بیشتر به تابعی یا چندجمله ای پرداخته شده، بخاطر همین مسائل uvw و قضایای عدیده و روش های حل متعددی که چند سال اخیر کشف شده خصوصا روش لاگرانژ. و تو مرحله دو هم uvw بدون اثبات مجاز نیست، طوری که آقای math سر جلسه مرحله دو از مراقبشون که آقای عین الله زاده بود پرسیدن.

Dadgarnia · 1393/9/12

پاسخ : uvw

TheOverlord گفت

خب با استفاده از uvw انگار به جاي سه متغير ما دو متغير داريم و اثبات خيلي ساده تر ميشه ولي الان شما سوال انتخاب تيم ايران رو هم نگاه كنين (همين سال آخر) مي بينين كه نامساوي سه متغيره و متقارن داده شده و منظور من فقط IMO نبود.

Dadgarnia · 1393/9/13

پاسخ : uvw

همون سوال TST 2014 ايرانو كه گفتم اينه كه براي اعداد حقيقي و مثبت

$x,y,z$

با شرط

$\sum_{cyc}x^2=\sum_{cyc}x^2y^2$

ثابت كنيد:

$\prod _{cyc}(x-y)^2\leq 2\sum_{cyc}(x^2-y^2)^2$

واضحه كه اين نامساوي متقارنه پس با استفاده از

$uvw$

كافيه نامساوي رو براي

$z=0$

بررسي كنيم كه در اين حالت داريم:

$(x^2+y^2)(x-y)^2=x^2y^2(x-y)^2\leq 2(2x^4-2x^2y^2+2y^4)$

$\Leftrightarrow 3x^4+2x^3y+2xy^3+3y^4\geq 6x^2y^2$

كه اين نامساوي آخر با استفاده از حسابي - هندسي ثابت ميشه.
مي بينين كه هنوز هم از اين سوالا داده ميشه و توي سوالاي TST اكثر كشور ها هم هنوز اينجور نامساوي هايي داده ميشه مگه اين كشور ها دانش آموزاشونو براي رفتن به همين IMO اي كه شما ميگين آماده نمي كنن؟

math1998 · 1393/9/13

پاسخ : uvw

اینو بخونید خالی از لطف نیست!!!

uvw method

math · 1393/9/13

پاسخ : uvw

من با توجه به پست های اخیر شما فکر میکنم برداشتتون از uvw نادرسته ! شما توی هیچ کدوم از راه حل هاتون حالت برابر بودن دو متغیر رو در نظر نگرفتید . در ضمن نوشتن یک عبارت بر حسب u,v,w شرط لازم هست ولی کافی نیست . تابع شما باید بر حسب یکی از

$u,v^{2},w^{3}$

تابعی خطی یا درجه دویی که صعودی باشه یا .... باشد . که خیلی

از نامساوی ها این شرط دوم رو ندارن .

Dadgarnia · 1393/9/13

پاسخ : uvw

math گفت

ممنون از راهنماييتون. مي گفتم چرا اينقدر همه ي نامساوي ها راحت حل ميشن :4: ولي اون سوال tst حالتي كه دو تا برابر باشن خيلي بديهيه!
ما كي مي تونيم فقط دو تا رو برابر بگيريم و كي مي تونيم فقط يكي رو صفر در نظر بگيريم؟ يا هميشه بايد هر دو حالت رو بررسي كنيم؟ در ضمن اين شرط دومي كه گفتين واضحه كه ميشه همه ي نامساوي هاي متقارن با جمله هاي داراي توان صحيح رو به صورت خطي نوشت.

mmahdit · 1393/9/13

پاسخ : uvw

math1998 گفت

فکر می کنم ریشه این تکنیک از Michael Rozenberg باشه که واقعا استاد تمام عیار نامساوی ها توی کالیبر المپیاد هستش.

من هم خواستم یک چیزی در مورد uvw هایی که توی حل سوالات لیگ نوشتی بگم که گفتم بذارم واسه بعد از سه شنبه

پ . ن: به علیرضا دادگرنیا: سعی کن بیشتر با همین حسابی هندسی و کوشی و شور و امثالهم مساله حل کنی تا قضایا و تکنیکای خاص

ضمنا من دوستانه بگم که حیف استعدادت هست که زیادی روی جبر وقت بذاری یه کم هم به هندسه و ترکیبیات برس اونا به لحاظ حجم سوالات توی المپیاد مهم ترن

Dadgarnia · 1393/9/13

پاسخ : uvw

mmahdit گفت

ممنون از راهنماييتون. منم قبلا نامساوي ها رو با نامساوي هاي كلاسيك حل مي كردم ولي از وقتي موفق به حل اولين سوال با uvw شدم گفتم چقدر اين روش خوبه و سر سوال هاي نامساوي ايده ي ديگه اي به ذهنم نميرسه ولي سعي مي كنم از اين به بعد كمتر ازش استفاده كنم.

M_Sharifi · 1393/9/13

پاسخ : uvw

Dadgarnia گفت

همون سوال TST 2014 ايرانو كه گفتم اينه كه براي اعداد حقيقي و مثبت

$x,y,z$

با شرط

$\sum_{cyc}x^2=\sum_{cyc}x^2y^2$

ثابت كنيد:

$\prod _{cyc}(x-y)^2\leq 2\sum_{cyc}(x^2-y^2)^2$

واضحه كه اين نامساوي متقارنه پس با استفاده از

$uvw$

كافيه نامساوي رو براي

$z=0$

بررسي كنيم كه در اين حالت داريم:

$(x^2+y^2)(x-y)^2=x^2y^2(x-y)^2\leq 2(2x^4-2x^2y^2+2y^4)$

$\Leftrightarrow 3x^4+2x^3y+2xy^3+3y^4\geq 6x^2y^2$

كه اين نامساوي آخر با استفاده از حسابي - هندسي ثابت ميشه.
مي بينين كه هنوز هم از اين سوالا داده ميشه و توي سوالاي TST اكثر كشور ها هم هنوز اينجور نامساوي هايي داده ميشه مگه اين كشور ها دانش آموزاشونو براي رفتن به همين IMO اي كه شما ميگين آماده نمي كنن؟

شما دقیقا چطوری توی این سوال از روش uvw استفاده میکنید؟

Dadgarnia · 1393/9/13

پاسخ : uvw

M_Sharifi گفت

مگه این نامساوی متقارن نیست؟ پس با استفاده از قضیه نیوتن میشه بر حسب u,v,w نوشتش. البته آقای بهروز هم شرایط دیگه ای گفتن که من نفهمیدم منظورشون چیه اگه منظورشون رو درست فهمیده باشم این سوال با uvw حل میشه.

math · 1393/9/13

پاسخ : uvw

Dadgarnia گفت

اون سوال tst رو هم من با شما موافقم که با این روش تقریبا !! بدیهی میشه و سوالات مهم تر و معروف تر از اون هم هستن که خیلی راحت با این روش حل میشن !

در تمام مسئله ها باید هر دو حالت بررسی بشه .

در باره شرط دوم هم نوشتنش که خوب با توجه به همون قضیه نیوتن که آقای پویا هم گفتن امکانپذیر ولی این که مثلا اگر درجه دومه باید صعودی باشه که خوب میشه مثال زد که یه چند جمله ای درجه دوم صعودی نباشه .

به نظرم زیاد سمت این چیز ها نرید چون الان uvw هستش یکم که گذشت میبینید یه چیز قوی تر هم هست EMV و بعدش .... اصلا کلا یه مساله مربوط به هیلبرت هستش که اگر اشتباه نکنم آقای صلواتی میگفتن با استفاده از یه الگوریتم زیاد ! میشه هر عبارتی که جمع توابع گویا باشد رو به صورت جمع یکسری مربع کامل نوشت به علاوه یه عبارتی که شرطی داشته باشه :4: خوب برای حل نامساوی ها میشه از یه همچین روش هایی استفاده کرد ! ولی خوب ....

Dadgarnia · 1393/9/13

پاسخ : uvw

math گفت

ممنون! اون ولي خوب تهش براي چيه؟ منظورتون اينه كه نميشه از اين روش ها توي مرحله دو استفاده كرد؟ اون سوال tst هم نوشتم اين شد (البته شما كه گفتين درسته ولي براي اطمينان بيشتر مي نويسم!):

$f(w^3)=3w^6+2u(6u^2-7v^2)w^3+3(4v^6-3u^2v^4+12u^4-16u^2v^2+4v^4)\geq 0$

الان اين درجه دو و صعوديه ديگه؟

M_Sharifi · 1393/9/14

پاسخ : uvw

math گفت

Dadgarnia گفت

روش uvw رو دقیق بخونید. با شرط مساله شما نمیتونید فقط دوتا از متغیرهای u,v,w رو توی سوال ثابت نگه دارید.
مگه یه ترفندهایی بزنید که ...

Dadgarnia · 1393/9/14

پاسخ : uvw

M_Sharifi گفت

آقاي شريفي ميشه كامل روش uvw رو براي من توضيح بدين؟ فكر كنم بايد از پايه و اساس تفكرمو در مورد اين روش عوض كنم :4:.

mmahdit · 1393/9/14

پاسخ : uvw

Dadgarnia گفت

من اگه رسیدم و وقت شد ان شاء الله این مقاله uvw از Mathias Bæk Tejs Knudsen که لینکش همون بالا اومده بود رو ترجمه می کنم و می گذارم روی سایت تا دقیق بخونی

uvw

Dadgarnia

New Member

TheOverlord

New Member

Dadgarnia

New Member

TheOverlord

New Member

Dadgarnia

New Member

Dadgarnia

New Member

math1998

New Member

math

New Member

Dadgarnia

New Member

mmahdit

New Member

Dadgarnia

New Member

M_Sharifi

راهبر ریاضی

Dadgarnia

New Member

math

New Member

Dadgarnia

New Member

M_Sharifi

راهبر ریاضی

Dadgarnia

New Member

mmahdit

New Member