ماراتن هندسه
پاسخ : ماراتن هندسه
فرض می کنیم
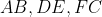 همرسند. بنابر قضیه سوا سینوسی توی مثلث
همرسند. بنابر قضیه سوا سینوسی توی مثلث
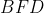 و برای خطوط همرس
و برای خطوط همرس
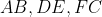 داریم:
داریم:
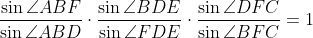 باز هم با استفاده از قضیه سوا سینوسی توی مثلث
باز هم با استفاده از قضیه سوا سینوسی توی مثلث
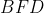 و برای خطوط همرس
و برای خطوط همرس
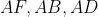 داریم:
داریم:
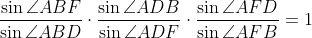 با مقایسه ی دو رابطه ی بدست اومده داریم:
با مقایسه ی دو رابطه ی بدست اومده داریم:
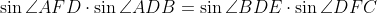 از طرف دیگه داریم:
از طرف دیگه داریم:

 از دو رابطه ی بدست اومده داریم:
از دو رابطه ی بدست اومده داریم:
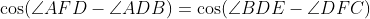 که نتیجه میده
که نتیجه میده
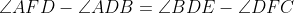 (واضحه که
(واضحه که
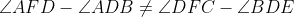 ) پس
) پس
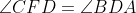 . حالا داریم:
. حالا داریم:
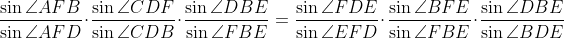
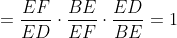 پس با استفاده از قضیه سوا سینوسی در مثلث
پس با استفاده از قضیه سوا سینوسی در مثلث
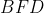 نتیجه می گیریم که
نتیجه می گیریم که
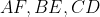 هم همرسند و به طریق مشابه برعکس این هم ثابت میشه.
هم همرسند و به طریق مشابه برعکس این هم ثابت میشه.
---- دو نوشته به هم متصل شده است ----
سوال بعد:
در مثلث
 وسط
وسط
 را
را
 می نامیم. نقطه ی
می نامیم. نقطه ی
 درون مثلث
درون مثلث
 طوری قرار دارد که
طوری قرار دارد که
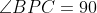 و
و
 و
و
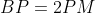 . ثابت کنید
. ثابت کنید
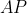 از وسط
از وسط
 می گذرد.
می گذرد.
سوال بعد:
فرض کنید که
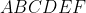 6 ضلعی محدبی باشد که هیچ دو ضلعی از آن موازی نباشند.
6 ضلعی محدبی باشد که هیچ دو ضلعی از آن موازی نباشند.
و داشته باشیم:
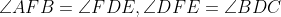 و
و
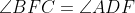 .
.
ثابت کنید خطوط
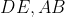 و
و
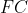 همرسند اگر و تنها اگر خطوط
همرسند اگر و تنها اگر خطوط
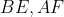 و
و
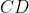 همرس باشند.
همرس باشند.
فرض کنید که
و داشته باشیم:
ثابت کنید خطوط
---- دو نوشته به هم متصل شده است ----
سوال بعد:
در مثلث
پاسخ : ماراتن هندسه
من از یه راه دیگه رفتم c رو نسبت به bp قرینه نکردم ولی از نظر خودم به جواب رسیدم و هم خط بودن a , p , m رو ثابت کردم به طور خلاصه میگمش به طور کلی اول از طریق یه سری برابری کمان ها در دایره ی محیطی a,b,c با امتداد دادن cp , ap و رسم قطر دایره از راس b به چهار ضلعی محاطی abqs رسیدم که q محل برخورد خط bp با مثلث و s محل برخورد قطر رسم شده از b و امتداد ap است و بعد از این قسمت محور اصلی دایره ی محیطی چهار ضلعی محاطی مورد نظر و دایره ی محیطی مثلث رو رسم کردم که براساس یه سری رابطه نتیجه گرفتم که محور اصلی مورد نظر قطر دایره ی محیطی چهار ضلعی محیطی مورد نظر است و از برابری زوایای bsq , aqs به راحتی نتیجه گرفتم که سه نقطه ی خواسته شده هم خط هستند . ( خیلی ببخشید خیلی خلاصه نوشتم فقط نتیجه گیریهامو نوشتم که اگه اشکالی هست بگید تا تصحیحش کنم )
من از یه راه دیگه رفتم c رو نسبت به bp قرینه نکردم ولی از نظر خودم به جواب رسیدم و هم خط بودن a , p , m رو ثابت کردم به طور خلاصه میگمش به طور کلی اول از طریق یه سری برابری کمان ها در دایره ی محیطی a,b,c با امتداد دادن cp , ap و رسم قطر دایره از راس b به چهار ضلعی محاطی abqs رسیدم که q محل برخورد خط bp با مثلث و s محل برخورد قطر رسم شده از b و امتداد ap است و بعد از این قسمت محور اصلی دایره ی محیطی چهار ضلعی محاطی مورد نظر و دایره ی محیطی مثلث رو رسم کردم که براساس یه سری رابطه نتیجه گرفتم که محور اصلی مورد نظر قطر دایره ی محیطی چهار ضلعی محیطی مورد نظر است و از برابری زوایای bsq , aqs به راحتی نتیجه گرفتم که سه نقطه ی خواسته شده هم خط هستند . ( خیلی ببخشید خیلی خلاصه نوشتم فقط نتیجه گیریهامو نوشتم که اگه اشکالی هست بگید تا تصحیحش کنم )
پاسخ : ماراتن هندسه
 وسط
وسط
 هست شما چه جوري ثابت كردين
هست شما چه جوري ثابت كردين
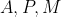 همخطند؟
همخطند؟
من از یه راه دیگه رفتم c رو نسبت به bp قرینه نکردم ولی از نظر خودم به جواب رسیدم و هم خط بودن a , p , m رو ثابت کردم به طور خلاصه میگمش به طور کلی اول از طریق یه سری برابری کمان ها در دایره ی محیطی a,b,c با امتداد دادن cp , ap و رسم قطر دایره از راس b به چهار ضلعی محاطی abqs رسیدم که q محل برخورد خط bp با مثلث و s محل برخورد قطر رسم شده از b و امتداد ap است و بعد از این قسمت محور اصلی دایره ی محیطی چهار ضلعی محاطی مورد نظر و دایره ی محیطی مثلث رو رسم کردم که براساس یه سری رابطه نتیجه گرفتم که محور اصلی مورد نظر قطر دایره ی محیطی چهار ضلعی محیطی مورد نظر است و از برابری زوایای bsq , aqs به راحتی نتیجه گرفتم که سه نقطه ی خواسته شده هم خط هستند . ( خیلی ببخشید خیلی خلاصه نوشتم فقط نتیجه گیریهامو نوشتم که اگه اشکالی هست بگید تا تصحیحش کنم )
پاسخ : ماراتن هندسه
درسته از رابطه ی اون دو تا استفاده نکردم ولی از برابری اون دو زاویه ابتدای راهم استفاده کردم .
ببینید من اول محاطی بودن رو دلیلش رو میگم : ( محل برخورد سر دیگر قطر رسم شده از B با دایره (Q ) است محل برخورد BP با دایره N و محل برخورد CP با دایره S است و محل برخورد AP با دایره رو هم میزارم T.)
از قائمه بودن زاویه ی BAQ استفاده میکنم برای اینکه اثبات کنم کمان های QC , SN با هم برابرند که رابطه هاش برای رسیدنش سادن فقط کافیه بجای AQB زاویه ی برابر ACB را قرار دهیم و یه جا بجای مجموع pbc , pcb 90 توی رابطمون قرار بدیم و در نهایت به اینکه مجموع ABP , ACP برابر با QBC هستند میرسیم که نتیجش میشه برابریه دو کمانی که گفتم و حالا با یه نگاه ساده به شکل میشه فهمید کمان های NQ ,TC با هم برابرند پس دو زاویه ی CAP , PBQ هم با هم برابرند الان میتونیم محاطی بودن چهار ضلعی که قبلا گفتم رو ببینیم . ( البته نام گزاری هام با توضیحی که قبلا دادم فرق میکنه ) و میدونیم که زاویه ی SPB برابر 90 درجه هست و اگه اثبات کنیم APS و BPT متمم هم هستند میشه گفت اون سه نقطه همرس هستند که این رابطه هم از روی کمان های برابر روی دایره ی محیطیمون خیلی ساده بدست میاد . ( فقط قبلش من چهار ضلعیه محاطی رو اثبات کردم تا بتونم از محل برخورد قطراش و متقابل به راس بودنشون برای قسمت آخر استفاده کنم )
میشه شما هم راه حل خودتون رو از راه قرینه کردن بزارید ؟
درسته از رابطه ی اون دو تا استفاده نکردم ولی از برابری اون دو زاویه ابتدای راهم استفاده کردم .
ببینید من اول محاطی بودن رو دلیلش رو میگم : ( محل برخورد سر دیگر قطر رسم شده از B با دایره (Q ) است محل برخورد BP با دایره N و محل برخورد CP با دایره S است و محل برخورد AP با دایره رو هم میزارم T.)
از قائمه بودن زاویه ی BAQ استفاده میکنم برای اینکه اثبات کنم کمان های QC , SN با هم برابرند که رابطه هاش برای رسیدنش سادن فقط کافیه بجای AQB زاویه ی برابر ACB را قرار دهیم و یه جا بجای مجموع pbc , pcb 90 توی رابطمون قرار بدیم و در نهایت به اینکه مجموع ABP , ACP برابر با QBC هستند میرسیم که نتیجش میشه برابریه دو کمانی که گفتم و حالا با یه نگاه ساده به شکل میشه فهمید کمان های NQ ,TC با هم برابرند پس دو زاویه ی CAP , PBQ هم با هم برابرند الان میتونیم محاطی بودن چهار ضلعی که قبلا گفتم رو ببینیم . ( البته نام گزاری هام با توضیحی که قبلا دادم فرق میکنه ) و میدونیم که زاویه ی SPB برابر 90 درجه هست و اگه اثبات کنیم APS و BPT متمم هم هستند میشه گفت اون سه نقطه همرس هستند که این رابطه هم از روی کمان های برابر روی دایره ی محیطیمون خیلی ساده بدست میاد . ( فقط قبلش من چهار ضلعیه محاطی رو اثبات کردم تا بتونم از محل برخورد قطراش و متقابل به راس بودنشون برای قسمت آخر استفاده کنم )
میشه شما هم راه حل خودتون رو از راه قرینه کردن بزارید ؟
آخرین ویرایش توسط مدیر
پاسخ : ماراتن هندسه
موضوع اولتون رو کاملا قبول دارم ولی چیزی که بعدش مطرح کردید رو اصلا اگه بخوایم از این ارتباط طول ها استفاده کنیم دقیقا چجوری میشه آوردش توی راهی که با زاویه سروکار داره ؟ میشه شما راه خودتون با قرینه رو بزارید لطفا ؟؟؟
---- دو نوشته به هم متصل شده است ----
اگه بخوایم از راه قرینه کردن بریم میتونیم بگیم از قرینه کردن C یه چهار ضلعی محاطی به وجود میاد که زوایای رو به رو به ضلع C'B قائمه هستند و با رسم میانه ی نظیر میشه نتیجه گرفت که از هم خط بودن M,P,قرینه ی M' و همچنین نسبت این دو به یکدیگر که 2/3 است این یک میانه است و p مرکز ثقل مثلث M"ACاست و سپس از برابری زاوایا با استفاده از چهار ضلعی محاطی و میانه های رسم شده بر وتر میشه در نهایت با قضیه ی تالس ثابت کرد امتداد میانه ی M"C بر وسط BC برخورد میکند . فکر کنم این جوری باشه .
موضوع اولتون رو کاملا قبول دارم ولی چیزی که بعدش مطرح کردید رو اصلا اگه بخوایم از این ارتباط طول ها استفاده کنیم دقیقا چجوری میشه آوردش توی راهی که با زاویه سروکار داره ؟ میشه شما راه خودتون با قرینه رو بزارید لطفا ؟؟؟
---- دو نوشته به هم متصل شده است ----
اگه بخوایم از راه قرینه کردن بریم میتونیم بگیم از قرینه کردن C یه چهار ضلعی محاطی به وجود میاد که زوایای رو به رو به ضلع C'B قائمه هستند و با رسم میانه ی نظیر میشه نتیجه گرفت که از هم خط بودن M,P,قرینه ی M' و همچنین نسبت این دو به یکدیگر که 2/3 است این یک میانه است و p مرکز ثقل مثلث M"ACاست و سپس از برابری زاوایا با استفاده از چهار ضلعی محاطی و میانه های رسم شده بر وتر میشه در نهایت با قضیه ی تالس ثابت کرد امتداد میانه ی M"C بر وسط BC برخورد میکند . فکر کنم این جوری باشه .
پاسخ : ماراتن هندسه
راهتونو نفهمیدم ولی چیزی که فهمیدم اینه که شما نقطه های زیادی رو بدون علت خاصی به شکل اضافه می کنید که فقط شما رو تو سوال گم می کنه و سوال رو هم حل نمی کنه.
در مورد اون سوالتون که گفتید چه جوری میشه طول ها رو به زاویه ها ربط داد هم جوابش واضحه که با تشابه یا راه های محاسباتی. فکر می کنم زیادی دیگه روی این سوال نسبتا آسون بحث شده و خودم دیگه جوابشو میذارم:
قرینه ی
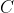 نسبت به
نسبت به
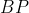 رو
رو
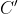 می نامیم. چون
می نامیم. چون
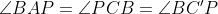 نتیجه می گیریم که چهار ضلعی
نتیجه می گیریم که چهار ضلعی
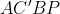 محاطیه و چون
محاطیه و چون
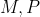 وسط های
وسط های
 هستند طبق تالس نتیجه می گیریم که
هستند طبق تالس نتیجه می گیریم که
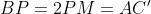 پس
پس
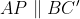 . حالا اگه
. حالا اگه
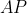 رو امتداد بدیم تا
رو امتداد بدیم تا
 رو توی
رو توی
 قطع کنه چون
قطع کنه چون
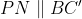 و
و
 وسط
وسط
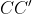 هست نتیجه می گیریم
هست نتیجه می گیریم
 هم وسط
هم وسط
 هست.
هست.
سوال بعد:
در مثلث
 نقاط
نقاط
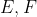 به ترتیب روی
به ترتیب روی
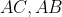 قرار دارند به طوریکه
قرار دارند به طوریکه
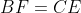 . اگر
. اگر
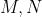 اوساط
اوساط
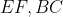 باشند ثابت کنید
باشند ثابت کنید
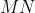 موازی با نیمساز راس
موازی با نیمساز راس
 است.
است.
راهتونو نفهمیدم ولی چیزی که فهمیدم اینه که شما نقطه های زیادی رو بدون علت خاصی به شکل اضافه می کنید که فقط شما رو تو سوال گم می کنه و سوال رو هم حل نمی کنه.
در مورد اون سوالتون که گفتید چه جوری میشه طول ها رو به زاویه ها ربط داد هم جوابش واضحه که با تشابه یا راه های محاسباتی. فکر می کنم زیادی دیگه روی این سوال نسبتا آسون بحث شده و خودم دیگه جوابشو میذارم:
قرینه ی
سوال بعد:
در مثلث
- ارسال ها
- 10
- لایک ها
- 3
- امتیاز
- 0
پاسخ : ماراتن هندسه
B رو نسبت به m قرینه می کنیم تا p به دست آید. Pc با mn موازی میشه و pe با bf موازی میشه.همچنین pe=ec .
Aep=a. پس cpe=a/2 پس pc با نیمساز زاویه a موازیه. پس mn هم با نیمساز زاویه a موازیه.
سوال بعد(خیلی قشنگه)
مثلث abc مفروض است.نقاط دلخواه x,y,z را به ترتیب روی اضلاع bc,ca,ab انتخاب می کنیم. ثابت کنید ممکن نیست مساحت مثلث xyz از مساحت هم ayz هم bxz و هم cxy کمتر شود.
B رو نسبت به m قرینه می کنیم تا p به دست آید. Pc با mn موازی میشه و pe با bf موازی میشه.همچنین pe=ec .
Aep=a. پس cpe=a/2 پس pc با نیمساز زاویه a موازیه. پس mn هم با نیمساز زاویه a موازیه.
سوال بعد(خیلی قشنگه)
مثلث abc مفروض است.نقاط دلخواه x,y,z را به ترتیب روی اضلاع bc,ca,ab انتخاب می کنیم. ثابت کنید ممکن نیست مساحت مثلث xyz از مساحت هم ayz هم bxz و هم cxy کمتر شود.
پاسخ : ماراتن هندسه
وسط اضلاع
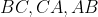 رو به ترتیب
رو به ترتیب
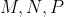 و مرکز دایره محیطی مثلث رو
و مرکز دایره محیطی مثلث رو
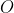 می نامیم. اول ثابت می کنیم اگه نقاط
می نامیم. اول ثابت می کنیم اگه نقاط
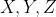 و
و
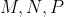 به صورت یه در میون روی اضلاع مثلث قرار نگرفته باشند حکم برقراره. بنابر تقارن می تونیم فرض کنیم
به صورت یه در میون روی اضلاع مثلث قرار نگرفته باشند حکم برقراره. بنابر تقارن می تونیم فرض کنیم
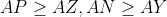 و فاصله ی
و فاصله ی
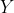 تا
تا
 کوچکتر یا مساوی فاصله
کوچکتر یا مساوی فاصله
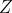 تا
تا
 باشه. اگه
باشه. اگه
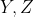 رو ثابت فرض کنیم واضحه که حداقل مساحت مثلث
رو ثابت فرض کنیم واضحه که حداقل مساحت مثلث
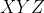 وقتی اتفاق می افته که
وقتی اتفاق می افته که
 روی
روی
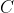 قرار بگیره حالا داریم که مساخت مثلث AYZ بیشتر از مساحت مثلث CYZ هست پس AY بیشتر از CY هست که تناقضه. حالا فرض می کنیم نقاط
قرار بگیره حالا داریم که مساخت مثلث AYZ بیشتر از مساحت مثلث CYZ هست پس AY بیشتر از CY هست که تناقضه. حالا فرض می کنیم نقاط
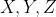 و
و
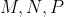 به صورت یه در میون روی اضلاع مثلث قرار گرفته باشند. بنابر تقارن فرض می کنیم
به صورت یه در میون روی اضلاع مثلث قرار گرفته باشند. بنابر تقارن فرض می کنیم
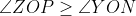 . حالا نقطه ی
. حالا نقطه ی
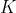 رو روی
رو روی
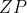 طوری انتخاب می کنیم که
طوری انتخاب می کنیم که
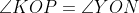 در اینصورت بدست میاد که دو مثلث
در اینصورت بدست میاد که دو مثلث
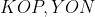 متشابه اند در نتیجه دو مثلث
متشابه اند در نتیجه دو مثلث
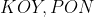 هم متشابه اند حالا داریم:
هم متشابه اند حالا داریم:
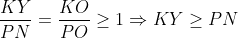 حالا واضحه که
حالا واضحه که
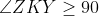 پس
پس
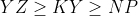 . اگه همینو برای بقیه اضلاع هم بنویسیم بدست میاد
. اگه همینو برای بقیه اضلاع هم بنویسیم بدست میاد
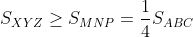 که تناقضه.
که تناقضه.
درسته؟ :7:
---- دو نوشته به هم متصل شده است ----
اگه درسته اینم سوال بعد:
دو دایره
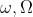 در دو نقطه
در دو نقطه
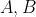 با هم برخورد می کنند. وسط کمان
با هم برخورد می کنند. وسط کمان
 از دایره
از دایره
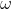 (کمانی که داخل دایره
(کمانی که داخل دایره
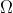 هست) را
هست) را
 می نامیم.
می نامیم.
 نقطه ای دلخواه روی
نقطه ای دلخواه روی
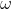 است.
است.
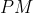 دایره
دایره
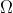 را در
را در
 قطع می کند به طوریکه
قطع می کند به طوریکه
 داخل دایره
داخل دایره
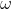 باشد. اگر خط مماس در نقطه
باشد. اگر خط مماس در نقطه
 بر دایره
بر دایره
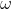 را
را
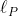 و خط مماس در نقطه
و خط مماس در نقطه
 بر دایره
بر دایره
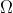 را
را
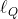 بنامیم ثابت کنید دایره محیطی مثلثی که با خطوط
بنامیم ثابت کنید دایره محیطی مثلثی که با خطوط
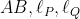 ساخته می شود بر دایره
ساخته می شود بر دایره
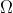 مماس است.
مماس است.
وسط اضلاع
درسته؟ :7:
---- دو نوشته به هم متصل شده است ----
اگه درسته اینم سوال بعد:
دو دایره
آخرین ویرایش توسط مدیر
پاسخ : ماراتن هندسه
حق با شماست. با این روش فقط میشه ثابت کرد یکی از اضلاع مثلث
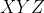 بیشتر از یکی از اضلاع مثلث
بیشتر از یکی از اضلاع مثلث
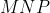 هست. این دیگه فکر کنم درست باشه:
هست. این دیگه فکر کنم درست باشه:
حالت اول که مشابه قبل ثابت میشه. فرض می کنیم اگه از
 شروع کنیم و در جهت عقربه های ساعت روی اضلاع مثلث حر کت کنیم به ترتیب به نقاط
شروع کنیم و در جهت عقربه های ساعت روی اضلاع مثلث حر کت کنیم به ترتیب به نقاط
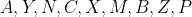 برسیم. هدف اینه که مینیمم مقدار مساحت مثلث
برسیم. هدف اینه که مینیمم مقدار مساحت مثلث
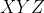 رو حساب کنیم (با شرایطی که گذاشتیم). چون
رو حساب کنیم (با شرایطی که گذاشتیم). چون
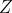 نسبت به
نسبت به
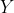 به
به
 نزدیک تره هر چی
نزدیک تره هر چی
 به
به
 نزدیک تر باشه مساحت مثلث
نزدیک تر باشه مساحت مثلث
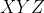 کمتر میشه و اگه همینو برای
کمتر میشه و اگه همینو برای
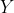 هم بگیم بدست میاد
هم بگیم بدست میاد
 پس حکم ثابت میشه.
پس حکم ثابت میشه.
---- دو نوشته به هم متصل شده است ----
سوال بعد رو دوباره میذارم:
دو دایره
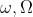 در دو نقطه
در دو نقطه
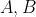 با هم برخورد می کنند. وسط کمان
با هم برخورد می کنند. وسط کمان
 از دایره
از دایره
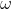 (کمانی که داخل دایره
(کمانی که داخل دایره
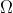 هست) را
هست) را
 می نامیم.
می نامیم.
 نقطه ای دلخواه روی
نقطه ای دلخواه روی
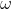 است.
است.
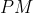 دایره
دایره
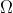 را در
را در
 قطع می کند به طوریکه
قطع می کند به طوریکه
 داخل دایره
داخل دایره
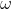 باشد. اگر خط مماس در نقطه
باشد. اگر خط مماس در نقطه
 بر دایره
بر دایره
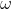 را
را
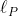 و خط مماس در نقطه
و خط مماس در نقطه
 بر دایره
بر دایره
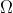 را
را
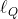 بنامیم ثابت کنید دایره محیطی مثلثی که با خطوط
بنامیم ثابت کنید دایره محیطی مثلثی که با خطوط
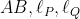 ساخته می شود بر دایره
ساخته می شود بر دایره
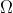 مماس است.
مماس است.
حق با شماست. با این روش فقط میشه ثابت کرد یکی از اضلاع مثلث
حالت اول که مشابه قبل ثابت میشه. فرض می کنیم اگه از
---- دو نوشته به هم متصل شده است ----
سوال بعد رو دوباره میذارم:
دو دایره
پاسخ : ماراتن هندسه
راه حل سوال قبل:
راه خودم با تعمیم بطلمیوس بود که اینجوریه:
محل تقاطع
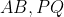 رو
رو
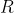 و
و
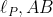 رو
رو
 و
و
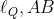 رو
رو
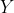 و
و
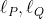 رو
رو
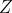 می نامیم. باید ثابت کنیم:
می نامیم. باید ثابت کنیم:



حالا دقت کنید که


رابطه آخر هم بنابر قضیه سینوس ها توی مثلث های
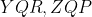 برقراره پس حکم ثابت شد.
برقراره پس حکم ثابت شد.
راه های دیگه رو هم می تونید از اینجا ببینید: Community - Art of Problem Solving
سوال بعد:
در مثلث
 مرکز ارتفاعی را
مرکز ارتفاعی را
 و پای ارتفاع راس
و پای ارتفاع راس
 را
را
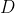 می نامیم. فرض کنید دایره به قطر
می نامیم. فرض کنید دایره به قطر
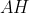 دایره محیطی مثلث را برای بار دوم در
دایره محیطی مثلث را برای بار دوم در
 و
و
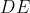 نیز دایره محیطی
نیز دایره محیطی
 را در
را در
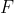 قطع کند. ثابت کنید
قطع کند. ثابت کنید
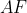 و مماس هایی که از
و مماس هایی که از
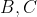 بر دایره محیطی
بر دایره محیطی
 رسم می شوند همرسند.
رسم می شوند همرسند.
راه حل سوال قبل:
راه خودم با تعمیم بطلمیوس بود که اینجوریه:
محل تقاطع
راه های دیگه رو هم می تونید از اینجا ببینید: Community - Art of Problem Solving
سوال بعد:
در مثلث
آخرین ویرایش توسط مدیر
پاسخ : ماراتن هندسه
فرض کنید
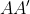 قطر دایره محیطی مثلث و
قطر دایره محیطی مثلث و
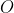 مرکز این دایره باشه و
مرکز این دایره باشه و
 وسط ضلع
وسط ضلع
 .
.
ابتدا ثابت میکنیم که نقاط
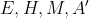 هم خطند.
هم خطند.
 و از طرفی
و از طرفی
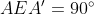 پس
پس
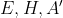 همخطند.
همخطند.
برای اثبات اینکه M روی این خطه محل برخورد AO و HM رو A" در نظر بگیرید.
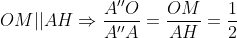 پس A'' روی دایره محیطیه و پس بر A' منطبقه.
پس A'' روی دایره محیطیه و پس بر A' منطبقه.
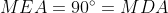 پس
پس
 محاطیه.
محاطیه.
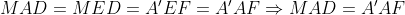
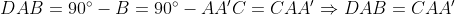 از این دوتا خواهیم داشت:
از این دوتا خواهیم داشت:
 پس AF میانه متقارنه
پس AF میانه متقارنه
پس طبق لمی -") که اثباتش با قضیه سینوسا سخت نیست با مماس های وارد بر دایره محیطی از نقطه های B و C همرسه.
-") که اثباتش با قضیه سینوسا سخت نیست با مماس های وارد بر دایره محیطی از نقطه های B و C همرسه.
---- دو نوشته به هم متصل شده است ----
سوال بعد:
مثلث ABC مفروض است. نقاط
M روی AB
N روی BC
P روی AC
قرار دارند به طوری که
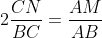 و MN بر NP عموده
و MN بر NP عموده
ثابت کنید که PN نیمساز زاویه MPC است.
سوال بعد:
در مثلث
 مرکز ارتفاعی را
مرکز ارتفاعی را
 و پای ارتفاع راس
و پای ارتفاع راس
 را
را
 می نامیم. فرض کنید دایره به قطر
می نامیم. فرض کنید دایره به قطر
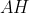 دایره محیطی مثلث را برای بار دوم در
دایره محیطی مثلث را برای بار دوم در
 و
و
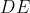 نیز دایره محیطی
نیز دایره محیطی
 را در
را در
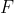 قطع کند. ثابت کنید
قطع کند. ثابت کنید
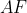 و مماس هایی که از
و مماس هایی که از
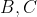 بر دایره محیطی
بر دایره محیطی
 رسم می شوند همرسند.
رسم می شوند همرسند.
در مثلث
ابتدا ثابت میکنیم که نقاط
برای اثبات اینکه M روی این خطه محل برخورد AO و HM رو A" در نظر بگیرید.
پس طبق لمی
---- دو نوشته به هم متصل شده است ----
سوال بعد:
مثلث ABC مفروض است. نقاط
M روی AB
N روی BC
P روی AC
قرار دارند به طوری که
ثابت کنید که PN نیمساز زاویه MPC است.
پاسخ : ماراتن هندسه
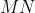 رو امتداد میدیم تا
رو امتداد میدیم تا
 رو توی
رو توی
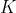 قطع کنه و قرینه ی
قطع کنه و قرینه ی
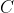 نسبت به
نسبت به
 رو
رو
 می نامیم. حالا چون
می نامیم. حالا چون
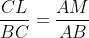 خط
خط
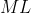 با
با
 موازیه و چون
موازیه و چون
 هم وسط
هم وسط
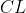 هست چهارضلعی
هست چهارضلعی
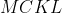 متوازی الاضلاع هست در نتیجه
متوازی الاضلاع هست در نتیجه
 وسط
وسط
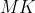 هم هست که حکمو نتیجه میده :4:
هم هست که حکمو نتیجه میده :4:
---- دو نوشته به هم متصل شده است ----
سوال بعد:
مربع های
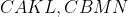 روی اضلاع مثلث حاده الزاویه
روی اضلاع مثلث حاده الزاویه
 و خارج از آن ساخته شده اند.
و خارج از آن ساخته شده اند.
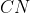 با
با
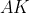 در
در
 و
و
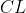 با
با
 در
در
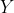 برخورد می کنند.
برخورد می کنند.
 نقطه ای است داخل مثلث و روی دوایر محیطی مثلث های
نقطه ای است داخل مثلث و روی دوایر محیطی مثلث های
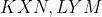 . اگر
. اگر
 وسط
وسط
 باشد ثابت کنید
باشد ثابت کنید
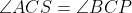 .
.
فرض کنید
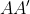 قطر دایره محیطی مثلث و
قطر دایره محیطی مثلث و
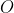 مرکز این دایره باشه و
مرکز این دایره باشه و
 وسط ضلع
وسط ضلع
 .
.
ابتدا ثابت میکنیم که نقاط
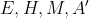 هم خطند.
هم خطند.
 و از طرفی
و از طرفی
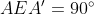 پس
پس
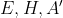 همخطند.
همخطند.
برای اثبات اینکه M روی این خطه محل برخورد AO و HM رو A" در نظر بگیرید.
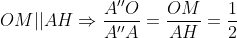 پس A'' روی دایره محیطیه و پس بر A' منطبقه.
پس A'' روی دایره محیطیه و پس بر A' منطبقه.
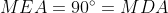 پس
پس
 محاطیه.
محاطیه.
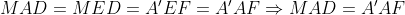
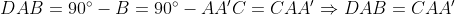 از این دوتا خواهیم داشت:
از این دوتا خواهیم داشت:
 پس AF میانه متقارنه
پس AF میانه متقارنه
پس طبق لمی -") که اثباتش با قضیه سینوسا سخت نیست با مماس های وارد بر دایره محیطی از نقطه های B و C همرسه.
-") که اثباتش با قضیه سینوسا سخت نیست با مماس های وارد بر دایره محیطی از نقطه های B و C همرسه.
---- دو نوشته به هم متصل شده است ----
سوال بعد:
مثلث ABC مفروض است. نقاط
M روی AB
N روی BC
P روی AC
قرار دارند به طوری که
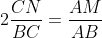 و MN بر NP عموده
و MN بر NP عموده
ثابت کنید که PN نیمساز زاویه MPC است.
ابتدا ثابت میکنیم که نقاط
برای اثبات اینکه M روی این خطه محل برخورد AO و HM رو A" در نظر بگیرید.
پس طبق لمی
---- دو نوشته به هم متصل شده است ----
سوال بعد:
مثلث ABC مفروض است. نقاط
M روی AB
N روی BC
P روی AC
قرار دارند به طوری که
ثابت کنید که PN نیمساز زاویه MPC است.
---- دو نوشته به هم متصل شده است ----
سوال بعد:
مربع های
