سوالي از نامساوي
پاسخ : سوالي از نامساوي
براي n=1,2 به راحتي مي تونيم جوابا رو بدست بياريم پس فرض مي كنيم
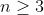 . داريم:
. داريم:
 از نامساوي حسابي مربعي مي دونيم كه
از نامساوي حسابي مربعي مي دونيم كه
 پس بدست مياد:
پس بدست مياد:


 با فرض
با فرض
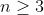 مي دونيم كه
مي دونيم كه
 چون متغير هاي ما اعداد طبيعي هستند بدست مياد:
چون متغير هاي ما اعداد طبيعي هستند بدست مياد:
 باز هم از نامساوي حسابي مربعي بدست مياد
باز هم از نامساوي حسابي مربعي بدست مياد
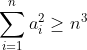 . اگه
. اگه
 بدست مياد:
بدست مياد:
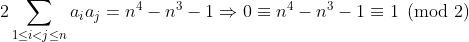 كه تناقضه پس
كه تناقضه پس
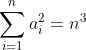 و اين يعني توي نامساوي حسابي مربعي حالت تساوي اتفاق افتاده پس همه ي متغير ها با هم بايد مساوي باشن كه بدست مياد
و اين يعني توي نامساوي حسابي مربعي حالت تساوي اتفاق افتاده پس همه ي متغير ها با هم بايد مساوي باشن كه بدست مياد
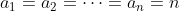 .
.
سلام به همه ي دوستان
براي هر عددطبيعيnتعدادnتايي هاي مرتب
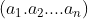 از اعداد صحيح را بيابيد كه:
از اعداد صحيح را بيابيد كه:

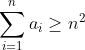
فقط خواهشا اگه ميشه مفصل توضيح بديد.
باتشكر
براي هر عددطبيعيnتعدادnتايي هاي مرتب
فقط خواهشا اگه ميشه مفصل توضيح بديد.
باتشكر
پاسخ : سوالي از نامساوي
ببخشيد فقط من يه چند قسمت رو متوجه نشدم اول اينكه:

عبارت سمت راست چه جور به وجود اومد؟
و در عبارت

چگونه به اين نتيجه رسيديد؟

براي n=1,2 به راحتي مي تونيم جوابا رو بدست بياريم پس فرض مي كنيم
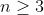 . داريم:
. داريم:
 از نامساوي حسابي مربعي مي دونيم كه
از نامساوي حسابي مربعي مي دونيم كه
 پس بدست مياد:
پس بدست مياد:


 با فرض
با فرض
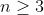 مي دونيم كه
مي دونيم كه
 چون متغير هاي ما اعداد طبيعي هستند بدست مياد:
چون متغير هاي ما اعداد طبيعي هستند بدست مياد:
 باز هم از نامساوي حسابي مربعي بدست مياد
باز هم از نامساوي حسابي مربعي بدست مياد
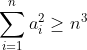 . اگه
. اگه
 بدست مياد:
بدست مياد:
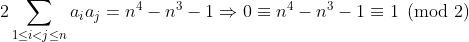 كه تناقضه پس
كه تناقضه پس
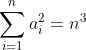 و اين يعني توي نامساوي حسابي مربعي حالت تساوي اتفاق افتاده پس همه ي متغير ها با هم بايد مساوي باشن كه بدست مياد
و اين يعني توي نامساوي حسابي مربعي حالت تساوي اتفاق افتاده پس همه ي متغير ها با هم بايد مساوي باشن كه بدست مياد
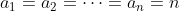 .
.
ببخشيد فقط من يه چند قسمت رو متوجه نشدم اول اينكه:
عبارت سمت راست چه جور به وجود اومد؟
و در عبارت
چگونه به اين نتيجه رسيديد؟
- ارسال ها
- 1,351
- لایک ها
- 1,322
- امتیاز
- 113
پاسخ : سوالي از نامساوي
بله وجود دارد چرا که:
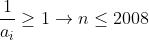
پس دنباله هایی وجود دارند که تعداد عضو های متناهی دارند و کمتر از 2008 است یا مساوی آن که مجموع عضو های دنباله از n^2تجاوز نکندو حال اگر
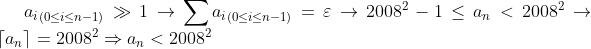
پ.ن:باید مجموع اعضا در شرط مسئله صدق کندو من فق در بالا کرانی را پیدا کردم
درسته؟@Dadgarnia
---- دو نوشته به هم متصل شده است ----
Dadgarnia
نوشته کوتاه نیست
بله وجود دارد چرا که:
پس دنباله هایی وجود دارند که تعداد عضو های متناهی دارند و کمتر از 2008 است یا مساوی آن که مجموع عضو های دنباله از n^2تجاوز نکندو حال اگر
پ.ن:باید مجموع اعضا در شرط مسئله صدق کندو من فق در بالا کرانی را پیدا کردم
درسته؟@Dadgarnia
---- دو نوشته به هم متصل شده است ----
Dadgarnia
نوشته کوتاه نیست
پاسخ : سوالي از نامساوي
حلتون غلطه چون n يه عدد ثابت نيست و دنباله ما هم نامتناهيه. حتي اگه n رو ثابت فرض كنيم براي هر n چنين دنباله اي وجود داره ولي شما براي
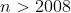 گفتين كه چنين دنباله اي وجود نداره.
گفتين كه چنين دنباله اي وجود نداره.
بله وجود دارد چرا که:
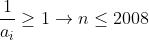
پس دنباله هایی وجود دارند که تعداد عضو های متناهی دارند و کمتر از 2008 است یا مساوی آن که مجموع عضو های دنباله از n^2تجاوز نکندو حال اگر
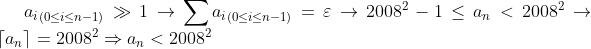
پ.ن:باید مجموع اعضا در شرط مسئله صدق کندو من فق در بالا کرانی را پیدا کردم
درسته؟@Dadgarnia
---- دو نوشته به هم متصل شده است ----
Dadgarnia
نوشته کوتاه نیست
پس دنباله هایی وجود دارند که تعداد عضو های متناهی دارند و کمتر از 2008 است یا مساوی آن که مجموع عضو های دنباله از n^2تجاوز نکندو حال اگر
پ.ن:باید مجموع اعضا در شرط مسئله صدق کندو من فق در بالا کرانی را پیدا کردم
درسته؟@Dadgarnia
---- دو نوشته به هم متصل شده است ----
Dadgarnia
نوشته کوتاه نیست
پاسخ : سوالي از نامساوي
این حل منه:
قرار دهید:


 اون وقت کافیه ثابت کنیم:
اون وقت کافیه ثابت کنیم:
 چون که:
چون که:
 (محاسبات و ساده کردن ها بر عهده خودتون! چیز خاصی نداره!)
(محاسبات و ساده کردن ها بر عهده خودتون! چیز خاصی نداره!)
حالا عبارت سمت چپو باز میکنیم:
 و این هم سادس چون:
و این هم سادس چون:
 و در ادامه :
و در ادامه :

خیلی خلاصه نوشتم فکر کنم!!
** اون تغییر متغیری که نوشتم خیلی کاربردی هست و خیلی هم به درد بخوره**:1:
این حل منه:
قرار دهید:
حالا عبارت سمت چپو باز میکنیم:
+

+


و با استفاده از یه حسابی هندسی ساده:+
خیلی خلاصه نوشتم فکر کنم!!
** اون تغییر متغیری که نوشتم خیلی کاربردی هست و خیلی هم به درد بخوره**:1:
آخرین ویرایش توسط مدیر
