هندسه صفر تا 100
پاسخ : هندسه صفر تا 100
فرض کنید t وسط کمان bc است .با بردار ها ثابت میکنیم pt عمود بر xy است .:

راه 2 :
از p عمود میکنیم بر xyدر n و امتداد میدهیم تا نیمساز زاویه a رو در t قطع کند. اگر r,f,d,l, به ترتیب محل برخورد px,نیمساز راس a و xy,نیمساز راس a و xy,bc و py , نیمساز رای a بنامیم، کافیه اقبات کنیم 4ضلعی rpct محاطیه چون اونوقت tc بر ac ثابت میشه که عموده و در نهایت حکم مساله اثبات میشه.
,mfnt ,dpnm محاطی(mوسط bc) پس زاویه mdp برابر با mft. حالا p رو نسبت به m قرینه میکنیم تا 'p بدست بیاد، داریم :
Md.mt=mf.mp و برای اثبات محاطی بودن rpct باید ثابت کنیم : Mt.mr=mf.mp .
داریم : Mt.mr=mt.ml
با کمی محاسبات بدست میاریم که باید ثابت کنیم cl,pd متوازی هستند. برای اون هم باید ثابت کنیم : Lxyc متوازی الاضلاعه که هست.
(امیدوارم جاییش نا مفهوم نباشه)
فرض کنید t وسط کمان bc است .با بردار ها ثابت میکنیم pt عمود بر xy است .:
راه 2 :
از p عمود میکنیم بر xyدر n و امتداد میدهیم تا نیمساز زاویه a رو در t قطع کند. اگر r,f,d,l, به ترتیب محل برخورد px,نیمساز راس a و xy,نیمساز راس a و xy,bc و py , نیمساز رای a بنامیم، کافیه اقبات کنیم 4ضلعی rpct محاطیه چون اونوقت tc بر ac ثابت میشه که عموده و در نهایت حکم مساله اثبات میشه.
,mfnt ,dpnm محاطی(mوسط bc) پس زاویه mdp برابر با mft. حالا p رو نسبت به m قرینه میکنیم تا 'p بدست بیاد، داریم :
Md.mt=mf.mp و برای اثبات محاطی بودن rpct باید ثابت کنیم : Mt.mr=mf.mp .
داریم : Mt.mr=mt.ml
با کمی محاسبات بدست میاریم که باید ثابت کنیم cl,pd متوازی هستند. برای اون هم باید ثابت کنیم : Lxyc متوازی الاضلاعه که هست.
(امیدوارم جاییش نا مفهوم نباشه)
- ارسال ها
- 194
- لایک ها
- 103
- امتیاز
- 0
پاسخ : هندسه صفر تا 100
داريم

حال محل برخورد EF و AB رو X بگيريد. واضحه كه CEXA و DEXB و CFEDمحاطي اند.در نتيجه
 پس قرينه EF نسبت به ضلع AB همواره از C ميگذره. (در نتيجه خود EF هم از نقطه ثابتي ميگذره ... ؟؟)
پس قرينه EF نسبت به ضلع AB همواره از C ميگذره. (در نتيجه خود EF هم از نقطه ثابتي ميگذره ... ؟؟)
من مطمئن نيستم جمله آخرم درست باشه !! لطفا چك كنيد!!!
نقطه متغیر
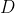 روی کمان بزرگ
روی کمان بزرگ
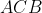 از دایره محیطی مثلث
از دایره محیطی مثلث
 تغییر میکند . نقاط
تغییر میکند . نقاط
 ,
,
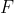 روی
روی
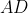 ,
,
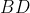 طوری قرار دارند که
طوری قرار دارند که
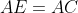 و
و
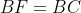 .
.
ثابت کنید با تغییر
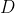 ،
،
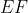 از نقطه ای ثابت میگذرد .
از نقطه ای ثابت میگذرد .
ثابت کنید با تغییر
داريم
حال محل برخورد EF و AB رو X بگيريد. واضحه كه CEXA و DEXB و CFEDمحاطي اند.در نتيجه
من مطمئن نيستم جمله آخرم درست باشه !! لطفا چك كنيد!!!
پاسخ : هندسه صفر تا 100
جمله آخر هم درسته و به طور دقیق تر خطوط ef همدیگر رو در نقطه ی قرینه c نسبت به ab قطع میکنن.
حالا سوال بعدی یکی بزاره دیگه.:3:
داريم

حال محل برخورد ef و ab رو x بگيريد. واضحه كه cexa و dexb و cfedمحاطي اند.در نتيجه
 پس قرينه ef نسبت به ضلع ab همواره از c ميگذره. (در نتيجه خود ef هم از نقطه ثابتي ميگذره ... ؟؟)
پس قرينه ef نسبت به ضلع ab همواره از c ميگذره. (در نتيجه خود ef هم از نقطه ثابتي ميگذره ... ؟؟)
من مطمئن نيستم جمله آخرم درست باشه !! لطفا چك كنيد!!!
حال محل برخورد ef و ab رو x بگيريد. واضحه كه cexa و dexb و cfedمحاطي اند.در نتيجه
من مطمئن نيستم جمله آخرم درست باشه !! لطفا چك كنيد!!!
حالا سوال بعدی یکی بزاره دیگه.:3:
پاسخ : هندسه صفر تا 100
این یه حل ابتدایی : ثابت میکنیم XZ:XY=TY:XY
با رابطه سینوس در میاریم که باید ثابت بشه : PT X.PY
X.PY Z.sinTPY:sinZPX=1
Z.sinTPY:sinZPX=1
داریم :
PT X =PA
X =PA D
D
PY Z=PC
Z=PC B
B
sinTPY:sinZPX=BD:AC
پس در نهایت باید ثابت بشه : PA D.PC
D.PC B.BD:AC=1
B.BD:AC=1
برای این هم داریم
: PA D=RA:RP
D=RA:RP
PC B=RC:RP
B=RC:RP
BD:AC=RB:RC
به این هم توجه میکنیم که : RA.RB=RC.RD=RP^2
(نسبت ها فقط با سینوس به دست آمدند.)
- فرض کنید دایره ای بر دو خط موازی در دو نقطه P,Q مماس است و از نقطه دلخواه R روی خطی که نقطه P روی آن است دو قاطع رسم کردیم که دایره را به ترتیب در نقاط A,B و C,D قطع کرده اند اگر از P به A,B,C,D وصل کنیم تا خط دیگر به ترتیب را در 4 نقطه X,Y,Z,T قطع کنند ثابت کنید:xz=yt
با رابطه سینوس در میاریم که باید ثابت بشه : PT
داریم :
PT
PY
sinTPY:sinZPX=BD:AC
پس در نهایت باید ثابت بشه : PA
برای این هم داریم
: PA
PC
BD:AC=RB:RC
به این هم توجه میکنیم که : RA.RB=RC.RD=RP^2
(نسبت ها فقط با سینوس به دست آمدند.)
- ارسال ها
- 194
- لایک ها
- 103
- امتیاز
- 0
پاسخ : هندسه صفر تا 100
اين سوال قبلا مطرح شده بود
حلش:http://www.irysc.com/forum/t8081-10/#post112092
Mوسط ضلع BCاز مثلثABCاست.خطAMدایره محاطی مثلثABCرا در نقاط L,Kقطع کرده است از L,Kخطهای به موازات BCرسم کرده ایم که دایره محاطی مثلث را برای بار دوم به ترتیب در نقاطY,Xقطع کرده اند . خطهای Ay,AX ضلع BCرا به ترتیب در Q,Pقطع کرده اند ثابت کنید BP=CQ
حلش:http://www.irysc.com/forum/t8081-10/#post112092
پاسخ : هندسه صفر تا 100
راه دوم: از این قضیه یا لم استفاده کنید:i مرکز دایره محاطی و در eبر ab , و در f بر ac و در g بر bc مماسه و m وسط bc است انگاه داریم ig , ef رو روی am قطع میکند.
ادامه حل با تالسو تشابه و کارای جبری حل میشه.
اين سوال قبلا مطرح شده بود
حلش:http://www.irysc.com/forum/t8081-10/#post112092
حلش:http://www.irysc.com/forum/t8081-10/#post112092
ادامه حل با تالسو تشابه و کارای جبری حل میشه.
پاسخ : هندسه صفر تا 100
راه 3 : از دایره ای که از m,p میگذره و بر AB,AC ممای هست استفاده کنید.
راه دوم: از این قضیه یا لم استفاده کنید:i مرکز دایره محاطی و در eبر ab , و در f بر ac و در g بر bc مماسه و m وسط bc است انگاه داریم ig , ef رو روی am قطع میکند.
ادامه حل با تالسو تشابه و کارای جبری حل میشه.
ادامه حل با تالسو تشابه و کارای جبری حل میشه.
پاسخ : هندسه صفر تا 100
منلائوس روی cmf و b-q-e ,, و,, cmf وd-p-n
اینم یه سوال دیگه امید وارم تکراری نباشه:
در چهارضلعی abcd اگر امتداد اضلاع ab,cd همدیگر را در q و امتداد bc,ad همدیگر را در p قطع کنند و اگر یک خط امتداد اضلاع ab,cd,bc,ad را به ترتیب در e,f,m,n قطع کنند به طوری که cd=qf,bc=mp ثابت کنید mn=ef
در چهارضلعی abcd اگر امتداد اضلاع ab,cd همدیگر را در q و امتداد bc,ad همدیگر را در p قطع کنند و اگر یک خط امتداد اضلاع ab,cd,bc,ad را به ترتیب در e,f,m,n قطع کنند به طوری که cd=qf,bc=mp ثابت کنید mn=ef
پاسخ : هندسه صفر تا 100
فکر کنم قبلن توی تاپیک "از مرحله دو تا جهانی" اومده...
{لینکش: http://www.irysc.com/forum/t5841-2/#post86810 }
سوال بعد:
مثلث ABC در دایره w محاط شده خط های مماس بر دایره در نقاط B,C همدیگرو تو T قطع میکنن نقطه S روی BC طوری قرار داره که AT بر AS عموده نقاط 'B و'C طوری روی ST قرار دارن که B'T=BT=C'T (توجه کنید 'C بین 'B و S است) ثابت کنید مثلث های ABC وB'C'A متشابه اند..........:3:
مثلث ABC در دایره w محاط شده خط های مماس بر دایره در نقاط B,C همدیگرو تو T قطع میکنن نقطه S روی BC طوری قرار داره که AT بر AS عموده نقاط 'B و'C طوری روی ST قرار دارن که B'T=BT=C'T (توجه کنید 'C بین 'B و S است) ثابت کنید مثلث های ABC وB'C'A متشابه اند..........:3:
{لینکش: http://www.irysc.com/forum/t5841-2/#post86810 }
آخرین ویرایش توسط مدیر
پاسخ : هندسه صفر تا 100
هه هه هه چه جالب خودم گذاشته بودم...........:4:
حالا یه سوال دیگه:
ABC حاده الزاویه و خطوط مماس بر دایره محیطی آن در B,C همدیگرو تو P قطع میکنن AP دایره محیطی و BC رو به ترتیب در M,D قطع میکنن اگر از D موازی AB رسم کنیم تا PC را در N قطع کند و محل تقاطع AN و BC برابر Q باشد و نقطه X را طوری روی CP در نظر میگیریم که زاویه AQX=180-2C باشد و
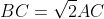 ثابت کنید خط موازی AD از X پاره خط QM را نصف میکند.............:3:
ثابت کنید خط موازی AD از X پاره خط QM را نصف میکند.............:3:
هه هه هه چه جالب خودم گذاشته بودم...........:4:
حالا یه سوال دیگه:
ABC حاده الزاویه و خطوط مماس بر دایره محیطی آن در B,C همدیگرو تو P قطع میکنن AP دایره محیطی و BC رو به ترتیب در M,D قطع میکنن اگر از D موازی AB رسم کنیم تا PC را در N قطع کند و محل تقاطع AN و BC برابر Q باشد و نقطه X را طوری روی CP در نظر میگیریم که زاویه AQX=180-2C باشد و
