پاسخ : ماراتن ترکیبیات
خب حتما دلیلی نداره n امین نفر با اولین یا دومین نفر جا به جا بشه میتونه با قبلی ها جا به جا شه
برای جوابی که شما گفتین مثلا اگه فرض کنیم در یک حالت از n-1 صندلی ،کسی که روی صندلی n-1 هست بیاد روی صندلی 1 بشینه
حالا برای n صندلی، اگه نفر اول در جای خودش بشینه شما گفتین که میشه
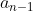 ولی در این حالت فرد n ام نمیتونه بیاد روی صندلی 2 بشینه
ولی در این حالت فرد n ام نمیتونه بیاد روی صندلی 2 بشینه
حالا برای n صندلی، اگه نفر اول در جای خودش بشینه شما گفتین که میشه
