ماراتن نامساوي
پاسخ : ماراتن نامساوي
حالت کلی نامساوی بالا اینه که با همون شرایط بالا و
 داریم:
داریم:

تعریف می کنیم
 می دونیم که
می دونیم که
 پس
پس
 در بازه ی
در بازه ی
 محدبه حالا کافیه روی
محدبه حالا کافیه روی
 ینسن بزنیم:
ینسن بزنیم:
 با قرار دادن
با قرار دادن
 حکم نتیجه میشه.
حکم نتیجه میشه.
---- دو نوشته به هم متصل شده است ----
سوال بعد:
برای اعداد مثبت
 که
که
 نشان دهید:
نشان دهید:

سوال بعد : برای اعداد حقیقی بزرگتر از یک ثابت کنید(همه r ها حقیقی و بزرگتر از یک هستند):

---- دو نوشته به هم متصل شده است ----
سوال بعد:
برای اعداد مثبت
آخرین ویرایش توسط مدیر
- ارسال ها
- 1,351
- لایک ها
- 1,322
- امتیاز
- 113
پاسخ : ماراتن نامساوي
یه راهی دارم که بدون حلیات!
دو تا حالت داریم یا اون اعداد بزرگتر از یکن که بدیهیه!
اگه کوچکتر از یک باشن طرف راست همیشه کوچکتر از یکه ولی طرف چپ بزرگتر از راست است! خوب فک کنم حالت دومو بیشتر حل کنیم بهتره چون حالات خاصی داره به نظرم با جایگشتی حل میشه مگه نه با شرط این که بدترین حالت و بگیریم و اثبات کنیم دسته به نظرتون راهم؟!
---- دو نوشته به هم متصل شده است ----
یه راهی دارم که بدون حلیات!
دو تا حالت داریم یا اون اعداد بزرگتر از یکن که بدیهیه!
اگه کوچکتر از یک باشن طرف راست همیشه کوچکتر از یکه ولی طرف چپ بزرگتر از راست است! خوب فک کنم حالت دومو بیشتر حل کنیم بهتره چون حالات خاصی داره به نظرم با جایگشتی حل میشه مگه نه با شرط این که بدترین حالت و بگیریم و اثبات کنیم دسته به نظرتون راهم؟!
دوستان لطفا یه نفر این سوالو حل کنه! سوال ساده ایه!
دو تا حالت داریم یا اون اعداد بزرگتر از یکن که بدیهیه!
اگه کوچکتر از یک باشن طرف راست همیشه کوچکتر از یکه ولی طرف چپ بزرگتر از راست است! خوب فک کنم حالت دومو بیشتر حل کنیم بهتره چون حالات خاصی داره به نظرم با جایگشتی حل میشه مگه نه با شرط این که بدترین حالت و بگیریم و اثبات کنیم دسته به نظرتون راهم؟!
---- دو نوشته به هم متصل شده است ----
دوستان لطفا یه نفر این سوالو حل کنه! سوال ساده ایه!
دو تا حالت داریم یا اون اعداد بزرگتر از یکن که بدیهیه!
اگه کوچکتر از یک باشن طرف راست همیشه کوچکتر از یکه ولی طرف چپ بزرگتر از راست است! خوب فک کنم حالت دومو بیشتر حل کنیم بهتره چون حالات خاصی داره به نظرم با جایگشتی حل میشه مگه نه با شرط این که بدترین حالت و بگیریم و اثبات کنیم دسته به نظرتون راهم؟!
پاسخ : ماراتن نامساوي
اينجوري كه شما حالت بندي كردين فقط دو حالت براي اون اعداد وجود نداره بيشتر از ده حالت وجود داره! تازه توي حالت دوم واقعا به نظرتون اگه يه همچين چيزي رو توي مرحله دو بنويسيد چند نمره بهتون ميدن؟ كلا نامساوي ها اينجوري حل نميشن مخصوصا كه الان نه تا متغير داريم!
یه راهی دارم که بدون حلیات!
دو تا حالت داریم یا اون اعداد بزرگتر از یکن که بدیهیه!
اگه کوچکتر از یک باشن طرف راست همیشه کوچکتر از یکه ولی طرف چپ بزرگتر از راست است! خوب فک کنم حالت دومو بیشتر حل کنیم بهتره چون حالات خاصی داره به نظرم با جایگشتی حل میشه مگه نه با شرط این که بدترین حالت و بگیریم و اثبات کنیم دسته به نظرتون راهم؟!
---- دو نوشته به هم متصل شده است ----
یه راهی دارم که بدون حلیات!
دو تا حالت داریم یا اون اعداد بزرگتر از یکن که بدیهیه!
اگه کوچکتر از یک باشن طرف راست همیشه کوچکتر از یکه ولی طرف چپ بزرگتر از راست است! خوب فک کنم حالت دومو بیشتر حل کنیم بهتره چون حالات خاصی داره به نظرم با جایگشتی حل میشه مگه نه با شرط این که بدترین حالت و بگیریم و اثبات کنیم دسته به نظرتون راهم؟!
دو تا حالت داریم یا اون اعداد بزرگتر از یکن که بدیهیه!
اگه کوچکتر از یک باشن طرف راست همیشه کوچکتر از یکه ولی طرف چپ بزرگتر از راست است! خوب فک کنم حالت دومو بیشتر حل کنیم بهتره چون حالات خاصی داره به نظرم با جایگشتی حل میشه مگه نه با شرط این که بدترین حالت و بگیریم و اثبات کنیم دسته به نظرتون راهم؟!
---- دو نوشته به هم متصل شده است ----
یه راهی دارم که بدون حلیات!
دو تا حالت داریم یا اون اعداد بزرگتر از یکن که بدیهیه!
اگه کوچکتر از یک باشن طرف راست همیشه کوچکتر از یکه ولی طرف چپ بزرگتر از راست است! خوب فک کنم حالت دومو بیشتر حل کنیم بهتره چون حالات خاصی داره به نظرم با جایگشتی حل میشه مگه نه با شرط این که بدترین حالت و بگیریم و اثبات کنیم دسته به نظرتون راهم؟!
- ارسال ها
- 1,351
- لایک ها
- 1,322
- امتیاز
- 113
پاسخ : ماراتن نامساوي
میخاستم شمارو حرص بدم میدونم اینا اینجوری حل نمیشم ولی نگاهی متفاوت بهشون داشتم و این سوال امکان خیلی کم داره که روز اول طرح بشه و شاید به عنوان سوال 5 میتونه!خوب ببخشین فقط خواستم یه جور دیگه فک کنم که به نتیجه ای میرسم یا نه!:109::205:فک کنم با ارائه حالت تساوی یه دویی بگیرم!
اينجوري كه شما حالت بندي كردين فقط دو حالت براي اون اعداد وجود نداره بيشتر از ده حالت وجود داره! تازه توي حالت دوم واقعا به نظرتون اگه يه همچين چيزي رو توي مرحله دو بنويسيد چند نمره بهتون ميدن؟ كلا نامساوي ها اينجوري حل نميشن مخصوصا كه الان نه تا متغير داريم!
پاسخ : ماراتن نامساوي
میایم یه تغییر متغیر انجام میدیم:

مسئله میشه اینکه بگیم سیگما رادیکال a^2 به فرجه 3 بزرگتر مساویه 2تا رادیکال سیگما ab به فرجه 3 . (ببخشید اینجا رو لاتکس ننوشت! نمیدونم چرا !! )
میایم یه هولدر چهارتایی میزنیم که یه سیگما a تولید شه و رادیکال ها از بین بره:

پس حالا باید بگیم:
 یعنی
یعنی

که اینم حسابی هندسیه چون جمع دوتا پرانتز سمت راستیا رو داریم و حسابی هندسی بزنیم حکم اثبات میشه.
به سوال گذاشتن ادامه بدید! :4:
سول بعد:
براي اعداد مثبت
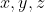 نشان دهيد:
نشان دهيد:

براي اعداد مثبت
مسئله میشه اینکه بگیم سیگما رادیکال a^2 به فرجه 3 بزرگتر مساویه 2تا رادیکال سیگما ab به فرجه 3 . (ببخشید اینجا رو لاتکس ننوشت! نمیدونم چرا !! )
میایم یه هولدر چهارتایی میزنیم که یه سیگما a تولید شه و رادیکال ها از بین بره:
پس حالا باید بگیم:
که اینم حسابی هندسیه چون جمع دوتا پرانتز سمت راستیا رو داریم و حسابی هندسی بزنیم حکم اثبات میشه.
به سوال گذاشتن ادامه بدید! :4:
آخرین ویرایش توسط مدیر
- ارسال ها
- 935
- لایک ها
- 1,654
- امتیاز
- 93
پاسخ : ماراتن نامساوي
طبیعتا دو حالت داریم . x مثبت و y منفی باشه یا اینکه هر مثبت باشند .
در حالت اول که بوضوح طرف چپ نامساوی مثبته . اما در طرف راست xy منفی است . قرینه x+y هم که طبق فرض منفیه پس اون پرانتز منفیه .
 هم مثبته . چون x+y مثبته . اون ورش هم طبق حسابی هندسی بزرگ تر مساوی قدر مطلق xy هست . پس در مجموع طرف راست منفی شد که بدیهی است .
هم مثبته . چون x+y مثبته . اون ورش هم طبق حسابی هندسی بزرگ تر مساوی قدر مطلق xy هست . پس در مجموع طرف راست منفی شد که بدیهی است .
حالا حالتی که هر دو مثبت باشند .
S رو برابر جمع دوعدد و P رو برابر حاصلضرب دو عدد قرار میدیم . ( با استدلالی مشابه میشه نتیجه گرفت که نامساوی رو باید فقط برای حالتی که
 هست اثبات کرد در غیر این صورت طرف راست نامثبت می شود )
هست اثبات کرد در غیر این صورت طرف راست نامثبت می شود )
حالا باید ثابت کنیم :

طبق حسابی هندسی :


پس حالا باید ثابت کنیم :

طبق حسابی هندسی داریم :

پس کافیه بگیم :

یعنی :

در واقع :

که بدیهی است و واضح !
سوال بعد :
برای سه عدد مثبت a,b,c ثابت کنید :

سوال بعد:
براي اعداد حقيقي
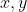 با شرط
با شرط
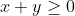 نشان دهيد:
نشان دهيد:

براي اعداد حقيقي
در حالت اول که بوضوح طرف چپ نامساوی مثبته . اما در طرف راست xy منفی است . قرینه x+y هم که طبق فرض منفیه پس اون پرانتز منفیه .
حالا حالتی که هر دو مثبت باشند .
S رو برابر جمع دوعدد و P رو برابر حاصلضرب دو عدد قرار میدیم . ( با استدلالی مشابه میشه نتیجه گرفت که نامساوی رو باید فقط برای حالتی که
حالا باید ثابت کنیم :
طبق حسابی هندسی :
پس حالا باید ثابت کنیم :
طبق حسابی هندسی داریم :
پس کافیه بگیم :
یعنی :
در واقع :
که بدیهی است و واضح !
سوال بعد :
برای سه عدد مثبت a,b,c ثابت کنید :
پاسخ : ماراتن نامساوي
اینجوری درسته؟
میایم رو سه تای اولی کوشی میزنیم:

یعنی باید بگیم:

حالا اگه بگیریم
 باید بگیم
باید بگیم
 و میدونیم که
و میدونیم که
 چون
چون

اگه
 باشه که حکم بدیهیه پس فرض میکنیم که
باشه که حکم بدیهیه پس فرض میکنیم که

حالا میایم حکم جدید رو به توان دو میرسونیم
 یعنی
یعنی
 یعنی باید بگیم
یعنی باید بگیم

میایم حکم رو تجزیه میکنیم.یعنی باید بگیم
 که این هم چون
که این هم چون
 بدیهیه !!
بدیهیه !!
سوال بعد :
برای سه عدد مثبت a,b,c ثابت کنید :
برای سه عدد مثبت a,b,c ثابت کنید :
میایم رو سه تای اولی کوشی میزنیم:
یعنی باید بگیم:
حالا اگه بگیریم
اگه
حالا میایم حکم جدید رو به توان دو میرسونیم
میایم حکم رو تجزیه میکنیم.یعنی باید بگیم
- ارسال ها
- 935
- لایک ها
- 1,654
- امتیاز
- 93
پاسخ : ماراتن نامساوي
بله . راه حل مد نظر من هم همین بود اما تیکه آخرش رو بهتر هم میشد تموم کرد :

به همین راحتی ! بنابر حسابی هندسی !! سوال بعد رو لطف کنید .
اینجوری درسته؟
میایم رو سه تای اولی کوشی میزنیم:

یعنی باید بگیم:

حالا اگه بگیریم
 باید بگیم
باید بگیم
 و میدونیم که
و میدونیم که
 چون
چون

اگه
 باشه که حکم بدیهیه پس فرض میکنیم که
باشه که حکم بدیهیه پس فرض میکنیم که

حالا میایم حکم جدید رو به توان دو میرسونیم
 یعنی
یعنی
 یعنی باید بگیم
یعنی باید بگیم

میایم حکم رو تجزیه میکنیم.یعنی باید بگیم
 که این هم چون
که این هم چون
 بدیهیه !!
بدیهیه !!
میایم رو سه تای اولی کوشی میزنیم:
یعنی باید بگیم:
حالا اگه بگیریم
اگه
حالا میایم حکم جدید رو به توان دو میرسونیم
میایم حکم رو تجزیه میکنیم.یعنی باید بگیم
به همین راحتی ! بنابر حسابی هندسی !! سوال بعد رو لطف کنید .
- ارسال ها
- 935
- لایک ها
- 1,654
- امتیاز
- 93
پاسخ : ماراتن نامساوي
اول باتوجه به نامساوی جایگشتی می دونیم :

حالا دو طرفو ضربدر xyz میکنیم :
حکم :

بنابر حسابی هندسی :



حالا جمع که بزنیم :

پس

و در نهایت

---- دو نوشته به هم متصل شده است ----





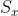

پس نامساوی اثبات شد و حالت تساوی زمانی است که هر سه برابر باشند .
[MENTION=19852]m-saghaei[/MENTION]
سوال بعد:
داریم
 و
و
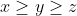 ثابت کنید
ثابت کنید

داریم
حالا دو طرفو ضربدر xyz میکنیم :
حکم :
بنابر حسابی هندسی :
حالا جمع که بزنیم :
پس
و در نهایت
---- دو نوشته به هم متصل شده است ----
یه راه حل دیگه برای این سوال :
از دو طرف عبارت xy + yz + zx رو کم می کنیم .
از دو طرف عبارت xy + yz + zx رو کم می کنیم .
و
طرف چپ به این شکل SOS میشه . طرف راست هم که SOS هست اصلا ! :
پس باید ثابت کنیم :
طرف چپ به این شکل SOS میشه . طرف راست هم که SOS هست اصلا ! :
پس باید ثابت کنیم :
پس اگه ثابت کنیم :
مساله حل میشه .
که خودش مثبت هست پس باید دومی رو بگیم :
پس نامساوی اثبات شد و حالت تساوی زمانی است که هر سه برابر باشند .
[MENTION=19852]m-saghaei[/MENTION]
