ماراتن هندسه version 2
پاسخ : ماراتن هندسه version 2
با تالس تو اضلاع چهارضلعى مستطىل ثابت مىشه بعدش به رلحتى ثابت مىشه 5ضلعى qtefgp محاطى مىشه بعد از محاطى بودن qpgf و s تقاطع gr,qf و محاطى بودن qars,موازى بودن db,gf حکم نتىجه مىشه
راهنمایی : P,f,r روی دایره به قطر eg هستند. نشلان دهید نقطه ای روی ad مثل t وجود دارد که efgt مستطیل است. T نیز روی دایره به قطر eg است. حال نشان دهید q نیز روی این دایره است و سپس زاویه بازی کنید...
پاسخ : ماراتن هندسه version 2
در مثلث حاده الزاویه ی
 ،
،
 وسط
وسط
 ،
،
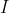 مرکز دایره محاطی داخلی،
مرکز دایره محاطی داخلی،
 و
و
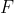 محل تماس این دایره با
محل تماس این دایره با
 و
و
 ،
،
 وسط کمان
وسط کمان
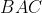 از دایره محیطی مثلث، و
از دایره محیطی مثلث، و
 و
و
 اوساط
اوساط
 و
و
 هستند. محل برخورد
هستند. محل برخورد
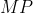 و
و
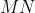 با
با
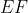 را به ترتیب
را به ترتیب
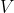 و
و
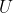 می نامیم. نشان دهید
می نامیم. نشان دهید
 از وسط
از وسط
 می گذرد.
می گذرد.
لطفاً هر کس سوال رو حل کرد سوال بعدی را هم بگذاره و خودتون ماراتن رو به دست بگیرید.
در مثلث حاده الزاویه ی
لطفاً هر کس سوال رو حل کرد سوال بعدی را هم بگذاره و خودتون ماراتن رو به دست بگیرید.
- ارسال ها
- 18
- لایک ها
- 13
- امتیاز
- 3
پاسخ : ماراتن هندسه version 2
لم 1 : Ef و mn و نیمساز راس b در نقطه ی u همرسند . لم 2: در هر چهار ضلعی محاطی abcd اگر q نقطه ی برخورد اقطار چهارضلعی باشد و k وسط ab باشد انگاه qk میانه متقارن نظیر راس q در مثلث cqd میباشد . حالا توجه کنید که i_b , i_c (مراکز محاطی خارجی نظیر راس های cو b ) و b ,c تشکیل چهار ضلعی محاطی میدهند و x وسط i_ai_b میباشد .همچنین چهار ضلعی uvbc نیز محاطی است و iq میانه متقارن ان است .
---- دو نوشته به هم متصل شده است ----
سوال بعد : در مثلث ABC نقاط D , E , F پای ارتفاع های نظیر رئوس A , B ,C مباشند (به ترتیب ) اگر
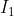 ,
,
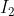 مراکز دایره مجاطی داخلی مثلث های AEF , BFD یاشند و
مراکز دایره مجاطی داخلی مثلث های AEF , BFD یاشند و
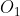 ,
,
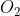 مراکز دوایر محیطی مثلث های
مراکز دوایر محیطی مثلث های
 ,
,
 باشند ثابت کنید :
باشند ثابت کنید :

لم 1 : Ef و mn و نیمساز راس b در نقطه ی u همرسند . لم 2: در هر چهار ضلعی محاطی abcd اگر q نقطه ی برخورد اقطار چهارضلعی باشد و k وسط ab باشد انگاه qk میانه متقارن نظیر راس q در مثلث cqd میباشد . حالا توجه کنید که i_b , i_c (مراکز محاطی خارجی نظیر راس های cو b ) و b ,c تشکیل چهار ضلعی محاطی میدهند و x وسط i_ai_b میباشد .همچنین چهار ضلعی uvbc نیز محاطی است و iq میانه متقارن ان است .
---- دو نوشته به هم متصل شده است ----
سوال بعد : در مثلث ABC نقاط D , E , F پای ارتفاع های نظیر رئوس A , B ,C مباشند (به ترتیب ) اگر
پاسخ : ماراتن هندسه version 2
 را امتداد دهید تا BC,AC را به ترتیب در K,L قطع کنند.چهار ضلعی FKCL محاطیه.اگه تو مثلث های AFL,BFK قضیه نیمساز بنویسیم،نتیجه میشه
را امتداد دهید تا BC,AC را به ترتیب در K,L قطع کنند.چهار ضلعی FKCL محاطیه.اگه تو مثلث های AFL,BFK قضیه نیمساز بنویسیم،نتیجه میشه
 .حالا چون CK=CL ، کافیه ثابت کنیم
.حالا چون CK=CL ، کافیه ثابت کنیم
 .با یکم زاویه بازی هم نتیجه میشه
.با یکم زاویه بازی هم نتیجه میشه
 هم محاطیه.اگه مرکز دایره محیطی این چهار ضلعی رو
هم محاطیه.اگه مرکز دایره محیطی این چهار ضلعی رو
 بنامیم و مرکز دایره محیطی ABC رو O بنامیم،
بنامیم و مرکز دایره محیطی ABC رو O بنامیم،
 .حالا اگه یه کارنو بنویسیم حکم نتیجه میشه.
.حالا اگه یه کارنو بنویسیم حکم نتیجه میشه.
- ارسال ها
- 159
- لایک ها
- 282
- امتیاز
- 0
پاسخ : ماراتن هندسه version 2
PQ را امتداد دهید تا BC را در Z قطع کند. ADZ=A/2+B پس چونZ روی نیمساز AD است DAZ=A/2+B=DAC+CAZ=A/2+ZAC یعنی CAZ=B پس واضحا AZ بر دایره محیطی مثلث ABC مماس است. AYH=ACH و AXH=ABH یعنی AYH-AXH=C-B=180-A-2B=180-2(A/2+B)=180-2ADZ اما Z روی عمود منصف AD است پس AZ=DZ پس AZD=180-2ADZ یعنی AYH-AXH=AZD . دقت کنید که دقیقا یک نقطه با این خاصیت وجود دارد که روی XZ است..حال Y' را طوری در نظر بگیرید که روی XY باشد و ZHY'=ZXA.
چون ZDA متساوی الساقین است پس XZ که عمود منصف است نیمساز هم هست یعنی Y'ZH=AZX پس دو مثلث AZX و Y'ZH متشابهند یعنی AZ/ZX=Y'Z/ZH پس AZ/ZY'=ZX/ZH و AZY'=XZH پس دو مثلث Y'ZA و HZX متشابهند پس Y'AZ=HXZ پس Y'AZ+Y'HZ=AXZ+HXZ=AXH یعنی AY'H=AXZ+HXZ+AZH=AZH+AXH=AZD+AXH اما Y یکتا نقطه ای بود که این خاصیت را داشت پس Y=Y' یعنیAZ/ZX=YZ/ZH یعنی AZ.ZH=ZX.YZ اما AZ=ZD پس ZD.ZH=ZX.ZY پس DHXY محاطی است که حکم مساله است.
سوال بعد: x زاویه ای ثابت است.مثلث متغیر ABC در صفحه را در نظر بگیرید.مثلث های APB و AQC را رو به داخل مثلث ABC ساخته ایم بطوری که PAB=QAC=x و PA=AB و QA=AC. محل برخورد PC و BQ را R بگیرید. فرض کنید O مرکز دایره به قطر R باشد. آنگاه AO/PQ مقداری ثابت است.
PQ را امتداد دهید تا BC را در Z قطع کند. ADZ=A/2+B پس چونZ روی نیمساز AD است DAZ=A/2+B=DAC+CAZ=A/2+ZAC یعنی CAZ=B پس واضحا AZ بر دایره محیطی مثلث ABC مماس است. AYH=ACH و AXH=ABH یعنی AYH-AXH=C-B=180-A-2B=180-2(A/2+B)=180-2ADZ اما Z روی عمود منصف AD است پس AZ=DZ پس AZD=180-2ADZ یعنی AYH-AXH=AZD . دقت کنید که دقیقا یک نقطه با این خاصیت وجود دارد که روی XZ است..حال Y' را طوری در نظر بگیرید که روی XY باشد و ZHY'=ZXA.
چون ZDA متساوی الساقین است پس XZ که عمود منصف است نیمساز هم هست یعنی Y'ZH=AZX پس دو مثلث AZX و Y'ZH متشابهند یعنی AZ/ZX=Y'Z/ZH پس AZ/ZY'=ZX/ZH و AZY'=XZH پس دو مثلث Y'ZA و HZX متشابهند پس Y'AZ=HXZ پس Y'AZ+Y'HZ=AXZ+HXZ=AXH یعنی AY'H=AXZ+HXZ+AZH=AZH+AXH=AZD+AXH اما Y یکتا نقطه ای بود که این خاصیت را داشت پس Y=Y' یعنیAZ/ZX=YZ/ZH یعنی AZ.ZH=ZX.YZ اما AZ=ZD پس ZD.ZH=ZX.ZY پس DHXY محاطی است که حکم مساله است.
سوال بعد: x زاویه ای ثابت است.مثلث متغیر ABC در صفحه را در نظر بگیرید.مثلث های APB و AQC را رو به داخل مثلث ABC ساخته ایم بطوری که PAB=QAC=x و PA=AB و QA=AC. محل برخورد PC و BQ را R بگیرید. فرض کنید O مرکز دایره به قطر R باشد. آنگاه AO/PQ مقداری ثابت است.
آخرین ویرایش توسط مدیر
پاسخ : ماراتن هندسه version 2
اگر وسط های اضلاع ab,ac را m,n بنامیم و وسط نیمساز را k دو مثلث kmx,kpy متشابه اند بقیه سوال یک زاویه بازیست!
راه دیگر: (مخصوص ارس:90 انعکاس به مرکز a وشعاع ab.ac/2 است که نسبت به نیمساز قرینه شود!
انعکاس به مرکز a وشعاع ab.ac/2 است که نسبت به نیمساز قرینه شود!
در مثلثAH,AD، ABC به ترتیب نیمساز و ارتفاع نظیر راس A هستند.عمود منصف AD دایره هایی که به قطر AB,AC رسم میشوند در X,Y قطع میکنند.ثابت کنید XYHD محاطیست.


راه دیگر: (مخصوص ارس:90
- ارسال ها
- 159
- لایک ها
- 282
- امتیاز
- 0
پاسخ : ماراتن هندسه version 2
دوستان سوال جديد ميذارم چون سوال قبلي تاپيك رو خوابونددنبال راه حلش نريد من گذاشتم به اين اميد كه يكي راه حل ساده تر از اون چيزي كه بلدم ارائه بده.
سوال: در چهاروجهي نامسطح abcd وسط قطر هاي ac و bd به ترتيب m و n هستند. ثابت كنيدab=cd و ac=bd و ad=bc اگر و فقط اگر mn بر هر دو قطر عمود باشد.
٢ تا راه ساده هم داره( حداقل)
دوستان سوال جديد ميذارم چون سوال قبلي تاپيك رو خوابونددنبال راه حلش نريد من گذاشتم به اين اميد كه يكي راه حل ساده تر از اون چيزي كه بلدم ارائه بده.
سوال: در چهاروجهي نامسطح abcd وسط قطر هاي ac و bd به ترتيب m و n هستند. ثابت كنيدab=cd و ac=bd و ad=bc اگر و فقط اگر mn بر هر دو قطر عمود باشد.
٢ تا راه ساده هم داره( حداقل)
پاسخ : ماراتن هندسه version 2
---- دو نوشته به هم متصل شده است ----
در مثلث حاده الزاويه
 با اضلاع دو به دو نامساوي
با اضلاع دو به دو نامساوي
 مركز ارتفاعي،
مركز ارتفاعي،
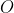 مركز دايره ي محيطي و
مركز دايره ي محيطي و
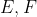 به ترتيب پاي عمود هاي وارد از
به ترتيب پاي عمود هاي وارد از
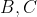 بر اضلاع روبرو مي باشند. خط
بر اضلاع روبرو مي باشند. خط
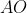 دايره ي محيطي را دوباره در
دايره ي محيطي را دوباره در
 و پاره خط هاي
و پاره خط هاي
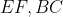 را را به ترتيب در نقاط
را را به ترتيب در نقاط
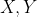 قطع مي كند. اگر
قطع مي كند. اگر
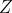 محل برخورد
محل برخورد
 با مماسي كه در
با مماسي كه در
 بر دايره ي محيطي رسم مي شود باشد، ثابت كنيد
بر دايره ي محيطي رسم مي شود باشد، ثابت كنيد
 .
.
سوال بعد:


فرض كنيد
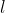 خطي باشه كه در
خطي باشه كه در
 بر دو دايره مماس باشه و
بر دو دايره مماس باشه و
 نقطه اي روي اين خط باشه. مي دونيم كه
نقطه اي روي اين خط باشه. مي دونيم كه
 پس داريم:
پس داريم:
 كه اين هم نتيجه ميده كه چهارضلعي
كه اين هم نتيجه ميده كه چهارضلعي
 محاطيه پس داريم:
محاطيه پس داريم:
 كه حكم رو نتيجه ميده.
كه حكم رو نتيجه ميده.
---- دو نوشته به هم متصل شده است ----
در مثلث حاده الزاويه
پاسخ : ماراتن هندسه version 2
M وسط ضلع BC و T محل برخورد AH ,EF است.
لم:
 هم خطن و
هم خطن و
 .
.
اثبات:هم خطیشون که زیاد سخت نیست.برای اثبات موازی بودن هم:
 .
.
حالا داریم
 که با تقسیم سمت چپ ها بر هم و سمت راست ها بر هم:
که با تقسیم سمت چپ ها بر هم و سمت راست ها بر هم:
 .
.
در مثلث حاده الزاويه
 با اضلاع دو به دو نامساوي
با اضلاع دو به دو نامساوي
 مركز ارتفاعي،
مركز ارتفاعي،
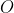 مركز دايره ي محيطي و
مركز دايره ي محيطي و
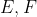 به ترتيب پاي عمود هاي وارد از
به ترتيب پاي عمود هاي وارد از
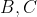 بر اضلاع روبرو مي باشند. خط
بر اضلاع روبرو مي باشند. خط
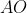 دايره ي محيطي را دوباره در
دايره ي محيطي را دوباره در
 و پاره خط هاي
و پاره خط هاي
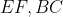 را را به ترتيب در نقاط
را را به ترتيب در نقاط
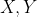 قطع مي كند. اگر
قطع مي كند. اگر
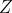 محل برخورد
محل برخورد
 با مماسي كه در
با مماسي كه در
 بر دايره ي محيطي رسم مي شود باشد، ثابت كنيد
بر دايره ي محيطي رسم مي شود باشد، ثابت كنيد
 .
.
لم:
اثبات:هم خطیشون که زیاد سخت نیست.برای اثبات موازی بودن هم:
حالا داریم
آخرین ویرایش توسط مدیر










