ماراتن هندسه
- ارسال ها
- 18
- لایک ها
- 13
- امتیاز
- 3
پاسخ : ماراتن هندسه
مرکز دایره محیطی چهارضلعی HMNO روی عمودمنصف HO و MN قرار دارد که هر دوی این عمودمنصف ها از مرکز دایره ی نه نقطه میگذره . پس یا مرکز دایره نه نقطه مرکز این دایره نیز میباشد که در این حالت به راحتی میتوان ثابت کرد که مثلث قائمه میباشد و ..... در غیر این صورت HMNO باید یک ذوزنقه ی متساوی الساقین باشد که در این حالت HO عمود بر خط گذرنده از روبرو قطری B و راس C خواهد بود که نتیجه میدهدHO عمود منصف این خط است پس مثلث b'HC متساوی الساقین میباشد اکنون از این موضوع که Hb' از وسط AC میگذرد استفاده کنید و حکم را نتیجه بگیرید
مرکز دایره محیطی چهارضلعی HMNO روی عمودمنصف HO و MN قرار دارد که هر دوی این عمودمنصف ها از مرکز دایره ی نه نقطه میگذره . پس یا مرکز دایره نه نقطه مرکز این دایره نیز میباشد که در این حالت به راحتی میتوان ثابت کرد که مثلث قائمه میباشد و ..... در غیر این صورت HMNO باید یک ذوزنقه ی متساوی الساقین باشد که در این حالت HO عمود بر خط گذرنده از روبرو قطری B و راس C خواهد بود که نتیجه میدهدHO عمود منصف این خط است پس مثلث b'HC متساوی الساقین میباشد اکنون از این موضوع که Hb' از وسط AC میگذرد استفاده کنید و حکم را نتیجه بگیرید
- ارسال ها
- 18
- لایک ها
- 13
- امتیاز
- 3
پاسخ : ماراتن هندسه
برای حل سوال نقطه D را روی ضلع BC به گونه ای در نظر بگیرید که داشته باشیم
اکنون با قضیه تالس نشان میدهیم که
. پس باید نشان دهیم که
(که K نقطه برخورد FI با ضلع BC میباشد .) از طرفی :
و
اکنون حکم لازم برای استفاده از تالس را به صورت سینوسی در اورده و تمام زاویه ها را بر حسب c بنویسید و از پس از ساده سازی ها از اتحاد سینوسی زیر استفاده کنید :
برای حل سوال نقطه D را روی ضلع BC به گونه ای در نظر بگیرید که داشته باشیم
- ارسال ها
- 159
- لایک ها
- 282
- امتیاز
- 0
پاسخ : ماراتن هندسه
BQN=BQP+PQN=PMA+PCN=CMA+MCA=180-A پس BQNA محاطي است. به طريق مشابه CQMA هم محاطي است. يعني BQA=BNA=PNA. حال ثابت ميكنيم كه AN/NP=AQ/QB تا در اين صورت طبق برابري يك زاويه و نسبت اضلاع مجاور ANP با AQB متشابه شود و در اين صورت PAN=BAQ كه همان حكم مساله است.
طبق تالس AN/AC=MN/BC=PN/PB پس AN/PN=AC/PB
پس كافيست بگوييم AC/PB=AQ/QB كه معادل است با AC/AQ=BP/BQ كه از تشابه CAQ و PBQ نتيجه ميشود، پس كافيست اين تشابه را ثابت كنيم. اما اين تشابه معادل است با اين كه QBP=QAC و BQP=AQC. اما BQP=PMA=CMA=CQA و QBP=QBN=QAN=QAC طبق چهارضلعي محاطي، پس دو برابري زاويه درستند، كه حكم مساله را نتيجه ميدهد.
سوال بعد: اگرI مركز دايره محاطي داخلي مثلث ABC باشد و Ia مركز دايره محاطي خارجي روبرو به راس A و Xa پاي عمود وارد از Ia بر BC ثابت كنيد IXa از وسط ارتفاع نظير راس A ميگذرد.
BQN=BQP+PQN=PMA+PCN=CMA+MCA=180-A پس BQNA محاطي است. به طريق مشابه CQMA هم محاطي است. يعني BQA=BNA=PNA. حال ثابت ميكنيم كه AN/NP=AQ/QB تا در اين صورت طبق برابري يك زاويه و نسبت اضلاع مجاور ANP با AQB متشابه شود و در اين صورت PAN=BAQ كه همان حكم مساله است.
طبق تالس AN/AC=MN/BC=PN/PB پس AN/PN=AC/PB
پس كافيست بگوييم AC/PB=AQ/QB كه معادل است با AC/AQ=BP/BQ كه از تشابه CAQ و PBQ نتيجه ميشود، پس كافيست اين تشابه را ثابت كنيم. اما اين تشابه معادل است با اين كه QBP=QAC و BQP=AQC. اما BQP=PMA=CMA=CQA و QBP=QBN=QAN=QAC طبق چهارضلعي محاطي، پس دو برابري زاويه درستند، كه حكم مساله را نتيجه ميدهد.
سوال بعد: اگرI مركز دايره محاطي داخلي مثلث ABC باشد و Ia مركز دايره محاطي خارجي روبرو به راس A و Xa پاي عمود وارد از Ia بر BC ثابت كنيد IXa از وسط ارتفاع نظير راس A ميگذرد.
پاسخ : ماراتن هندسه
محل برخورد ارتفاع نظير راس A با BC را H و محل برخورد
با AH را M و محل برخورد AI با BC را D مي ناميم. با نوشتن قضيه ي منلائوس در مثلث AHD داريم:
پس براي اثبات حكم بايد نشان دهيم:
از طرف ديگر با توجه به تشابه مثلث هاي
داريم:
پس بايد نشان دهيم:
كه بنابر قضيه نيمساز صحيح است.
راه همسازي:
را ادامه مي دهيم تا IM را در E قطع كند. براي اثبات حكم كافي است نشان دهيم
. مي دانيم كه
و خطوط
در نقطه ي H همرسند پس چيزي كه مي خواستيم ثابت شد.
محل برخورد ارتفاع نظير راس A با BC را H و محل برخورد
پس براي اثبات حكم بايد نشان دهيم:
از طرف ديگر با توجه به تشابه مثلث هاي
پس بايد نشان دهيم:
كه بنابر قضيه نيمساز صحيح است.
راه همسازي:
آخرین ویرایش توسط مدیر
- ارسال ها
- 159
- لایک ها
- 282
- امتیاز
- 0
پاسخ : ماراتن هندسه
البته این راه خیلی درست نیست چرا که قضایای همسازی که استفاده کرده اید در صورت همخطی درستند، و شما نمیتوانید از درستیشان همخطی را نتیجه بگیرید. همچنین من متوجه استفاده شما از وسط بودن m نمیشوم.
راه همسازي:
را ادامه مي دهيم تا im را در e قطع كند. براي اثبات حكم كافي است نشان دهيم . مي دانيم كه
و خطوط
در نقطه ي h همرسند پس چيزي كه مي خواستيم ثابت شد.
پاسخ : ماراتن هندسه
هم خطی
که از فرض های سواله و E رو هم که روی همین خط مشخص کردم و هم خطی
هم که بدیهیه و قسمت آخر سوالتون رو هم نفهمیدم منظورتون چیه.
---- دو نوشته به هم متصل شده است ----
سوال بعد:
در مثلث ABC،
است. نقطه متغیر D روی پاره خط BC را در نظر بگیرید. فرض کنید
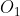مرکز دایره محیطی مثلث ABD و
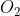مرکز دایره محیطی مثلث ACD باشد. محل تقاطع
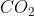و
را M و مرکز دایره محیطی مثلث
را N می نامیم. ثابت کنید خط MN از نقطه ثابتی می گذرد.
هم خطی
---- دو نوشته به هم متصل شده است ----
سوال بعد:
در مثلث ABC،
پاسخ : ماراتن هندسه
AoPS Forum - MN passes through a constant point- Iran NMO 2005 - Problem2 • Art of Problem Solving
سوال بعد:
روی ضلع BC از متوازی الاضلاع ABCD که A حاده است نقطه T را طوری انتخاب میکنیم که ATD حاده الزاویه شود.اگر مراکز دایره های محیطیه ABT,DAT,CDT را به ترتیب X,Y,Z بنامیم نشان دهید مرکز ارتفاعیه XYZ روی AD قرار دارد.
هم خطی
که از فرض های سواله و E رو هم که روی همین خط مشخص کردم و هم خطی
هم که بدیهیه و قسمت آخر سوالتون رو هم نفهمیدم منظورتون چیه.
---- دو نوشته به هم متصل شده است ----
سوال بعد:
در مثلث ABC،
است. نقطه متغیر D روی پاره خط BC را در نظر بگیرید. فرض کنید
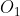مرکز دایره محیطی مثلث ABD و
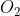مرکز دایره محیطی مثلث ACD باشد. محل تقاطع
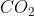و
را M و مرکز دایره محیطی مثلث
را N می نامیم. ثابت کنید خط MN از نقطه ثابتی می گذرد.
---- دو نوشته به هم متصل شده است ----
سوال بعد:
در مثلث ABC،
سوال بعد:
روی ضلع BC از متوازی الاضلاع ABCD که A حاده است نقطه T را طوری انتخاب میکنیم که ATD حاده الزاویه شود.اگر مراکز دایره های محیطیه ABT,DAT,CDT را به ترتیب X,Y,Z بنامیم نشان دهید مرکز ارتفاعیه XYZ روی AD قرار دارد.