مجموعه ی بدون مربع کامل
Aref گفت
من خودم یه راه حل برای مجموعه های متناهی دارم(یعنی تعداد اعضای مجموعه ی مورد نظر مثلا n تا باشه)که از قضیه ی باقی مانده ی چینی استفاده میکنه ولی به نظرم تو مجموعه های نامتناهی به مشکل بر میخوره
mmath گفت
Aref گفت
من خودم یه راه حل برای مجموعه های متناهی دارم(یعنی تعداد اعضای مجموعه ی مورد نظر مثلا n تا باشه)که از قضیه ی باقی مانده ی چینی استفاده میکنه ولی به نظرم تو مجموعه های نامتناهی به مشکل بر میخوره
ثابت کنید مجموعه ای از n عدد طبیعی وجود دارد که مجموع اعضای هیچ زیر مجموعه ای از آن مربع کامل نیست.
اول ثابت میکنیم مجموعه ی
 دستگاه کامل مانده ها نیست.
دستگاه کامل مانده ها نیست.
خب واضحه. از ویلسون حالت کلیش هم به دست میاد که حاصل ضرب هر دو تا جایگشت هم دستگاه کامل مانده ها نیست.
یعنی برای هر عدد اول >2 داریم

یه مجموعه ی n عضوی در نظر میگیریم:

حالا اعداد اول
 رو طوری در نظر میگیریم همشون از n بزرگتر باشند. حالا اگه
رو طوری در نظر میگیریم همشون از n بزرگتر باشند. حالا اگه
 رو متناظر بالا تعریف کنیم، اگه ثابت کنیم دستگاه معادلات هم نهشتی زیر جوابی در اعداد طبیعی دارد مسئله حل می شود.
رو متناظر بالا تعریف کنیم، اگه ثابت کنیم دستگاه معادلات هم نهشتی زیر جوابی در اعداد طبیعی دارد مسئله حل می شود.

اول ثابت میکنیم مجموعه ی
خب واضحه. از ویلسون حالت کلیش هم به دست میاد که حاصل ضرب هر دو تا جایگشت هم دستگاه کامل مانده ها نیست.
یعنی برای هر عدد اول >2 داریم
یه مجموعه ی n عضوی در نظر میگیریم:
حالا اعداد اول
حالا بقیش:
ما ثابت می کنیم که دستگاه معادلات هم نهشتی زیر جواب دارد و حکم اثبات میشود.

فقط کافیه که بگیم:

که t_i ها n تا عددند،
که از قضیه ی اویلر داریم:

یعنی
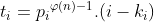 ،و اگه جایگذاری کنیم:
،و اگه جایگذاری کنیم:
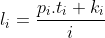 ،کافیه دستگاه معادلات هم نهشتی زیر جوابی در اعداد طبیعی داشته باشد:
،کافیه دستگاه معادلات هم نهشتی زیر جوابی در اعداد طبیعی داشته باشد:

که طبق قضیه ی باقی مانده ی چینی جواب داره. فقط یه چند تا چیز یادم رفت بگم:
 باید متمایز باشند.
باید متمایز باشند.
و این که
 .
.
اثبات کامل شد.
ما ثابت می کنیم که دستگاه معادلات هم نهشتی زیر جواب دارد و حکم اثبات میشود.
فقط کافیه که بگیم:
که t_i ها n تا عددند،
که از قضیه ی اویلر داریم:
یعنی
که طبق قضیه ی باقی مانده ی چینی جواب داره. فقط یه چند تا چیز یادم رفت بگم:
و این که
اثبات کامل شد.
Aref گفت
mmath گفت
Aref گفت
من خودم یه راه حل برای مجموعه های متناهی دارم(یعنی تعداد اعضای مجموعه ی مورد نظر مثلا n تا باشه)که از قضیه ی باقی مانده ی چینی استفاده میکنه ولی به نظرم تو مجموعه های نامتناهی به مشکل بر میخوره








