هندسه صفر تا 100
mrbayat گفت
mahdisaj گفت
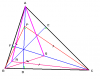
نقطه ی ح را روی ارتفاع AD از مثلث ABC چنان انتخاب می کنیم که BPC=90 .نقاط Q , R را به ترتیب روی ارتفاع های CF,BF ط.ری انتخاب می کنیم که داشته باشیم BQ=BP , CR=CP . ثابت کنید :
AR=AQ
AR=AQ


برای حل این سوال ابتداAK , BC را امتداد می دهیم تا در نقطه ی X همدیگر را قطع کنند . حالا ثابت می کنیم E و F و X هم خط اند.
باید ثابت کنیم منلائوس)
منلائوس)



باید ثابت کنیم
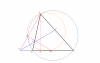
حالا برای چهارضلعی های محاطی AKBC و AKDM قوت نقطه X رو مینویسیم چون دایره به قطر AM است پس AKM=90 و می دانیم ADM=90 پس AKDM محاطی است)
چون دایره به قطر AM است پس AKM=90 و می دانیم ADM=90 پس AKDM محاطی است)



این رابطه رو به دوشکل می نویسیم:
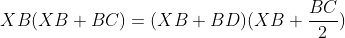
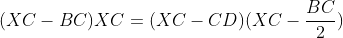
اگه این دوتا رو ساده کنیم به این دوتا رابطه می رسیم:
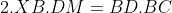
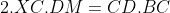
باتقسیم این دو رابطه به هم داریم:
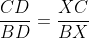
پس حکم ثابت شد.
اگه راه قشنگ تر و بهتری دارید بنویسید چون راهم قشنگ نیست.

اگه راه قشنگ تر و بهتری دارید بنویسید چون راهم قشنگ نیست.

پیوست ها
-
24.8 کیلوبایت بازدیدها 182
[center:40b4e821f7]
 [/center:40b4e821f7]
[/center:40b4e821f7]
من یه سوال راحت می ذارم (هرچند هنوز یه سوال حل نشده.)
خودم دو تا راه حل براش پیدا کردم ببینم شما چند تا دیگه پیدا می کنید؟

در مثلث متساوی الاضلاع ABC نقطه M را روی ضلع AC به طور دلخواه انتخاب می کنیم اگر BC را از طرف C به اندازه ای امتداد دهیم که BM=MN ثابت کنید CN=AM
من یه سوال راحت می ذارم (هرچند هنوز یه سوال حل نشده.)
خودم دو تا راه حل براش پیدا کردم ببینم شما چند تا دیگه پیدا می کنید؟

در مثلث متساوی الاضلاع ABC نقطه M را روی ضلع AC به طور دلخواه انتخاب می کنیم اگر BC را از طرف C به اندازه ای امتداد دهیم که BM=MN ثابت کنید CN=AM
اینم از 5
چون AD نیمساز است پس :

چون l موازی AB است پس :

پس در نتیجه داریم :
 (1)
(1)
به طریق مشابه می توان ثابت کرد :
 (2)
(2)
از 1 و 2 داریم :

از طرفی به راحتی می توان ثابت کرد اگر در مثلثی یک ضلع از ضلع دیگری بزرگنر باشد آنگاه نیمساز وارد بر ضلع بزرگتر از کوچکتر از نیمساز وارد بر ضلع کوچکتر است . پس اگر AC>BC آنگاه BF<AD که تناقض است اگر AC<BC نیز چنین است پس باید [HIGHLIGHT=#ffffff]BC=AC[/HIGHLIGHT]
چون AD نیمساز است پس :
چون l موازی AB است پس :
پس در نتیجه داریم :
به طریق مشابه می توان ثابت کرد :
از 1 و 2 داریم :
از طرفی به راحتی می توان ثابت کرد اگر در مثلثی یک ضلع از ضلع دیگری بزرگنر باشد آنگاه نیمساز وارد بر ضلع بزرگتر از کوچکتر از نیمساز وارد بر ضلع کوچکتر است . پس اگر AC>BC آنگاه BF<AD که تناقض است اگر AC<BC نیز چنین است پس باید [HIGHLIGHT=#ffffff]BC=AC[/HIGHLIGHT]
mahdisaj گفت
Olympiad گفت
[center:24616ec93f]
 [/center:24616ec93f]
[/center:24616ec93f]
راه دوم :

نقطه ی T را به گونه ای انتخاب میکنیم که
 ... حالا از همنهشتی دو مثلث
... حالا از همنهشتی دو مثلث
 و محاطی بودن
و محاطی بودن
 و متساوی الساقین بودن
و متساوی الساقین بودن
مثلث
 استفاده میکنیم ...........
استفاده میکنیم ...........
اگه متوجه نشدید بگید راه حل کامل رو بنویسم ......

راه دوم :

نقطه ی T را به گونه ای انتخاب میکنیم که
مثلث
اگه متوجه نشدید بگید راه حل کامل رو بنویسم ......

چرا مثلث ABN متساوی الساقین است ؟