هندسه صفر تا 100
- ارسال ها
- 95
- لایک ها
- 29
- امتیاز
- 0
mrbayat گفت
[center:a432306bac]

در مثلث
 داریم
داریم
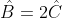 و نقطه ی
و نقطه ی
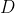 طوری درون مثلث قرار دارد که
طوری درون مثلث قرار دارد که
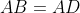 و
و
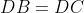 . ثابت کنید:
. ثابت کنید:
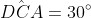
[/center:a432306bac]
- ارسال ها
- 95
- لایک ها
- 29
- امتیاز
- 0
fereidoon گفت
mrbayat گفت
[center:53eda41969]

در مثلث
 داریم
داریم
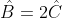 و نقطه ی
و نقطه ی
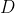 طوری درون مثلث قرار دارد که
طوری درون مثلث قرار دارد که
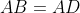 و
و
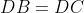 . ثابت کنید:
. ثابت کنید:
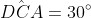
[/center:53eda41969]
اگه راه حلی جز زاویه بازی داره بنویسد

- ارسال ها
- 95
- لایک ها
- 29
- امتیاز
- 0
fereidoon گفت
راه حل منم تا یه جایی مث راه شماست بعدش زاویه بازیه,شما به این نمی گین راه حل کثیف!!!!!!!!! من که می گم



IMOgoldmedal گفت
[center:3944230d9c][HIGHLIGHT=#e36c09]9 [/HIGHLIGHT][/center:3944230d9c]
در مثلث
 مي دانيم
مي دانيم
 . خطي كه از
. خطي كه از
 نقطه وسط ضلع
نقطه وسط ضلع
 موازي نيمساز زاويه
موازي نيمساز زاويه
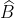 رسم مي شود ضلع
رسم مي شود ضلع
 را در نقطه
را در نقطه
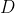 قطع مي كند. نشان دهيد
قطع مي كند. نشان دهيد
 . حل بفرماييد
. حل بفرماييد
در مثلث
پای نیمساز زاویه B را P می نامیم پس :
در نتیجه چون در مثلث ADC میانه ی وارد بر یک ضلع برابر نصف آن ضلع است پس مثلث قایم الزاویه است پس
لطفا بحث تاپیک رو منحرف نکنید
اینم یه سوال مرحله دوم(سال 82)
[center:4d75ad2a5f]

[center:4d75ad2a5f]
زاویه A کوچکترین زاویه ی مثلث ABC است.نقطه ی D روی کمان کوچکتر BC از دایره محیطی مثلث ABC واقع است.عمود منصف های AB و AC با خط AD به ترتیب در نقاط N,M برخورد می نمایند.نقطه T محل برخورد BM و CN است.شعاع دایره محیطی ABC هم برابر R است. ثابت کنید:
 [/center:4d75ad2a5f]
[/center:4d75ad2a5f]



