ماراتن ترکیبیات
پاسخ : ماراتن ترکیبیات
خوشبینانه ترین حالت اینه که هر چهارتایی با همدیگه مستطیل بسازن.فرض کنیم از 2025 بیشتر باشه.طول رو x و عرض رو y میگیریم.میدونیم xy=100 پس:
ولی بنابر نامساوی حسابی هندسی میدونیم:
پس تناقض داره و نتیجه میشه از 2025 نمیتونه بیشتر باشه و اون هم حالتیه که مربع 10*10 باشه که برابر با 2025 میشه.(
)
خوشبینانه ترین حالت اینه که هر چهارتایی با همدیگه مستطیل بسازن.فرض کنیم از 2025 بیشتر باشه.طول رو x و عرض رو y میگیریم.میدونیم xy=100 پس:
ولی بنابر نامساوی حسابی هندسی میدونیم:
پس تناقض داره و نتیجه میشه از 2025 نمیتونه بیشتر باشه و اون هم حالتیه که مربع 10*10 باشه که برابر با 2025 میشه.(
آخرین ویرایش توسط مدیر
پاسخ : ماراتن ترکیبیات
اون یه قضیه دیگست
برای این مسئله میشه این حالت رو بیشترین در نظر گرفت
و مثلا اگه لازم باشه میتونیم بدترین حالت رو 0 مستطیل بگیریم چون امکان نداره کمتر از این باشه
---- دو نوشته به هم متصل شده است ----
سوال n+2 :
به چند طریق میتوان در یک جدول 7x3 ستاره قرار داد به طوری که در هر خانه از جدول حداکثر 1 ستاره و تعداد ستاره ها در هر سطر یا ستون 1،2 یا 3 باشد؟
اون یه قضیه دیگست
برای این مسئله میشه این حالت رو بیشترین در نظر گرفت
و مثلا اگه لازم باشه میتونیم بدترین حالت رو 0 مستطیل بگیریم چون امکان نداره کمتر از این باشه
---- دو نوشته به هم متصل شده است ----
سوال n+2 :
به چند طریق میتوان در یک جدول 7x3 ستاره قرار داد به طوری که در هر خانه از جدول حداکثر 1 ستاره و تعداد ستاره ها در هر سطر یا ستون 1،2 یا 3 باشد؟
پاسخ : ماراتن ترکیبیات
ما حداقل به 7 ستاره (طبق سطر ها) و حدکثر به 9 ستاره (طبق ستون ها) نیازمندیم حالا اگر در هر سطر حداقل یک ستاره وجود داشته باشه پس
یه ستون وجود داره که دقیقا 3 ستاره داره به 3 طریق ستون و
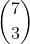طریق خونه ها رو انتخاب میکنیم حالا 4 سطر خالی هنوز داریم 4 تا ستاره میاریم و در 4 سطر و 2 ستون دیگر قرار میدیم
(هر کدوم در یه سطر) فقط باید توجه کنیم 4 ستاره نمیتونن تو یه ستون قرار بگیرن پس روی 3,1 2,2 1,3 حالت بندی میکنیم و مسئله دیگه ساده شد !!!
3,1 : به 4 حالت فقط کافیه اون سطر که ستونش تک ستارس انتخاب کنیم حالا 7 ستاره رو قرار دادیم پس فقط میمونه 7 ستاره باشه یا 8 یا 9 ستاره که اینم راحته!!!!
2 تا حالت دیگه هم مشبه قبلیه!!!!
---- دو نوشته به هم متصل شده است ----
سوال نمیدونم چندم!!!!
مجموعه ای از
نقطه در صفحه است به طوری که هیچ 3 تایی هم خط نیستن برای هر نقطه مثل
از مجموعه
حداقل
نقطه از
وجود دارن که از
هم فاصله ان ثابت کنید :
ما حداقل به 7 ستاره (طبق سطر ها) و حدکثر به 9 ستاره (طبق ستون ها) نیازمندیم حالا اگر در هر سطر حداقل یک ستاره وجود داشته باشه پس
(هر کدوم در یه سطر) فقط باید توجه کنیم 4 ستاره نمیتونن تو یه ستون قرار بگیرن پس روی 3,1 2,2 1,3 حالت بندی میکنیم و مسئله دیگه ساده شد !!!
3,1 : به 4 حالت فقط کافیه اون سطر که ستونش تک ستارس انتخاب کنیم حالا 7 ستاره رو قرار دادیم پس فقط میمونه 7 ستاره باشه یا 8 یا 9 ستاره که اینم راحته!!!!
2 تا حالت دیگه هم مشبه قبلیه!!!!
---- دو نوشته به هم متصل شده است ----
سوال نمیدونم چندم!!!!
آخرین ویرایش توسط مدیر
پاسخ : ماراتن ترکیبیات
سلام
AoPS Forum - shortlist2005 • Art of Problem Solving
---- دو نوشته به هم متصل شده است ----
سلام
IMO 1989
سلام
AoPS Forum - shortlist2005 • Art of Problem Solving
---- دو نوشته به هم متصل شده است ----
ما حداقل به 7 ستاره (طبق سطر ها) و حدکثر به 9 ستاره (طبق ستون ها) نیازمندیم حالا اگر در هر سطر حداقل یک ستاره وجود داشته باشه پس
یه ستون وجود داره که دقیقا 3 ستاره داره به 3 طریق ستون و
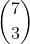طریق خونه ها رو انتخاب میکنیم حالا 4 سطر خالی هنوز داریم 4 تا ستاره میاریم و در 4 سطر و 2 ستون دیگر قرار میدیم
(هر کدوم در یه سطر) فقط باید توجه کنیم 4 ستاره نمیتونن تو یه ستون قرار بگیرن پس روی 3,1 2,2 1,3 حالت بندی میکنیم و مسئله دیگه ساده شد !!!
3,1 : به 4 حالت فقط کافیه اون سطر که ستونش تک ستارس انتخاب کنیم حالا 7 ستاره رو قرار دادیم پس فقط میمونه 7 ستاره باشه یا 8 یا 9 ستاره که اینم راحته!!!!
2 تا حالت دیگه هم مشبه قبلیه!!!!
---- دو نوشته به هم متصل شده است ----
سوال نمیدونم چندم!!!!
مجموعه ای از
نقطه در صفحه است به طوری که هیچ 3 تایی هم خط نیستن برای هر نقطه مثل
از مجموعه
حداقل
نقطه از
وجود دارن که از
هم فاصله ان ثابت کنید :
(هر کدوم در یه سطر) فقط باید توجه کنیم 4 ستاره نمیتونن تو یه ستون قرار بگیرن پس روی 3,1 2,2 1,3 حالت بندی میکنیم و مسئله دیگه ساده شد !!!
3,1 : به 4 حالت فقط کافیه اون سطر که ستونش تک ستارس انتخاب کنیم حالا 7 ستاره رو قرار دادیم پس فقط میمونه 7 ستاره باشه یا 8 یا 9 ستاره که اینم راحته!!!!
2 تا حالت دیگه هم مشبه قبلیه!!!!
---- دو نوشته به هم متصل شده است ----
سوال نمیدونم چندم!!!!
IMO 1989
پاسخ : ماراتن ترکیبیات
سوال بعد:
در یک ردیف
جعبه با شماره های 1 تا
قرار دارند. برای هر
جعبه ای شامل
توپ وجود دارد. هر بار می توانیم تعداد توپ های یک جعبه را با استفاده از توپ های جعبه ای که تعداد توپ بیشتری دارد دو برابر کنیم. ثابت کنید با تکرار این عمل می توان به وضعیتی رسید که برای هر
در جعبه ی
ام دقیقا
توپ قرار داشته باشد.
سوال بعد:
در یک ردیف
پاسخ : ماراتن ترکیبیات
برای جعبه kام میگیم که فرض میکنیم تعداد توپ هاش p باشه
اگه p از k/2 کوچکتر بود اینقدر دوبرابرش میکنیم که از k/2 بزرگتر بشه
حالا میایم جعبه ای رو که ( p - ( k/2 توپ داره رو پیدا میکنیم و و توپ هارو بهش انتقال میدیدم
حالا جعبه kام ما k/2 تا توپ داره که با یه انتقال دیگه دو برابر میکنیمش و میشه k تا
حالا طبق فرض استقرا برای k-1 جعبه دیگه میشه چید
برای جعبه kام میگیم که فرض میکنیم تعداد توپ هاش p باشه
اگه p از k/2 کوچکتر بود اینقدر دوبرابرش میکنیم که از k/2 بزرگتر بشه
حالا میایم جعبه ای رو که ( p - ( k/2 توپ داره رو پیدا میکنیم و و توپ هارو بهش انتقال میدیدم
حالا جعبه kام ما k/2 تا توپ داره که با یه انتقال دیگه دو برابر میکنیمش و میشه k تا
حالا طبق فرض استقرا برای k-1 جعبه دیگه میشه چید
پاسخ : ماراتن ترکیبیات
فرض استقراي ما اينه كه اگه براي هر
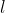كه
جعبه اي با
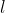توپ وجود داشته باشه اون وقت ميشه كاري كرد كه در جعبه ي
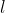ام
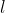تا توپ وجود داشته باشه پس وقتي كه شما اين اعمال رو انجام مي ديد لزومي نداره كه جعبه هامون اين خاصيتي رو كه گفتم داشته باشند مگر اينكه اثباتش كنيد و براي
هاي زوج و فرد بايد جدا اثبات كنيد.
فرض استقراي ما اينه كه اگه براي هر
پاسخ : ماراتن ترکیبیات
میام سوالو دو قسمت میکنیم اگه صفر انتخاب شه و انتخاب نشه
1- اگر صفر انتخاب شه طبق لانه کبوتری حتما یه
داره پس جمش برابر صفره
2- حالا برای این باید ثابت کنیم
فرض کنید x زیر مجموعه ای
از
حکم بالا رو برای همین سوال اثبات کنید
اثباتش با دوستان :87:
سوال بعد:
فرض كنيد
زير مجموعه اي
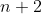از مجموعه ي
باشد. ثابت كنيد سه عضو متمايز a,b,c در
وجود دارند به طوريكه
.
فرض كنيد
1- اگر صفر انتخاب شه طبق لانه کبوتری حتما یه
2- حالا برای این باید ثابت کنیم
فرض کنید x زیر مجموعه ای
اثباتش با دوستان :87:
پاسخ : ماراتن ترکیبیات
فرض کنید
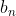تعداد بازآرایی ها باشد.سه حالت وجود دارد.
1-کودک یک در جای خود باقی بماند=
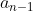
2- 1و2 با هم جابه جا شوند =
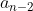
3- همه کودکان یک صندلی به چپ یا راست بروند =2
---- دو نوشته به هم متصل شده است ----
سوال بعد:
آیا یک چند وجهی با تعداد فردی وجه با هر وجه دارای تعداد فردی یال وجود دارد؟؟؟
سوال بعد:
ردیفی دایره ای را از n صندلی در نظر بگیرید.روی هر یک از آنها فردی نشسته است.هر فرد میتواند حداکثر یک صندلی جابه جا شود.تعداد
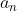روش هایی که آنها میتوانند باز آرایش یابند، را بیابید.
ردیفی دایره ای را از n صندلی در نظر بگیرید.روی هر یک از آنها فردی نشسته است.هر فرد میتواند حداکثر یک صندلی جابه جا شود.تعداد
1-کودک یک در جای خود باقی بماند=
2- 1و2 با هم جابه جا شوند =
3- همه کودکان یک صندلی به چپ یا راست بروند =2
---- دو نوشته به هم متصل شده است ----
سوال بعد:
آیا یک چند وجهی با تعداد فردی وجه با هر وجه دارای تعداد فردی یال وجود دارد؟؟؟
پاسخ : ماراتن ترکیبیات
برای جوابی که شما گفتین مثلا اگه فرض کنیم در یک حالت از n-1 صندلی ،کسی که روی صندلی n-1 هست بیاد روی صندلی 1 بشینه
حالا برای n صندلی، اگه نفر اول در جای خودش بشینه شما گفتین که میشه
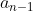ولی در این حالت فرد n ام نمیتونه بیاد روی صندلی 2 بشینه
فرض کنید
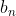تعداد بازآرایی ها باشد.سه حالت وجود دارد.
1-کودک یک در جای خود باقی بماند=
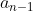
2- 1و2 با هم جابه جا شوند =
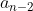
3- همه کودکان یک صندلی به چپ یا راست بروند =2
---- دو نوشته به هم متصل شده است ----
سوال بعد:
آیا یک چند وجهی با تعداد فردی وجه با هر وجه دارای تعداد فردی یال وجود دارد؟؟؟
1-کودک یک در جای خود باقی بماند=
2- 1و2 با هم جابه جا شوند =
3- همه کودکان یک صندلی به چپ یا راست بروند =2
---- دو نوشته به هم متصل شده است ----
سوال بعد:
آیا یک چند وجهی با تعداد فردی وجه با هر وجه دارای تعداد فردی یال وجود دارد؟؟؟
حالا برای n صندلی، اگه نفر اول در جای خودش بشینه شما گفتین که میشه
آخرین ویرایش توسط مدیر