ماراتن ترکیبیات
اينجا يه چيزايي نوشته http://www.4shared.com/file/232231594/81b39f59/0067.html
- ارسال ها
- 2,239
- لایک ها
- 166
- امتیاز
- 0
سوال بیست و هفتم
[center:11475e4ddd]
[/center:11475e4ddd]سوال بیست و هفتم:
الف) به چند طریق می توان یک مستطیلnر×2 را را به وسیله ی مربع های 2×2 و مستطیل های 1×2 پوشاند؟
ب) فرض کنید r و n اعدادی طبیعی باشند. تعداد افرازهای مجموعه ای r عضوی به صورت اجتماعی از n مجموعه ناتهی را با
نمایش می دهیم و آن را r به n مجموعه می خوانیم. این اعداد را اعداد استرلینگ نوع دوم می نامیم. ثابت کنید:
[center:11475e4ddd]
^{k}&space;\binom{n}{k}(n-k)^{r})
[/center:11475e4ddd]
[center:11475e4ddd]
الف) به چند طریق می توان یک مستطیلnر×2 را را به وسیله ی مربع های 2×2 و مستطیل های 1×2 پوشاند؟
ب) فرض کنید r و n اعدادی طبیعی باشند. تعداد افرازهای مجموعه ای r عضوی به صورت اجتماعی از n مجموعه ناتهی را با
[center:11475e4ddd]
- ارسال ها
- 2,239
- لایک ها
- 166
- امتیاز
- 0
[center:4a9414eddb]2[HIGHLIGHT=#000000]7[/HIGHLIGHT][/center:4a9414eddb]
اینها هر دو یکی هستند
وقتی می خواهیم یک شکل رو با چند شکل دیگه بپوشونیم ، می تونیم شکل های دیگر رو دوران بدیم! مثل کف زمین که می خواهند موزاییک کنند.
شاید باید زودتر این نکته رو می گفتم. به هر حال این رو هم در نظر داشته باشید، ناخنتان را هم نجوید!
خیلی خوب می شه اگه راه حل های اشتباه را هم پاک نکنید. چون همان راه حل شما خیلی آموزنده بود، من یک استراتژی جدید از اون یاد گرفتم.
Olympiad گفت
نه ! اوه 1*2 رو با 2*1 اشتباه كردم!!
وقتی می خواهیم یک شکل رو با چند شکل دیگه بپوشونیم ، می تونیم شکل های دیگر رو دوران بدیم! مثل کف زمین که می خواهند موزاییک کنند.
شاید باید زودتر این نکته رو می گفتم. به هر حال این رو هم در نظر داشته باشید، ناخنتان را هم نجوید!
خیلی خوب می شه اگه راه حل های اشتباه را هم پاک نکنید. چون همان راه حل شما خیلی آموزنده بود، من یک استراتژی جدید از اون یاد گرفتم.
27
ما می تونیم i تا خونه عمودی رو حذف کنیم و i تا از n تا انتخاب کنیم
پس نتیجه می گیریم جواب مساوی است با
fn=C(n,0)+c(n,1)+…+c(n,[n/2])=fn-1 + fn-2<?xml:namespace prefix = o ns = "urn:schemas-microsoft-com
fficeffice" /><o></o>
[font=Calibri,sans-serif]<?xml:namespace prefix = v ns = "urn:schemas-microsoft-com:vml" /><v:shapetype id=_x0000_t75 stroked="f" filled="f" path="m@4@5l@4@11@9@11@9@5xe" oreferrelative="t" o:spt="75" coordsize="21600,21600"><v:stroke joinstyle="miter"></v:stroke><v:formulas><v:f eqn="if lineDrawn pixelLineWidth 0"></v:f><v:f eqn="sum @0 1 0"></v:f><v:f eqn="sum 0 0 @1"></v:f><v:f eqn="prod @2 1 2"></v:f><v:f eqn="prod @3 21600 pixelWidth"></v:f><v:f eqn="prod @3 21600 pixelHeight"></v:f><v:f eqn="sum @0 0 1"></v:f><v:f eqn="prod @6 1 2"></v:f><v:f eqn="prod @7 21600 pixelWidth"></v:f><v:f eqn="sum @8 21600 0"></v:f><v:f eqn="prod @7 21600 pixelHeight"></v:f><v:f eqn="sum @10 21600 0"></v:f></v:formulas><vath o:connecttype="rect" gradientshapeok="t" o:extrusionok="f"></vath><o:lock aspectratio="t" v:ext="edit"></o:lock></v:shapetype>[/font]<o></o>
ما می تونیم i تا خونه عمودی رو حذف کنیم و i تا از n تا انتخاب کنیم
پس نتیجه می گیریم جواب مساوی است با
fn=C(n,0)+c(n,1)+…+c(n,[n/2])=fn-1 + fn-2<?xml:namespace prefix = o ns = "urn:schemas-microsoft-com
fficeffice" /><o></o>[font=Calibri,sans-serif]<?xml:namespace prefix = v ns = "urn:schemas-microsoft-com:vml" /><v:shapetype id=_x0000_t75 stroked="f" filled="f" path="m@4@5l@4@11@9@11@9@5xe" o
referrelative="t" o:spt="75" coordsize="21600,21600"><v:stroke joinstyle="miter"></v:stroke><v:formulas><v:f eqn="if lineDrawn pixelLineWidth 0"></v:f><v:f eqn="sum @0 1 0"></v:f><v:f eqn="sum 0 0 @1"></v:f><v:f eqn="prod @2 1 2"></v:f><v:f eqn="prod @3 21600 pixelWidth"></v:f><v:f eqn="prod @3 21600 pixelHeight"></v:f><v:f eqn="sum @0 0 1"></v:f><v:f eqn="prod @6 1 2"></v:f><v:f eqn="prod @7 21600 pixelWidth"></v:f><v:f eqn="sum @8 21600 0"></v:f><v:f eqn="prod @7 21600 pixelHeight"></v:f><v:f eqn="sum @10 21600 0"></v:f></v:formulas><vath o:connecttype="rect" gradientshapeok="t" o:extrusionok="f"></vath><o:lock aspectratio="t" v:ext="edit"></o:lock></v:shapetype>[/font]<o></o>
- ارسال ها
- 2,239
- لایک ها
- 166
- امتیاز
- 0
Olympiad می نویسد:
اگر
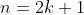آنگاه جواب :
درسته ؟
ببخشید، ولی من هرچی فکر می کنم ، نمی فهمم این از کجا اومد
لطفا کمی توضیح بدهید. ضمنا خیلی راحت تر می شه جواب رو به صورت بازگشتی به دست آورد.
حتما توضیح بدهید
فکر می کنم ایده جالبی پشت این فرمول است!
خیلی جالبه که شما می توانید همه چیز را با ترکیب به این راحتی بیان کنید.
واقعا جای تحسین داره.
اگر
درسته ؟
ببخشید، ولی من هرچی فکر می کنم ، نمی فهمم این از کجا اومد
لطفا کمی توضیح بدهید. ضمنا خیلی راحت تر می شه جواب رو به صورت بازگشتی به دست آورد.
حتما توضیح بدهید
فکر می کنم ایده جالبی پشت این فرمول است!
خیلی جالبه که شما می توانید همه چیز را با ترکیب به این راحتی بیان کنید.
واقعا جای تحسین داره.
- ارسال ها
- 2,239
- لایک ها
- 166
- امتیاز
- 0
قسمت دوم سوال بیست و هفتم
[quote='گوهرشادی][center:475b8776cc]
[/center:475b8776cc]قسمت دوم سوال بیست و هفتم:
ب) فرض کنید r و n اعدادی طبیعی باشند. تعداد افرازهای مجموعه ای r عضوی به صورت اجتماعی از n مجموعه ناتهی را با
نمایش می دهیم و آن را r به n مجموعه می خوانیم. این اعداد را اعداد استرلینگ نوع دوم می نامیم. ثابت کنید:
[center:475b8776cc]
[/center:475b8776cc]
[/quote]
اصل سوال این بود.
[quote='گوهرشادی][center:475b8776cc]
ب) فرض کنید r و n اعدادی طبیعی باشند. تعداد افرازهای مجموعه ای r عضوی به صورت اجتماعی از n مجموعه ناتهی را با
[center:475b8776cc]
[/quote]
اصل سوال این بود.
