ماراتن جبر (سطح پیشرفته)
پاسخ : ماراتن جبر (سطح پیشرفته)
من یه راه حل براش این جا گذاشتم :
http://www.artofproblemsolving.com/Forum/viewtopic.php?p=3391948#p3391948
نکته جالب اینه که این سوال انتخاب تیم ایران سال 2007 بوده و در سال 2005 در ml بیان شده بوده !!!!
http://www.artofproblemsolving.com/...ear=2007&sid=26cbd228531402be110acf1093d3babb
http://www.artofproblemsolving.com/Forum/viewtopic.php?f=38&t=38603
یه راه طولانی تر هم تغییر متغیر x+y=2a[SUP]2[/SUP] و ایده های هندسیه که یکم طولانیه ولی بامزه ست.
همه ی توابع
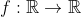 رو پیدا کنید که برای هر x,y حقیقی :
رو پیدا کنید که برای هر x,y حقیقی :

همه ی توابع
http://www.artofproblemsolving.com/Forum/viewtopic.php?p=3391948#p3391948
نکته جالب اینه که این سوال انتخاب تیم ایران سال 2007 بوده و در سال 2005 در ml بیان شده بوده !!!!
http://www.artofproblemsolving.com/...ear=2007&sid=26cbd228531402be110acf1093d3babb
http://www.artofproblemsolving.com/Forum/viewtopic.php?f=38&t=38603
- ارسال ها
- 152
- لایک ها
- 61
- امتیاز
- 0
پاسخ : ماراتن جبر (سطح پیشرفته)
خب جواب من اینه :
اولا اگه دو چند جمله ای معرفی شده در سوال رو به شکل زیر بنویسیم

آنگاه میدانیم اگر مقدار تابع g را در بزرکترین توان x در تابع f قرار ذهیم رگترین توان تابع fog بدست می آید که در ساده ترین شکل حضور دارد(توانی که حتما وجود دارد
حال بزرگترین توان تابع fog یا در واقع درجه ی آن برابر mn است )
در عبارت تابع ترکیبی فوق بزرگترین توان 1393 هست پس
mn=1393
یعنی 4 حالت وجود دارد
m=7 n=199
n=7 m=199
n=1 m=1393
n=1393 m=1
به ازای دو حالت دوم حکم اثبات میشود پس دو حالت اول را رد میکنیم
برای x با توان 1 در fog باید جمله درجه 1 در g در مکان جمله درجه 1 در f قرار گیرد
از طرفی چون در تابع fog جمله ای با توان 199 نداریم و تنها شکل آن جمله درجه 1 در g در مکان جمله درجه 199 در f است پس باید ضریب آن صفر شود اگر چنین حالتی پیش آید جمله ای با درجه 1 در fog نخواهیم داشت پس این حالت غیر قابل قبول است
به همین ترتیب حالت دیگر را رد میکنیم (این بار جمله درجه 199 با ضریب صفر بدست میاید که غ غ ق است و ردمیشود)
و بدین ترتیب حکم ثابت میشود
ببخشید در تعریف g و f جملات درجه صفرو لحاظ نکردم خودتون دقت کنید:15::224:
سوال بعدی:
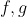 چند جمله ای هایی با ضرایب صحیح هستند که
چند جمله ای هایی با ضرایب صحیح هستند که
 . ثابت کنید درجه ی یکی از این دو چندجمله ای 1 است.
. ثابت کنید درجه ی یکی از این دو چندجمله ای 1 است.
اولا اگه دو چند جمله ای معرفی شده در سوال رو به شکل زیر بنویسیم

آنگاه میدانیم اگر مقدار تابع g را در بزرکترین توان x در تابع f قرار ذهیم رگترین توان تابع fog بدست می آید که در ساده ترین شکل حضور دارد(توانی که حتما وجود دارد
حال بزرگترین توان تابع fog یا در واقع درجه ی آن برابر mn است )
در عبارت تابع ترکیبی فوق بزرگترین توان 1393 هست پس
mn=1393
یعنی 4 حالت وجود دارد
m=7 n=199
n=7 m=199
n=1 m=1393
n=1393 m=1
به ازای دو حالت دوم حکم اثبات میشود پس دو حالت اول را رد میکنیم
برای x با توان 1 در fog باید جمله درجه 1 در g در مکان جمله درجه 1 در f قرار گیرد
از طرفی چون در تابع fog جمله ای با توان 199 نداریم و تنها شکل آن جمله درجه 1 در g در مکان جمله درجه 199 در f است پس باید ضریب آن صفر شود اگر چنین حالتی پیش آید جمله ای با درجه 1 در fog نخواهیم داشت پس این حالت غیر قابل قبول است
به همین ترتیب حالت دیگر را رد میکنیم (این بار جمله درجه 199 با ضریب صفر بدست میاید که غ غ ق است و ردمیشود)
و بدین ترتیب حکم ثابت میشود
ببخشید در تعریف g و f جملات درجه صفرو لحاظ نکردم خودتون دقت کنید:15::224:
آخرین ویرایش توسط مدیر
پاسخ : ماراتن جبر (سطح پیشرفته)
من که نفهمیدم منظورتون از "جمله درجه 1 در g در مکان جمله درجه 1 در f قرار گیرد" چیه؟؟؟
مثلا اگر f درجه 7 باشه اونوقت fog یه چیزی میشه مثل :
 که همه ی جمله هاش میتونن جمله ی درجه 1 تولید کنن و مهم اینه که برایند این جملات چی بشه...
که همه ی جمله هاش میتونن جمله ی درجه 1 تولید کنن و مهم اینه که برایند این جملات چی بشه...
خب جواب من اینه :
اولا اگه دو چند جمله ای معرفی شده در سوال رو به شکل زیر بنویسیم

آنگاه میدانیم اگر مقدار تابع g را در بزرکترین توان x در تابع f قرار ذهیم رگترین توان تابع fog بدست می آید که در ساده ترین شکل حضور دارد(توانی که حتما وجود دارد
حال بزرگترین توان تابع fog یا در واقع درجه ی آن برابر mn است )
در عبارت تابع ترکیبی فوق بزرگترین توان 1393 هست پس
mn=1393
یعنی 4 حالت وجود دارد
m=7 n=199
n=7 m=199
n=1 m=1393
n=1393 m=1
به ازای دو حالت دوم حکم اثبات میشود پس دو حالت اول را رد میکنیم
برای x با توان 1 در fog باید جمله درجه 1 در g در مکان جمله درجه 1 در f قرار گیرد
از طرفی چون در تابع fog جمله ای با توان 199 نداریم و تنها شکل آن جمله درجه 1 در g در مکان جمله درجه 199 در f است پس باید ضریب آن صفر شود اگر چنین حالتی پیش آید جمله ای با درجه 1 در fog نخواهیم داشت پس این حالت غیر قابل قبول است
به همین ترتیب حالت دیگر را رد میکنیم (این بار جمله درجه 199 با ضریب صفر بدست میاید که غ غ ق است و ردمیشود)
و بدین ترتیب حکم ثابت میشود
ببخشید در تعریف g و f جملات درجه صفرو لحاظ نکردم خودتون دقت کنید:15::224:
اولا اگه دو چند جمله ای معرفی شده در سوال رو به شکل زیر بنویسیم

آنگاه میدانیم اگر مقدار تابع g را در بزرکترین توان x در تابع f قرار ذهیم رگترین توان تابع fog بدست می آید که در ساده ترین شکل حضور دارد(توانی که حتما وجود دارد
حال بزرگترین توان تابع fog یا در واقع درجه ی آن برابر mn است )
در عبارت تابع ترکیبی فوق بزرگترین توان 1393 هست پس
mn=1393
یعنی 4 حالت وجود دارد
m=7 n=199
n=7 m=199
n=1 m=1393
n=1393 m=1
به ازای دو حالت دوم حکم اثبات میشود پس دو حالت اول را رد میکنیم
برای x با توان 1 در fog باید جمله درجه 1 در g در مکان جمله درجه 1 در f قرار گیرد
از طرفی چون در تابع fog جمله ای با توان 199 نداریم و تنها شکل آن جمله درجه 1 در g در مکان جمله درجه 199 در f است پس باید ضریب آن صفر شود اگر چنین حالتی پیش آید جمله ای با درجه 1 در fog نخواهیم داشت پس این حالت غیر قابل قبول است
به همین ترتیب حالت دیگر را رد میکنیم (این بار جمله درجه 199 با ضریب صفر بدست میاید که غ غ ق است و ردمیشود)
و بدین ترتیب حکم ثابت میشود
ببخشید در تعریف g و f جملات درجه صفرو لحاظ نکردم خودتون دقت کنید:15::224:
مثلا اگر f درجه 7 باشه اونوقت fog یه چیزی میشه مثل :
پاسخ : ماراتن جبر (سطح پیشرفته)
یه سوال ml کجاست؟
من یه راه حل براش این جا گذاشتم :
AoPS Forum - Nice functional equation • Art of Problem Solving
نکته جالب اینه که این سوال انتخاب تیم ایران سال 2007 بوده و در سال 2005 در ml بیان شده بوده !!!!
Iran Team Selection Test 2007 • Art of Problem Solving
AoPS Forum - f(x^2+y+f(y)) = f(x)^2 + 2y • Art of Problem Solving
AoPS Forum - Nice functional equation • Art of Problem Solving
نکته جالب اینه که این سوال انتخاب تیم ایران سال 2007 بوده و در سال 2005 در ml بیان شده بوده !!!!
Iran Team Selection Test 2007 • Art of Problem Solving
AoPS Forum - f(x^2+y+f(y)) = f(x)^2 + 2y • Art of Problem Solving
- ارسال ها
- 152
- لایک ها
- 61
- امتیاز
- 0
پاسخ : ماراتن جبر (سطح پیشرفته)
منظور جمله ایه که در f یا g توان x در اون یکه
من که نفهمیدم منظورتون از "جمله درجه 1 در g در مکان جمله درجه 1 در f قرار گیرد" چیه؟؟؟
مثلا اگر f درجه 7 باشه اونوقت fog یه چیزی میشه مثل :
 که همه ی جمله هاش میتونن جمله ی درجه 1 تولید کنن و مهم اینه که برایند این جملات چی بشه...
که همه ی جمله هاش میتونن جمله ی درجه 1 تولید کنن و مهم اینه که برایند این جملات چی بشه...
مثلا اگر f درجه 7 باشه اونوقت fog یه چیزی میشه مثل :
پاسخ : ماراتن جبر (سطح پیشرفته)
منظور از جمله درجه یک رو میدونم. اون جا که گفتین در مکان جمله ی درجه 1 f رو نمی فهمم. به بخش دوم پستم دقت کنین شاید مشکل حل بشه. دوباره اینجا می نویسمش:
"مثلا اگر f درجه 7 باشه اونوقت fog یه چیزی میشه مثل :
 که همه ی جمله هاش میتونن جمله ی درجه 1 تولید کنن و مهم اینه که برایند این جملات چی بشه... "
که همه ی جمله هاش میتونن جمله ی درجه 1 تولید کنن و مهم اینه که برایند این جملات چی بشه... "
منظور جمله ایه که در f یا g توان x در اون یکه
"مثلا اگر f درجه 7 باشه اونوقت fog یه چیزی میشه مثل :
پاسخ : ماراتن جبر (سطح پیشرفته)
تا حالا با مینیمال حلی برای این سوال ندیدم. میشه حل کامل بگذارید؟
به علاوه کلاً توی ماراتن ها بهتره حل کامل بگذارید و از لینک دادن و راهنمایی بپرهیزید(بجز کسی که سوال رو گذاشته که میتونه بعد از یک مدتی راهنمایی یا لینک بده).
---- دو نوشته به هم متصل شده است ----
اگر a یک عدد حقیقی باشه f(x) با ضرایب گویا رو چند جمله ای مینیمال a میگن وقتی که بین همه ی چند جمله ای هایی که a ریشه ی اون هاست، f کمترین درجه را داشته باشد. این چند جمله ای خیلی خواص خوبی داره...
راهنمایی :
از خواص چند جمله ایه مینیمال استفاده کنید .
از خواص چند جمله ایه مینیمال استفاده کنید .
به علاوه کلاً توی ماراتن ها بهتره حل کامل بگذارید و از لینک دادن و راهنمایی بپرهیزید(بجز کسی که سوال رو گذاشته که میتونه بعد از یک مدتی راهنمایی یا لینک بده).
---- دو نوشته به هم متصل شده است ----
اینی که گفتید یعنی چی؟
پاسخ : ماراتن جبر (سطح پیشرفته)
خوب اگه مشتق بگیریم میشه:

طبق لم آیزنشتاین :

پس چند جمله ای
 به حاصلضرب دو چند جمله ای با ضرایب صحیح تجزیه نمی شود از طرفی چون f,g صحیح الضرایب هستند و مشتق آنها هم ضرایب صحیح دارد پس یکی از 'f یا 'g باید عدد باشد پس یکی از f یا g درجه یک هستند.
به حاصلضرب دو چند جمله ای با ضرایب صحیح تجزیه نمی شود از طرفی چون f,g صحیح الضرایب هستند و مشتق آنها هم ضرایب صحیح دارد پس یکی از 'f یا 'g باید عدد باشد پس یکی از f یا g درجه یک هستند.
راهنمایی: مشتق بگیرید و از لم آیزنشتاین استفاده کنید.
خوب اگه مشتق بگیریم میشه:
طبق لم آیزنشتاین :
پس چند جمله ای
آخرین ویرایش توسط مدیر
- ارسال ها
- 935
- لایک ها
- 1,654
- امتیاز
- 93
پاسخ : ماراتن جبر (سطح پیشرفته)
در واقع باید اثبات کنیم
 از سه بزرگتر است و از چهار کوچکتراست.
از سه بزرگتر است و از چهار کوچکتراست.
برای قسمت دوم: داریم :
 و همچنین :
و همچنین :
 پس
پس
 پس
پس




 که اینم بزرگ تر مساوی چهار هستش پس آلفا به توان شش از سه بزرگتر است پس براکت آلفا به توان شش میشه سه
که اینم بزرگ تر مساوی چهار هستش پس آلفا به توان شش از سه بزرگتر است پس براکت آلفا به توان شش میشه سه
سوال بعدی(کمی ساده تر از قبلی):
اگر
 ریشه حقیقی چندجمله ای
ریشه حقیقی چندجمله ای
 باشد ثابت کنید :
باشد ثابت کنید :

اگر
برای قسمت دوم: داریم :
