ماراتن جبر (سطح پیشرفته)
- ارسال ها
- 935
- لایک ها
- 1,654
- امتیاز
- 93
پاسخ : ماراتن جبر (سطح پیشرفته)
f تابعی روی اعداد حقیقی است.
[img/]
 [/SIZE][/SIZE][/QUOTE]
[/SIZE][/SIZE][/QUOTE]
اول اثبات می کنیم تابع f پوشا و یک به یک هستش که این راحته . x رو ثابت فرض میکنیم و y رو از منفی بی نهایت یا مثبت بی نهایت تغییر میدیم و بدین ترتیب روی اعداد حقیقی پوشا هستش
فرض می کنیم [IMG]http://latex.codecogs.com/gif.latex?f%28y_%7B1%7D%29%20%3D%20f%28y_%7B2%7D%29 و x رو ثابت میذاریم از اینجا بدست میاد که
 پس یک به یکه.
پس یک به یکه.
چون پوشا هست پس یه k وجود داره که
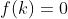 حالا جای x میذاریم k بدست میاد که
حالا جای x میذاریم k بدست میاد که

حالا جای x بذارید صفر بدست میاد که
 پس (f(0 برابر با صفر هستش و چون یک به یکه k=0
پس (f(0 برابر با صفر هستش و چون یک به یکه k=0
حالا به جای x بذارید (f(x طرف چپ همون میشه اما طرف راست میشه
 پس تابع f تابع همانی یا تابع
پس تابع f تابع همانی یا تابع
 هستش
هستش
[img/]
اول اثبات می کنیم تابع f پوشا و یک به یک هستش که این راحته . x رو ثابت فرض میکنیم و y رو از منفی بی نهایت یا مثبت بی نهایت تغییر میدیم و بدین ترتیب روی اعداد حقیقی پوشا هستش
فرض می کنیم [IMG]http://latex.codecogs.com/gif.latex?f%28y_%7B1%7D%29%20%3D%20f%28y_%7B2%7D%29 و x رو ثابت میذاریم از اینجا بدست میاد که
چون پوشا هست پس یه k وجود داره که
حالا جای x بذارید صفر بدست میاد که
حالا به جای x بذارید (f(x طرف چپ همون میشه اما طرف راست میشه
- ارسال ها
- 935
- لایک ها
- 1,654
- امتیاز
- 93
پاسخ : ماراتن جبر (سطح پیشرفته)
یه مشکلی وجود داره تو اثبات من و جناب


 که این تناقضه چرا که f هر عدد یا خودشه یا قرینش اما
که این تناقضه چرا که f هر عدد یا خودشه یا قرینش اما
 نه قرینه
نه قرینه
 هستش نه خودشه پس نتیجه میگیریم f همه اعداد به یک فرم هست.:3::3::3::3:
هستش نه خودشه پس نتیجه میگیریم f همه اعداد به یک فرم هست.:3::3::3::3:
یه مشکلی وجود داره تو اثبات من و جناب
Dadgarnia و اون اینه که الان اثبات شده که ما برای هر x داریم که (f(x یا خود x هستش یا قرینش اما نمیدونیم f همه اعداد به یک فرم هست
بدین منظور فرض میکنیم برای اعداد a,b داریم :
بدین منظور فرض میکنیم برای اعداد a,b داریم :
پاسخ : ماراتن جبر (سطح پیشرفته)
ببخشيد من الان نه فهميدم شما چي رو مي خواين اثبات كنين نه نحوه ي اثباتتونو ميشه يه بار ديگه توضيح بديد
در ضمن كسي نمي خواد سوالي كه من گذاشتمو حل كنه؟
یه مشکلی وجود داره تو اثبات من و جناب


 که این تناقضه چرا که f هر عدد یا خودشه یا قرینش اما
که این تناقضه چرا که f هر عدد یا خودشه یا قرینش اما
 نه قرینه
نه قرینه
 هستش نه خودشه پس نتیجه میگیریم f همه اعداد به یک فرم هست.:3::3::3::3:
هستش نه خودشه پس نتیجه میگیریم f همه اعداد به یک فرم هست.:3::3::3::3:
Dadgarnia و اون اینه که الان اثبات شده که ما برای هر x داریم که (f(x یا خود x هستش یا قرینش اما نمیدونیم f همه اعداد به یک فرم هست
بدین منظور فرض میکنیم برای اعداد a,b داریم :
بدین منظور فرض میکنیم برای اعداد a,b داریم :
در ضمن كسي نمي خواد سوالي كه من گذاشتمو حل كنه؟
پاسخ : ماراتن جبر (سطح پیشرفته)
ببینید معمولا توابع فقط یک ضابطه دارن مگه تعداد خیلی اندکشون حالا شما وقتی به 2 یا بیشتر از یک جواب میرسین باید ثابت کنین که فقط یکی جوابه در واقع باید یکی از جواب ها رو در نظر بگیرید و ادامه بدید تا به تناقض برسید.
ببخشيد من الان نه فهميدم شما چي رو مي خواين اثبات كنين نه نحوه ي اثباتتونو ميشه يه بار ديگه توضيح بديد
در ضمن كسي نمي خواد سوالي كه من گذاشتمو حل كنه؟
در ضمن كسي نمي خواد سوالي كه من گذاشتمو حل كنه؟
- ارسال ها
- 331
- لایک ها
- 264
- امتیاز
- 0
پاسخ : ماراتن جبر (سطح پیشرفته)
مگر سوال قبلي حل شد؟!!! اگر با اون راهنمايي حل شد لطفا اول راه حل و جواب را بگوييد بعد سوال بعدي رو بذاريد. ممنون از لطف شما...
سوال بعد:
 دو چندجمله ای تکین و تجزیه ناپذیر در
دو چندجمله ای تکین و تجزیه ناپذیر در
 هستند.اگرp,q دارای ریشه های
هستند.اگرp,q دارای ریشه های
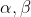 باشند که
باشند که
 نشان دهید چند جمله ای
نشان دهید چند جمله ای
 یک ریشه گویا دارد.
یک ریشه گویا دارد.
این سوال، سوال واقعا قشنگیه(البته به نظر من) و کلا دید من رو نسبت به چندجمله ای عوض کرد.:25:
 (من بعد از حل این سوال:4
(من بعد از حل این سوال:4
این سوال، سوال واقعا قشنگیه(البته به نظر من) و کلا دید من رو نسبت به چندجمله ای عوض کرد.:25:
پاسخ : ماراتن جبر (سطح پیشرفته)
ما بايد تو اينگونه مسائل كه مشخص نكرده ضرايب چند جمله اي ها و ... عضو چه مجموعه اي هستند اونا رو مختلط در نظر بگيريم يا حقيقي؟
سوال بعد:
 دو چندجمله ای تکین و تجزیه ناپذیر در
دو چندجمله ای تکین و تجزیه ناپذیر در
 هستند.اگرp,q دارای ریشه های
هستند.اگرp,q دارای ریشه های
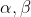 باشند که
باشند که
 نشان دهید چند جمله ای
نشان دهید چند جمله ای
 یک ریشه گویا دارد.
یک ریشه گویا دارد.
این سوال، سوال واقعا قشنگیه(البته به نظر من) و کلا دید من رو نسبت به چندجمله ای عوض کرد.:25:
 (من بعد از حل این سوال:4
(من بعد از حل این سوال:4
این سوال، سوال واقعا قشنگیه(البته به نظر من) و کلا دید من رو نسبت به چندجمله ای عوض کرد.:25:
- ارسال ها
- 331
- لایک ها
- 264
- امتیاز
- 0
پاسخ : ماراتن جبر (سطح پیشرفته)
از صورت سوال معلوم است که ضرایب چند جمله ای عضو اعداد گویا هستند. (q به معنای اعداد گویاست).
ولی دوستان اول سوال مربوط به بیشترین مقدار مجموع قددرمطلق ها رو حل کنید و بعد برید سراغ سوال بعدی.
اگر نیاز به راهنمایی بیشتر هست بگید تا راهنمایی کنم یا حل کنم. ممنون از لطف شما دوستان.
ما بايد تو اينگونه مسائل كه مشخص نكرده ضرايب چند جمله اي ها و ... عضو چه مجموعه اي هستند اونا رو مختلط در نظر بگيريم يا حقيقي؟
ولی دوستان اول سوال مربوط به بیشترین مقدار مجموع قددرمطلق ها رو حل کنید و بعد برید سراغ سوال بعدی.
اگر نیاز به راهنمایی بیشتر هست بگید تا راهنمایی کنم یا حل کنم. ممنون از لطف شما دوستان.
پاسخ : ماراتن جبر (سطح پیشرفته)
طبق نامساوی حسابی هندسی:

پس حالت تساوی رخ داده.به راحتی نتیجه میشه f(1)=1و تابع همانیه
---- دو نوشته به هم متصل شده است ----
سوال بعد:


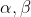


طبق نامساوی حسابی هندسی:
پس حالت تساوی رخ داده.به راحتی نتیجه میشه f(1)=1و تابع همانیه
---- دو نوشته به هم متصل شده است ----
سوال بعد:
دو چندجمله ای تکین و تجزیه ناپذیر در
(هم ضرایبشان گویاست و هم در مجمو عه ی اعداد گویا تجزیه ناپذیرند)هستند.اگرp,q دارای ریشه های
باشند که
نشان دهید چند جمله ای
یک ریشه گویا دارد.
پاسخ : ماراتن جبر (سطح پیشرفته)
سوال قبل با استفاده از نامساوی جایگشتی نیز نابود میشود !!!!
این سوال رو قبلا نگذاشته بودید ؟؟
طبق نامساوی حسابی هندسی:

پس حالت تساوی رخ داده.به راحتی نتیجه میشه f(1)=1و تابع همانیه
---- دو نوشته به هم متصل شده است ----
سوال بعد:


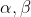


پس حالت تساوی رخ داده.به راحتی نتیجه میشه f(1)=1و تابع همانیه
---- دو نوشته به هم متصل شده است ----
سوال بعد:
دو چندجمله ای تکین و تجزیه ناپذیر در
(هم ضرایبشان گویاست و هم در مجمو عه ی اعداد گویا تجزیه ناپذیرند)هستند.اگرp,q دارای ریشه های
باشند که
نشان دهید چند جمله ای
یک ریشه گویا دارد.
این سوال رو قبلا نگذاشته بودید ؟؟
