ماراتن جبر (سطح پیشرفته)
پاسخ : ماراتن جبر (سطح پیشرفته)
الان يه سوال براي من پيش اومده اگه درجه ي (p(x يك باشه اون وقت اين چند جمله اي فقط يكي ريشه داره كه اون گوياست پس (q(x هم يه ريشه ي گويا داره و ما مي تونيم (q(x رو به دو چند جمله اي با ضرايب گويا تجزيه كنيم كه اين با فرض سوال در تناقضه.
سوال بعد:
 دو چندجمله ای تکین و تجزیه ناپذیر در
دو چندجمله ای تکین و تجزیه ناپذیر در
 هستند.اگرp,q دارای ریشه های
هستند.اگرp,q دارای ریشه های
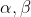 باشند که
باشند که
 نشان دهید چند جمله ای
نشان دهید چند جمله ای
 یک ریشه گویا دارد.
یک ریشه گویا دارد.
این سوال، سوال واقعا قشنگیه(البته به نظر من) و کلا دید من رو نسبت به چندجمله ای عوض کرد.:25:
 (من بعد از حل این سوال:4
(من بعد از حل این سوال:4
این سوال، سوال واقعا قشنگیه(البته به نظر من) و کلا دید من رو نسبت به چندجمله ای عوض کرد.:25:
پاسخ : ماراتن جبر (سطح پیشرفته)
(q(x رو نمیتونیم به دلخواه انتخاب کنیم.یعنی (p(x),q(x به ما داده شدن که شرایط مساله رو دارن.تو این حالتی که شما فرمودین برای این که شرایط برقرار باشه الزاما باید درجه q یک باشه.
این چیزی که پایین میگم هم برا اینه که بتونید بهتر رو مساله فکر کنید،البته این چیزهایی که میگم ممکنه دقیق نباشه و بر اساس چیزهایی که شنیدم و خوندمه
(استاد math اگه اشتباهی داشت بگید تصحیح کنم)
اگه برای عدد(حقیقی یا مختلط)
 یه چند جمله ای تکین با ضرایب گویا وجود داشته باشه که
یه چند جمله ای تکین با ضرایب گویا وجود داشته باشه که
 ریشه اون باشه بین این جور چند جمله ای ها چند جمله ای با کوچکترین درجه رو چندجمله ای مینیمال
ریشه اون باشه بین این جور چند جمله ای ها چند جمله ای با کوچکترین درجه رو چندجمله ای مینیمال
 میگیم(کلا ضرایب صحیح یا گویا بودنشون مهم نیست یعنی در واقع داریم یه عدد صحیح رو در چندجمله ای ضرب میکنیم مثلا میتونستیم بگیم چندجمله ای با ضرایب صحیح رو بگیرید که درجه آن از همه کمتر است و ب.م.م ضرایب آن 1 است)یکی از خواص چندجمله ای مینیمال اینه:
میگیم(کلا ضرایب صحیح یا گویا بودنشون مهم نیست یعنی در واقع داریم یه عدد صحیح رو در چندجمله ای ضرب میکنیم مثلا میتونستیم بگیم چندجمله ای با ضرایب صحیح رو بگیرید که درجه آن از همه کمتر است و ب.م.م ضرایب آن 1 است)یکی از خواص چندجمله ای مینیمال اینه:
اگه چندجمله مینیمال
 ،
،
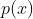 باشه اون وقت اگه برای یه چندجمله ای مثل q با ضرایب گویا،
باشه اون وقت اگه برای یه چندجمله ای مثل q با ضرایب گویا،
 اون وقت:
اون وقت:

حالا تو این مساله p,q چند جمله ای های مینیمال
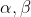 هستند.
هستند.
الان يه سوال براي من پيش اومده اگه درجه ي (p(x يك باشه اون وقت اين چند جمله اي فقط يكي ريشه داره كه اون گوياست پس (q(x هم يه ريشه ي گويا داره و ما مي تونيم (q(x رو به دو چند جمله اي با ضرايب گويا تجزيه كنيم كه اين با فرض سوال در تناقضه.
این چیزی که پایین میگم هم برا اینه که بتونید بهتر رو مساله فکر کنید،البته این چیزهایی که میگم ممکنه دقیق نباشه و بر اساس چیزهایی که شنیدم و خوندمه
(استاد math اگه اشتباهی داشت بگید تصحیح کنم)
اگه برای عدد(حقیقی یا مختلط)
اگه چندجمله مینیمال
حالا تو این مساله p,q چند جمله ای های مینیمال
آخرین ویرایش توسط مدیر
پاسخ : ماراتن جبر (سطح پیشرفته)
این هم ادامه راه حل:
 ریشه
ریشه
 است و چون
است و چون
 ضرایب این چند جمله ای گویاست.پس طبق گفته های بالا
ضرایب این چند جمله ای گویاست.پس طبق گفته های بالا
 .به طریق مشابه
.به طریق مشابه

با کمی بررسی میتوان فهمید که
 .پس
.پس
 .
.
سوال بعد:
همه چند جمله ای های باضرایب حقیقی رو پیدا کنید که اگر
 صحیح باشد، a هم صحیح باشد.(برای هر a)هر کی حل کرد سوال بعد رو بزاره لطفا:87:
صحیح باشد، a هم صحیح باشد.(برای هر a)هر کی حل کرد سوال بعد رو بزاره لطفا:87:
این هم ادامه راه حل:
با کمی بررسی میتوان فهمید که
سوال بعد:
همه چند جمله ای های باضرایب حقیقی رو پیدا کنید که اگر
- ارسال ها
- 331
- لایک ها
- 264
- امتیاز
- 0
پاسخ : ماراتن جبر (سطح پیشرفته)
جواب سوال:
http://www.artofproblemsolving.com/Forum/viewtopic.php?t=392444
سوال بعد رو هم یکی از دوستان بزاره:65:
سوال بعد:
همه چند جمله ای های باضرایب حقیقی رو پیدا کنید که اگر
 صحیح باشد، a هم صحیح باشد.(برای هر a)هر کی حل کرد سوال بعد رو بزاره لطفا:87:
صحیح باشد، a هم صحیح باشد.(برای هر a)هر کی حل کرد سوال بعد رو بزاره لطفا:87:
همه چند جمله ای های باضرایب حقیقی رو پیدا کنید که اگر
http://www.artofproblemsolving.com/Forum/viewtopic.php?t=392444
سوال بعد رو هم یکی از دوستان بزاره:65:
پاسخ : ماراتن جبر (سطح پیشرفته)
ابتدا x=y=0 رو قرار ميديم كه بدست مياد:
(1)

و با قرار دادن (f(x به جاي y بدست مياد:
(2)

حالا x=0 رو در رابطه ي بالا جايگذاري مي كنيم و با توجه به (1) داريم:

با قرار دادن x به جاي y و صفر به جاي x در رابطه ي اصلي مسئله داريم:

با قرار دادن اين رابطه در (2) بدست مياد:

كه در صورت سوال هم صدق مي كنه.
سوال بعد:
تمام توابع
 بيابيد به طوريكه براي هر
بيابيد به طوريكه براي هر
 داشته باشيم:
داشته باشيم:

(1)
و با قرار دادن (f(x به جاي y بدست مياد:
(2)
حالا x=0 رو در رابطه ي بالا جايگذاري مي كنيم و با توجه به (1) داريم:
با قرار دادن x به جاي y و صفر به جاي x در رابطه ي اصلي مسئله داريم:
با قرار دادن اين رابطه در (2) بدست مياد:
كه در صورت سوال هم صدق مي كنه.
سوال بعد:
تمام توابع
آخرین ویرایش توسط مدیر
پاسخ : ماراتن جبر (سطح پیشرفته)
فرض کنید



حالا با توجه به این که
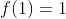 داریم :
داریم :

 حالا با توجه به یک به یک بودن تابع داریم :
حالا با توجه به یک به یک بودن تابع داریم :

به این رابطه میگیم رابطه ی I.
داریم :

که با چند بار استفاده از رابطه ی I به دست می آد :

از طرفی :
 پس :
پس :
 که با دلخواه بودن
که با دلخواه بودن
 در تناقضه. پس چنین تابعی وجود نداره ...
در تناقضه. پس چنین تابعی وجود نداره ...
امیدوارم جوب نزده باشم !
(خودمونیم، پدرم در اومد! ببخشید طولانی شد)
راستی سوال ندارم. یه نفر زحمتشو بکشه ...
فرض کنید
برابر با
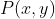 باشه.
باشه.
داریم :
داریم :
که به وضوح نتیجه می ده که تابع یک به یکه.
داریم :
امیدوارم جوب نزده باشم !
(خودمونیم، پدرم در اومد! ببخشید طولانی شد)
راستی سوال ندارم. یه نفر زحمتشو بکشه ...
آخرین ویرایش توسط مدیر
پاسخ : ماراتن جبر (سطح پیشرفته)
لینک(به قول استاد nima1376:204 :
:
AoPS Forum - f(f(x)^2*y)=x^3f*(xy) • Art of Problem Solving
راه حل آخریه هم مال ایشونه...
---- دو نوشته به هم متصل شده است ----
سوال بعد:
همه توابع
 را بیابید به طوری که:
را بیابید به طوری که:


سوال بعد:
تمام توابع
 بيابيد به طوريكه براي هر
بيابيد به طوريكه براي هر
 داشته باشيم:
داشته باشيم:

تمام توابع
AoPS Forum - f(f(x)^2*y)=x^3f*(xy) • Art of Problem Solving
راه حل آخریه هم مال ایشونه...
---- دو نوشته به هم متصل شده است ----
سوال بعد:
همه توابع
آخرین ویرایش توسط مدیر
پاسخ : ماراتن جبر (سطح پیشرفته)
ابتدا ثابت مي كنيم اين تابع پوشاست. رابطه ي اصلي مسئله را (1) نامگذاري مي كنيم. در رابطه ي (1)
 را جايگذاري مي كنيم كه نشان مي دهد تابع پوشاست.
را جايگذاري مي كنيم كه نشان مي دهد تابع پوشاست.
پس aاي موجود است كه داشته باشيم f(a)=0. در رابطه ي (1) x=y=0 را جايگذاري مي كنيم كه بدست مياد
 و با گذاشتن x=a
و با گذاشتن x=a
و y=0 در رابطه ي (1) بدست مياد a=0 پس f(0)=0 است.y=0 را در رابطه ي (1) جايگذاري مي كنيم پس داريم:

و با جايگذاري x=0 و y=x در رابطه ي (1) داريم:
 با جايگذاري دو رابطه ي اخير در (1) بدست مياد:
با جايگذاري دو رابطه ي اخير در (1) بدست مياد:

حالا داريم:
 پس (x+f(x هم پوشاست و به ازاي هر
پس (x+f(x هم پوشاست و به ازاي هر
 داريم:
داريم:
 و مي توان به راحتي ثابت كرد كه
و مي توان به راحتي ثابت كرد كه
 با جايگذاري اين رابطه در (1) بدست مياد C=1 پس داريم
با جايگذاري اين رابطه در (1) بدست مياد C=1 پس داريم

سوال بعد:
تمام توابع
 را بيابيد به طوريكه براي هر
را بيابيد به طوريكه براي هر
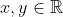 داشته باشيم:
داشته باشيم:

سوال بعد:
همه توابع
 را بیابید به طوری که:
را بیابید به طوری که:


همه توابع
پس aاي موجود است كه داشته باشيم f(a)=0. در رابطه ي (1) x=y=0 را جايگذاري مي كنيم كه بدست مياد
و y=0 در رابطه ي (1) بدست مياد a=0 پس f(0)=0 است.y=0 را در رابطه ي (1) جايگذاري مي كنيم پس داريم:
و با جايگذاري x=0 و y=x در رابطه ي (1) داريم:
حالا داريم:
سوال بعد:
تمام توابع
آخرین ویرایش توسط مدیر
پاسخ : ماراتن جبر (سطح پیشرفته)
فرض کنید (p(x,y رابطه ی اصلی مساله باشه،در این صورت:
(1)

(2)

با جایگذاری اولی در دومی بدست میاد:

با جایگذاری این در رابطه ی اول بدست میاد:

حالا اگه اینا رو توی رابطه اصلی مساله بزاریم بدست میاد a=0 پس f,g این شکلی اند:
 .
.
---- دو نوشته به هم متصل شده است ----
اگه درسته این هم سوال بعد:
همه ی چند جمله ای ها با ضرایب حقیقی مانند (p(x را بیابید به طوری که:

سوال بعد:
تمام توابع
 را بيابيد به طوريكه براي هر
را بيابيد به طوريكه براي هر
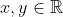 داشته باشيم:
داشته باشيم:

تمام توابع
(1)
(2)
با جایگذاری اولی در دومی بدست میاد:
با جایگذاری این در رابطه ی اول بدست میاد:
حالا اگه اینا رو توی رابطه اصلی مساله بزاریم بدست میاد a=0 پس f,g این شکلی اند:
---- دو نوشته به هم متصل شده است ----
اگه درسته این هم سوال بعد:
همه ی چند جمله ای ها با ضرایب حقیقی مانند (p(x را بیابید به طوری که:
آخرین ویرایش توسط مدیر



