ماراتن نظریه ی اعداد (سطح پیشرفته)
- ارسال ها
- 1,351
- لایک ها
- 1,322
- امتیاز
- 113
پاسخ : ماراتن نظریه ی اعداد (سطح پیشرفته)
ابتدا ثابت میکنیم که تو این دنباله یه عدد مضرب 4 هست.
بعد با توجه به این که :

پس برای این که عدد توان دو تولید کنیم کافیه:

در این صورت حتما یک m وجود دارد . :4:
اهم اهم با اجازه من سوالو میزازم
دنباله ی a1,a2,a3,...,an,...از اعداد طبیعی مفروض استبه طوری که anبر 5 بخش پذیر نیستوبرای هر nداریم:an+1=an+bnکهbnآخرین رقم (رقم یکان)anاست.ثابت کنید این دنباله مشتمل بر تعداد نا متناهی توان 2 است.
دنباله ی a1,a2,a3,...,an,...از اعداد طبیعی مفروض استبه طوری که anبر 5 بخش پذیر نیستوبرای هر nداریم:an+1=an+bnکهbnآخرین رقم (رقم یکان)anاست.ثابت کنید این دنباله مشتمل بر تعداد نا متناهی توان 2 است.
بعد با توجه به این که :
پس برای این که عدد توان دو تولید کنیم کافیه:
آخرین ویرایش توسط مدیر
پاسخ : ماراتن نظریه ی اعداد (سطح پیشرفته)
جواب مساله
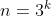 میباشد چون به ازای
میباشد چون به ازای
 وجود ندارد به طوری که :
وجود ندارد به طوری که :
 اثبات هم با برهان خلف است :
اثبات هم با برهان خلف است :
 اما :
اما :
 پس
پس
 که به وضوح غیرممکنه.
که به وضوح غیرممکنه.
به ازای N های دیگه مساله جواب نداره. اگه دوستی راه حل این قسمت رو میخواد بگه بنویسم.
* در ضمن راهنمایی که برای سوال خودم گذاشته بودم چیزی کم از راه حل نداشت. نمیدونم شما چطور میگید سوال به مدت طولانی حل نشده!*
:223:
چون سوال قبل به مدت زیادی حل نشده باقی مونده من سوال بعدو میذارم:
همه ی اعداد طبیعی
 را بیابید که برای هر
را بیابید که برای هر
 ی صحیح وجود داشته باشد
ی صحیح وجود داشته باشد
 ای که
ای که
 .
.
همه ی اعداد طبیعی
به ازای N های دیگه مساله جواب نداره. اگه دوستی راه حل این قسمت رو میخواد بگه بنویسم.
* در ضمن راهنمایی که برای سوال خودم گذاشته بودم چیزی کم از راه حل نداشت. نمیدونم شما چطور میگید سوال به مدت طولانی حل نشده!*
:223:
آخرین ویرایش توسط مدیر
پاسخ : ماراتن نظریه ی اعداد (سطح پیشرفته)
منظورم این سوال بود:
که شرت لیست 2007 هست. سوال بعد:
ثابت کنید بی نهایت n صحیح وجود دارد که
 خالی از مربع باشد.
خالی از مربع باشد.
جواب مساله
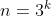 میباشد چون به ازای
میباشد چون به ازای
 وجود ندارد به طوری که :
وجود ندارد به طوری که :
 اثبات هم با برهان خلف است :
اثبات هم با برهان خلف است :
 اما :
اما :
 پس
پس
 که به وضوح غیرممکنه.
که به وضوح غیرممکنه.
به ازای N های دیگه مساله جواب نداره. اگه دوستی راه حل این قسمت رو میخواد بگه بنویسم.
* در ضمن راهنمایی که برای سوال خودم گذاشته بودم چیزی کم از راه حل نداشت. نمیدونم شما چطور میگید سوال به مدت طولانی حل نشده!*
:223:
به ازای N های دیگه مساله جواب نداره. اگه دوستی راه حل این قسمت رو میخواد بگه بنویسم.
* در ضمن راهنمایی که برای سوال خودم گذاشته بودم چیزی کم از راه حل نداشت. نمیدونم شما چطور میگید سوال به مدت طولانی حل نشده!*
:223:
Kتمام توابع
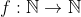 به طوری که برای هر
به طوری که برای هر

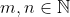 و هر عدد اول
و هر عدد اول
 ،
،
 اگر و فقط اگر
اگر و فقط اگر
 .
.
ثابت کنید بی نهایت n صحیح وجود دارد که
- ارسال ها
- 159
- لایک ها
- 282
- امتیاز
- 0
پاسخ : ماراتن نظریه ی اعداد (سطح پیشرفته)
لم :

اثبات:

حال فرض کنید
 اول باشد، دقت کنید که
اول باشد، دقت کنید که
 حال اگر هر دو همزمان رخ دهند،
حال اگر هر دو همزمان رخ دهند،
 اما دقت کنید که
اما دقت کنید که
 پس
پس
 پس
پس
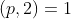 پس
پس
 که تناقض است. پس دقیقا یکی از
که تناقض است. پس دقیقا یکی از
 و
و
 رخ میدهد، پس
رخ میدهد، پس
 . از طرفی بدیهتا
. از طرفی بدیهتا
 زیرا
زیرا
 .
.
حال میخواهیم ببینیم برای یک
 ثابت، چند عدد مانند
ثابت، چند عدد مانند
 وجود دارد که
وجود دارد که
 و
و
 خالی از مربع نیست. در حقیقت، میبینیم که چند
خالی از مربع نیست. در حقیقت، میبینیم که چند
 هستند که
هستند که
 بر یک
بر یک
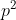 - که
- که
 اول و ثابت است - بخش پذیر است، سپس تعداد کل اعداد با این خاصیت، طبق اصل شمول و عدم شمول كمتر مساوي جمع این اعداد برای
اول و ثابت است - بخش پذیر است، سپس تعداد کل اعداد با این خاصیت، طبق اصل شمول و عدم شمول كمتر مساوي جمع این اعداد برای
 های مختلف است.
های مختلف است.
لم :
اثبات:
حال فرض کنید
حال میخواهیم ببینیم برای یک
دقت کنید که این عدد برای یک
 که ثابت است یا صفر است - هیچ
که ثابت است یا صفر است - هیچ
 وجود ندارد که
وجود ندارد که
 مانند حالت 2 و 3- یا حداکثر
مانند حالت 2 و 3- یا حداکثر
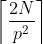 است زیرا برابر با تعداد اعدادی است که از
است زیرا برابر با تعداد اعدادی است که از
 کمتر مساویند و به پیمانه
کمتر مساویند و به پیمانه
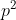 با مثبت یا منفی یک عدد ثابت همنهشتند. حال بدیهتا همه
با مثبت یا منفی یک عدد ثابت همنهشتند. حال بدیهتا همه
 هايي كه براي آنها
هايي كه براي آنها
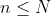 وجود دارد بطوري كه
وجود دارد بطوري كه
 ،كمتر يا مساوي
،كمتر يا مساوي
 هستند. بنابرين كافيست
هستند. بنابرين كافيست
 را بيابيم كه حداكثر تعداد اعدادي كه در خاصيت ما صدق نميكنند را بيابيم. دقت كنيد كه اگر
را بيابيم كه حداكثر تعداد اعدادي كه در خاصيت ما صدق نميكنند را بيابيم. دقت كنيد كه اگر
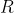 تعداد اعداد اول نابیشتر از
تعداد اعداد اول نابیشتر از
 باشد آنگاه
باشد آنگاه
 و
و

حال دقت کنید که همه اعداد به غیر از 2و3و5 به پیمانه 30 همنهشت یکی از اعداد
 هستند. پس فرض کنید که
هستند. پس فرض کنید که
 در این صورت
در این صورت
 پس
پس
 یعنی تعداد اعدادی که مناسب ما نیستند حداکثر
یعنی تعداد اعدادی که مناسب ما نیستند حداکثر
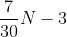 است، پس تعداد اعدادی که مناسب ما هستند حداقل برابر است با
است، پس تعداد اعدادی که مناسب ما هستند حداقل برابر است با
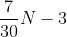 که با زیاد شدن
که با زیاد شدن
 به هر اندازه زیاد می شود. پس تعداد اعدادی که مناسب ما هستند به هر اندازه زیاد میشود، پس بینهایت تا از این اعداد داریم.
به هر اندازه زیاد می شود. پس تعداد اعدادی که مناسب ما هستند به هر اندازه زیاد میشود، پس بینهایت تا از این اعداد داریم.
سوال بعد:
همه چند جمله ای های
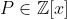 را بیابید که برای هر
را بیابید که برای هر
 ، وجود داشته باشد
، وجود داشته باشد
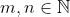 که
که

حال دقت کنید که همه اعداد به غیر از 2و3و5 به پیمانه 30 همنهشت یکی از اعداد
سوال بعد:
همه چند جمله ای های
آخرین ویرایش توسط مدیر
- ارسال ها
- 935
- لایک ها
- 1,654
- امتیاز
- 93
پاسخ : ماراتن نظریه ی اعداد (سطح پیشرفته)
در اثنای دینی خوندن اونم تا دیروقت ، تصمیم گرفتم رو این سوال فکر کنم !!

الان اگه p,q هردو بخوان فرد باشند یعنی طرف راست مطلقا فرد خواهد بود ( درصورت 2 نبودن r ) و طرف چپ زوج پس بلافاصله نتیجه میگیریم که r=2

پس :

پس :

حالا داریم :

پس داریم :

که می بینیم از جایی به بعد غلطه ( ببخشید الان نصفه شبه حوصله ندارم چک کنم اما چون درجه راست 3 و چپ 2 هست معلومه از جایی به بعد بهم میخوره )
پس حالتی که p=q باشه میمونه که در اون صورت p^3 = 2q^2 که یعنی p=q=2 .
پس یه مجموعه جواب : (2,2,r) بقیش طبق رابطه بالا میشه !
خداکنه جوپ نداشته باشه !!
یه سوال قشنگ:
همه ی اعداد اول دو به دو متمایز
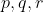 را بیابید که
را بیابید که
 .
.
همه ی اعداد اول دو به دو متمایز
حالتی که p,q با هم برابر باشند رو فعلا کنار میذاریم و فرض میکنیم متمایزند و از اینجا به راحتی بدست میاد q از p بزرگ تر هستش . الان اگه p,q هردو بخوان فرد باشند یعنی طرف راست مطلقا فرد خواهد بود ( درصورت 2 نبودن r ) و طرف چپ زوج پس بلافاصله نتیجه میگیریم که r=2
پس :
پس :
حالا داریم :
پس داریم :
که می بینیم از جایی به بعد غلطه ( ببخشید الان نصفه شبه حوصله ندارم چک کنم اما چون درجه راست 3 و چپ 2 هست معلومه از جایی به بعد بهم میخوره )
پس حالتی که p=q باشه میمونه که در اون صورت p^3 = 2q^2 که یعنی p=q=2 .
پس یه مجموعه جواب : (2,2,r) بقیش طبق رابطه بالا میشه !
خداکنه جوپ نداشته باشه !!
- ارسال ها
- 1,351
- لایک ها
- 1,322
- امتیاز
- 113
پاسخ : ماراتن نظریه ی اعداد (سطح پیشرفته)
خوب رو سوال گفته دو به دو متمایز(انگار دینی خوندن رو دقتتون تاثیر گزاشته!!!)
پس ینی جواب نداریم دیگه.
در اثنای دینی خوندن اونم تا دیروقت ، تصمیم گرفتم رو این سوال فکر کنم !!
 حالتی که p,q با هم برابر باشند رو فعلا کنار میذاریم و فرض میکنیم متمایزند و از اینجا به راحتی بدست میاد q از p بزرگ تر هستش .
حالتی که p,q با هم برابر باشند رو فعلا کنار میذاریم و فرض میکنیم متمایزند و از اینجا به راحتی بدست میاد q از p بزرگ تر هستش .
الان اگه p,q هردو بخوان فرد باشند یعنی طرف راست مطلقا فرد خواهد بود ( درصورت 2 نبودن r ) و طرف چپ زوج پس بلافاصله نتیجه میگیریم که r=2

پس :

پس :

حالا داریم :

پس داریم :

که می بینیم از جایی به بعد غلطه ( ببخشید الان نصفه شبه حوصله ندارم چک کنم اما چون درجه راست 3 و چپ 2 هست معلومه از جایی به بعد بهم میخوره )
پس حالتی که p=q باشه میمونه که در اون صورت p^3 = 2q^2 که یعنی p=q=2 .
پس یه مجموعه جواب : (2,2,r) بقیش طبق رابطه بالا میشه !
خداکنه جوپ نداشته باشه !!
الان اگه p,q هردو بخوان فرد باشند یعنی طرف راست مطلقا فرد خواهد بود ( درصورت 2 نبودن r ) و طرف چپ زوج پس بلافاصله نتیجه میگیریم که r=2
پس :
پس :
حالا داریم :
پس داریم :
که می بینیم از جایی به بعد غلطه ( ببخشید الان نصفه شبه حوصله ندارم چک کنم اما چون درجه راست 3 و چپ 2 هست معلومه از جایی به بعد بهم میخوره )
پس حالتی که p=q باشه میمونه که در اون صورت p^3 = 2q^2 که یعنی p=q=2 .
پس یه مجموعه جواب : (2,2,r) بقیش طبق رابطه بالا میشه !
خداکنه جوپ نداشته باشه !!
پس ینی جواب نداریم دیگه.
پاسخ : ماراتن نظریه ی اعداد (سطح پیشرفته)
راه حلتون درسته و اگه اون نامساوي رو هم چك كنيد جواب
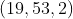 بدست مياد ولي اون نامساوي هايي كه نوشتين همشون بايد حالت تساوي هم داشته باشن چون اگه اينجوري نباشه يه جوابي كه سوال داره بدست نمياد.
بدست مياد ولي اون نامساوي هايي كه نوشتين همشون بايد حالت تساوي هم داشته باشن چون اگه اينجوري نباشه يه جوابي كه سوال داره بدست نمياد.
سوال بعد:
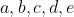 اعدادي صحيح و مثبت هستند به طوريكه
اعدادي صحيح و مثبت هستند به طوريكه
 ثابت كنيد
ثابت كنيد
 عددي مركب است.
عددي مركب است.
در اثنای دینی خوندن اونم تا دیروقت ، تصمیم گرفتم رو این سوال فکر کنم !!
 حالتی که p,q با هم برابر باشند رو فعلا کنار میذاریم و فرض میکنیم متمایزند و از اینجا به راحتی بدست میاد q از p بزرگ تر هستش .
حالتی که p,q با هم برابر باشند رو فعلا کنار میذاریم و فرض میکنیم متمایزند و از اینجا به راحتی بدست میاد q از p بزرگ تر هستش .
الان اگه p,q هردو بخوان فرد باشند یعنی طرف راست مطلقا فرد خواهد بود ( درصورت 2 نبودن r ) و طرف چپ زوج پس بلافاصله نتیجه میگیریم که r=2

پس :

پس :

حالا داریم :

پس داریم :

که می بینیم از جایی به بعد غلطه ( ببخشید الان نصفه شبه حوصله ندارم چک کنم اما چون درجه راست 3 و چپ 2 هست معلومه از جایی به بعد بهم میخوره )
پس حالتی که p=q باشه میمونه که در اون صورت p^3 = 2q^2 که یعنی p=q=2 .
پس یه مجموعه جواب : (2,2,r) بقیش طبق رابطه بالا میشه !
خداکنه جوپ نداشته باشه !!
الان اگه p,q هردو بخوان فرد باشند یعنی طرف راست مطلقا فرد خواهد بود ( درصورت 2 نبودن r ) و طرف چپ زوج پس بلافاصله نتیجه میگیریم که r=2
پس :
پس :
حالا داریم :
پس داریم :
که می بینیم از جایی به بعد غلطه ( ببخشید الان نصفه شبه حوصله ندارم چک کنم اما چون درجه راست 3 و چپ 2 هست معلومه از جایی به بعد بهم میخوره )
پس حالتی که p=q باشه میمونه که در اون صورت p^3 = 2q^2 که یعنی p=q=2 .
پس یه مجموعه جواب : (2,2,r) بقیش طبق رابطه بالا میشه !
خداکنه جوپ نداشته باشه !!
سوال بعد:
