پاسخ : ماراتن نظریه ی اعداد (سطح پیشرفته)
سوال بعد:
همه چند جمله ای های
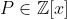 را بیابید که برای هر
را بیابید که برای هر
 ، وجود داشته باشد
، وجود داشته باشد
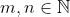 که
که

برای هر عدد اول و دلخواه مثل q داریم:
 اگر درجه f بیشتر از 1 باشه اون وقت مقادیری که مشتق اون به ازای اعداد طبیعی میگیره بینهایت عامل اول دارن.چون درجه مشتقش حداقل 1 میشه.مثلا فرض کنید :
اگر درجه f بیشتر از 1 باشه اون وقت مقادیری که مشتق اون به ازای اعداد طبیعی میگیره بینهایت عامل اول دارن.چون درجه مشتقش حداقل 1 میشه.مثلا فرض کنید :
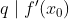
 این یعنی
این یعنی
 و همچنین
و همچنین
 به پیمانه q^2 همنهشت نیستند.حالا نشون میدیم که این شرط سوال رو نقض میکنه.
به پیمانه q^2 همنهشت نیستند.حالا نشون میدیم که این شرط سوال رو نقض میکنه.
اگر
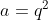 و b بین 1 تا q^2 تغییر کنه،نتیجه میشه که
و b بین 1 تا q^2 تغییر کنه،نتیجه میشه که
 به ازای
به ازای
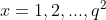 همه باقیمانده های ممکن رو به پیمانه q^2 میده.یعنی:
همه باقیمانده های ممکن رو به پیمانه q^2 میده.یعنی:
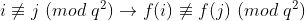
اما برای
 چنین چیزی برقرار نیست.پس درجه f حداکثر 1 هه.این جا به بعدش هم زیاد سخت نیست.درسته؟
چنین چیزی برقرار نیست.پس درجه f حداکثر 1 هه.این جا به بعدش هم زیاد سخت نیست.درسته؟
---- دو نوشته به هم متصل شده است ----
http://artofproblemsolving.com/community/c5h1083472p4774020
سوال بعد:
همه چند جمله ای های
اگر
---- دو نوشته به هم متصل شده است ----
راه حلتون درسته و اگه اون نامساوي رو هم چك كنيد جواب
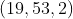 بدست مياد ولي اون نامساوي هايي كه نوشتين همشون بايد حالت تساوي هم داشته باشن چون اگه اينجوري نباشه يه جوابي كه سوال داره بدست نمياد.
بدست مياد ولي اون نامساوي هايي كه نوشتين همشون بايد حالت تساوي هم داشته باشن چون اگه اينجوري نباشه يه جوابي كه سوال داره بدست نمياد.
سوال بعد:
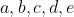 اعدادي صحيح و مثبت هستند به طوريكه
اعدادي صحيح و مثبت هستند به طوريكه
 ثابت كنيد
ثابت كنيد
 عددي مركب است.
عددي مركب است.
سوال بعد:
