ماراتن هندسه
- ارسال ها
- 46
- لایک ها
- 0
- امتیاز
- 0
سلام
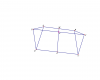
برای اثبات حکم ثابت میکنیم K مرکز ارتفاعی مثلث AMC است
وسط KC را X میگیریم
چون KPC متساوی الساقین است پس PX بر KC است
از طرفی MX موازی و نصف BC است
یعنی AMXP متوازی الاضلاع است
چون داشتیم PX بر KC عمود است پس AM نیز بر KC عمود است
به طریق مشابه تعامد های دیگر نیز اثبات می شود
حالا که K مرکز ارتفاعی AMC شد حکم مساله بدیهی می شود
برای اثبات حکم ثابت میکنیم K مرکز ارتفاعی مثلث AMC است
وسط KC را X میگیریم
چون KPC متساوی الساقین است پس PX بر KC است
از طرفی MX موازی و نصف BC است
یعنی AMXP متوازی الاضلاع است
چون داشتیم PX بر KC عمود است پس AM نیز بر KC عمود است
به طریق مشابه تعامد های دیگر نیز اثبات می شود
حالا که K مرکز ارتفاعی AMC شد حکم مساله بدیهی می شود
- ارسال ها
- 335
- لایک ها
- 8
- امتیاز
- 0
باید به جای AB=CD قرار دهی AD=BC
لم : اگر دو مثلث ABC , DEF داشته باشیم و M وسط AD و N وسط BE و P وسط CF باشد و اگر S[SUB]1[/SUB] مساحت (البته جهت دار) ABC و S[SUB]2[/SUB]
مساحت DEF باشد(البته جهت دار) و S[SUB]3[/SUB] مساحت MNP باشد آنگاه : 2S[SUB]3[/SUB]=S[SUB]1[/SUB]+S[SUB]2[/SUB] (اثباتش هم سخت نیست یه راه حلش ضرب خارجی
بردار هاست و یه راه حل هم استفاده از مختصات است ولی فکر میکنم راه حل آسون تر هم داشته باشه)
حال با استفاده از این لم و این که دو مثلث BYC و AXD همنهشتند و مساحت آنها قرینه است بدست میاید مساحت MNP صفر است یعنی
M,N,P همخطند.
لم : اگر دو مثلث ABC , DEF داشته باشیم و M وسط AD و N وسط BE و P وسط CF باشد و اگر S[SUB]1[/SUB] مساحت (البته جهت دار) ABC و S[SUB]2[/SUB]
مساحت DEF باشد(البته جهت دار) و S[SUB]3[/SUB] مساحت MNP باشد آنگاه : 2S[SUB]3[/SUB]=S[SUB]1[/SUB]+S[SUB]2[/SUB] (اثباتش هم سخت نیست یه راه حلش ضرب خارجی
بردار هاست و یه راه حل هم استفاده از مختصات است ولی فکر میکنم راه حل آسون تر هم داشته باشه)
حال با استفاده از این لم و این که دو مثلث BYC و AXD همنهشتند و مساحت آنها قرینه است بدست میاید مساحت MNP صفر است یعنی
M,N,P همخطند.
- ارسال ها
- 335
- لایک ها
- 8
- امتیاز
- 0
seifi_seifi گفت
مساله ی بعدی :
چهار ضلعی محاطی ABCD مفروض است. دایره ای با مرکزی روی CD بر AB , BC , AD مماس است.
ثابت کنید AD+BC=CD
چهار ضلعی محاطی ABCD مفروض است. دایره ای با مرکزی روی CD بر AB , BC , AD مماس است.
ثابت کنید AD+BC=CD
مرکز این دایره را O میگیریم. پس BO و AO نیمساز زاویه های ABC و BAD هستند.حال نقطه ی M را روی BC طوری انتخاب میکنیم که
AD=DM.حال داریم : DAM=(180-D)/2=B/2=OBA (زاویه) پس چهار ضلعی BOMA محاطی است پس :
OMB=OAB=OAD=OAM+DAM=OBM+AMD=OBM+OBA=OBM+OBC=CBM (زاویه)
پس OMB=CBM (زاویه) پس CB=CM پس AD+CB=DM+MC=DC
سوال بعدی رو یکی بذاره... .
نذارین این ماراتن بخوابه ...

برای سوال قبلی کافیه برید راه حل در صفحهٔ ۲۲۶ کتاب آلتشیر کورت رو بخونید...
اگر هم خیلی لازم باشه راه حلشو خلاصه میگم...
بریم سراغ سوال بعدی :
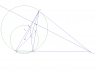
مطابق شکل فرض کنید که ABC یک مثلث است .و نقط D روی BC قرار داره . فرض کنید که دایرهٔ دلخواه (K) که از B،D میگذرد AB،AD رو در E,F قطع کنه.حالا ED و BF همدیگر را در G قطع میکنند.وسط AG را M بنامید.ثابت کنید که CM بر AK عمود است اگر و فقط اگر زاویهٔ CAD
برابر با زاویهٔ ABC باشد.
(احساس میکنم سوال سختی باشه، البته میدونم شما قادرید حلش کنید ... اگر سطحش بالاتر از حد معمول به من بگید تا عوضش کنم یا راهنمایی کنم )


برای سوال قبلی کافیه برید راه حل در صفحهٔ ۲۲۶ کتاب آلتشیر کورت رو بخونید...
اگر هم خیلی لازم باشه راه حلشو خلاصه میگم...
بریم سراغ سوال بعدی :
مطابق شکل فرض کنید که ABC یک مثلث است .و نقط D روی BC قرار داره . فرض کنید که دایرهٔ دلخواه (K) که از B،D میگذرد AB،AD رو در E,F قطع کنه.حالا ED و BF همدیگر را در G قطع میکنند.وسط AG را M بنامید.ثابت کنید که CM بر AK عمود است اگر و فقط اگر زاویهٔ CAD
برابر با زاویهٔ ABC باشد.
(احساس میکنم سوال سختی باشه، البته میدونم شما قادرید حلش کنید ... اگر سطحش بالاتر از حد معمول به من بگید تا عوضش کنم یا راهنمایی کنم )

پیوست ها
-
42 کیلوبایت بازدیدها 176
- ارسال ها
- 335
- لایک ها
- 8
- امتیاز
- 0
دستت درد نکنه سوال خیلی خیلی قشنگی بود .

راه حل :
ابتدا نقطه ی A را یک دایره به شعاع 0 در نظر میگیریم.حال ابتدا ثابت میکنیم اگر ABC=CAD آنگاه CM بر AK عمود است.
اگر ABC=CAD باشد آنگاه دایره محیطی ABD بر AC مماس است.پس خط AC محور اصلی دایره محیطی ABD و نقطه ی A است و چون
BD هم محور اصلی دایره ی K و دایره ی محیطی ABD است پس محور اصلی A و دایره ی K از C میگذرد و بر AK عمود است.یعنی باید ثابت
کنیم M روی محور اصلی دایره ی K و A قرار دارد.حال از A دو مماس AP,AQ بر دایره ی K رسم میکنیم و محور اصلی A و دایره ی K خطی
است که از وسط AP,AQ میگذرد و باید ثابت کنیم که M هم روی این خط است و چون M وسط AG است پس باید ثابت کنیم که G روی PQ قرار دارد(یک تجانس با نسبت 2 و مرکز A ) که این هم ساده است.(ثابت کنید مکان هندسی محل بر خورد BF , DE با تغییر
خطهای AB,AD خط PQ است.)
قسمت دیگر : حال میدانیم که M روی محور اصلی A و دایره ی K قرار دارد. و چون CM بر AK عمود است و C روی محور اصلی دایره ی
محیطی ABD و دایره ی K قرار دارد پس C روی محور اصلی A و دایره ی محیطی ABD نیز قرار دارد پس مماس بر دایره ی محیطی ABD در A
از C میگذرد.پس AC بر دایره ی محیطی ABD مماس است پس ABC=CAD
و اثبات کامل شد.... .


راه حل :
ابتدا نقطه ی A را یک دایره به شعاع 0 در نظر میگیریم.حال ابتدا ثابت میکنیم اگر ABC=CAD آنگاه CM بر AK عمود است.
اگر ABC=CAD باشد آنگاه دایره محیطی ABD بر AC مماس است.پس خط AC محور اصلی دایره محیطی ABD و نقطه ی A است و چون
BD هم محور اصلی دایره ی K و دایره ی محیطی ABD است پس محور اصلی A و دایره ی K از C میگذرد و بر AK عمود است.یعنی باید ثابت
کنیم M روی محور اصلی دایره ی K و A قرار دارد.حال از A دو مماس AP,AQ بر دایره ی K رسم میکنیم و محور اصلی A و دایره ی K خطی
است که از وسط AP,AQ میگذرد و باید ثابت کنیم که M هم روی این خط است و چون M وسط AG است پس باید ثابت کنیم که G روی PQ قرار دارد(یک تجانس با نسبت 2 و مرکز A ) که این هم ساده است.(ثابت کنید مکان هندسی محل بر خورد BF , DE با تغییر
خطهای AB,AD خط PQ است.)
قسمت دیگر : حال میدانیم که M روی محور اصلی A و دایره ی K قرار دارد. و چون CM بر AK عمود است و C روی محور اصلی دایره ی
محیطی ABD و دایره ی K قرار دارد پس C روی محور اصلی A و دایره ی محیطی ABD نیز قرار دارد پس مماس بر دایره ی محیطی ABD در A
از C میگذرد.پس AC بر دایره ی محیطی ABD مماس است پس ABC=CAD
و اثبات کامل شد.... .

- ارسال ها
- 2,239
- لایک ها
- 166
- امتیاز
- 0
seifi_seifi گفت
معمولا سوال هایی رو که هر کی میزاره دو تا هدف داره : 1- خودش حل نکرده 2-یا خیلی قشنگ و جدیده که میخواد دیگران هم استفاده کنند.
من هر چی فکر میکنم این سوال جزو هیچ کدوم از این دوتا هدف نمیتونه باشه!!!!!!!!!!!!!
این ماراتن هم که میگی این جا اصلا فایده و اثری نداره چون هم تعداد المپیادی های آنلاین کمه و هم بچه ها پایه نیستند.
این کار تو mathlinks فایده داره.
درسته؟
من هر چی فکر میکنم این سوال جزو هیچ کدوم از این دوتا هدف نمیتونه باشه!!!!!!!!!!!!!
این ماراتن هم که میگی این جا اصلا فایده و اثری نداره چون هم تعداد المپیادی های آنلاین کمه و هم بچه ها پایه نیستند.
این کار تو mathlinks فایده داره.
درسته؟
- ارسال ها
- 335
- لایک ها
- 8
- امتیاز
- 0
مساله ی بعدی :
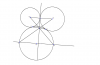
سه دایره با مرکزهای O[SUB]1[/SUB] , O[SUB]2[/SUB] , O[SUB]3[/SUB] دو به دو بر هم مماسند.محل مماس O[SUB]3[/SUB] , O[SUB]2[/SUB] را P و محل مماس O[SUB]1[/SUB] , O[SUB]3[/SUB] را Q بنامید.
BA قطری از دایره ی O[SUB]3[/SUB] میباشد که با O[SUB]1[/SUB]O[SUB]2[/SUB] موازی است.
ثابت کنید محل طلاقی O[SUB]1[/SUB]A و O[SUB]2[/SUB]B روی PQ و هم روی مماس مشترک O[SUB]1[/SUB]O[SUB]2[/SUB] قرار دارد.
سه دایره با مرکزهای O[SUB]1[/SUB] , O[SUB]2[/SUB] , O[SUB]3[/SUB] دو به دو بر هم مماسند.محل مماس O[SUB]3[/SUB] , O[SUB]2[/SUB] را P و محل مماس O[SUB]1[/SUB] , O[SUB]3[/SUB] را Q بنامید.
BA قطری از دایره ی O[SUB]3[/SUB] میباشد که با O[SUB]1[/SUB]O[SUB]2[/SUB] موازی است.
ثابت کنید محل طلاقی O[SUB]1[/SUB]A و O[SUB]2[/SUB]B روی PQ و هم روی مماس مشترک O[SUB]1[/SUB]O[SUB]2[/SUB] قرار دارد.
پیوست ها
-
24.1 کیلوبایت بازدیدها 141
seifi_seifi گفت
مساله ی بعدی :
سه دایره با مرکزهای O[SUB]1[/SUB] , O[SUB]2[/SUB] , O[SUB]3[/SUB] دو به دو بر هم مماسند.محل مماس O[SUB]3[/SUB] , O[SUB]2[/SUB] را P و محل مماس O[SUB]1[/SUB] , O[SUB]3[/SUB] را Q بنامید.
BA قطری از دایره ی O[SUB]3[/SUB] میباشد که با O[SUB]1[/SUB]O[SUB]2[/SUB] موازی است.
ثابت کنید محل طلاقی O[SUB]1[/SUB]A و O[SUB]2[/SUB]B روی PQ و هم روی مماس مشترک O[SUB]1[/SUB]O[SUB]2[/SUB] قرار دارد.
سه دایره با مرکزهای O[SUB]1[/SUB] , O[SUB]2[/SUB] , O[SUB]3[/SUB] دو به دو بر هم مماسند.محل مماس O[SUB]3[/SUB] , O[SUB]2[/SUB] را P و محل مماس O[SUB]1[/SUB] , O[SUB]3[/SUB] را Q بنامید.
BA قطری از دایره ی O[SUB]3[/SUB] میباشد که با O[SUB]1[/SUB]O[SUB]2[/SUB] موازی است.
ثابت کنید محل طلاقی O[SUB]1[/SUB]A و O[SUB]2[/SUB]B روی PQ و هم روی مماس مشترک O[SUB]1[/SUB]O[SUB]2[/SUB] قرار دارد.
- ارسال ها
- 335
- لایک ها
- 8
- امتیاز
- 0
Goharshady گفت
seifi_seifi گفت
معمولا سوال هایی رو که هر کی میزاره دو تا هدف داره : 1- خودش حل نکرده 2-یا خیلی قشنگ و جدیده که میخواد دیگران هم استفاده کنند.
من هر چی فکر میکنم این سوال جزو هیچ کدوم از این دوتا هدف نمیتونه باشه!!!!!!!!!!!!!
این ماراتن هم که میگی این جا اصلا فایده و اثری نداره چون هم تعداد المپیادی های آنلاین کمه و هم بچه ها پایه نیستند.
این کار تو mathlinks فایده داره.
درسته؟
من هر چی فکر میکنم این سوال جزو هیچ کدوم از این دوتا هدف نمیتونه باشه!!!!!!!!!!!!!
این ماراتن هم که میگی این جا اصلا فایده و اثری نداره چون هم تعداد المپیادی های آنلاین کمه و هم بچه ها پایه نیستند.
این کار تو mathlinks فایده داره.
درسته؟
ولی تعداد افراد پایه خیلی کم هستند. یکی منم یکی shoki و بعضی وقتها sabbasizadeh و بعضی وقتها هم eskandari.
dar safheye 57 az ketabe MR.Ahmadpour darim ke PA & PB az D, mahalle tamase O1 & O2 migzaran. va momas moshtarake O1 & O2 be AB amude.
DT ertefa'e ABD ast.
hamreC'e AO1 & BO2 & DT be rahaT ba Ceva sabet mishe.
X mahalle barkhorde PQ va DT ast.
Y mahalle barkhorde AO1 va DT ast.
be asani sabet mishe ke DX/XT = DY/YT. pas hokm sabet shod.
bebakhshid ke kamel naneveshtam ...l
MasAle: S mahalle barkhorde AB & DT ast. sabet konid D markaze dayereye mohaT khareG'e SPQ ast.l
DT ertefa'e ABD ast.
hamreC'e AO1 & BO2 & DT be rahaT ba Ceva sabet mishe.
X mahalle barkhorde PQ va DT ast.
Y mahalle barkhorde AO1 va DT ast.
be asani sabet mishe ke DX/XT = DY/YT. pas hokm sabet shod.
bebakhshid ke kamel naneveshtam ...l
MasAle: S mahalle barkhorde AB & DT ast. sabet konid D markaze dayereye mohaT khareG'e SPQ ast.l