ماراتن نظریه ی اعداد (سطح پیشرفته)
mousavi گفت
8
فرض کنید
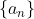یک تصاعد حسابی از اعداد طبیعی باشد.برای هر n ,
بزرگ ترین عامل اول
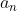میباشد.ثابت کنید دنباله
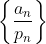غیر کراندار می باشد.
فرض کنید
بزرگ ترین عامل اول
حالا p رو یه عدد اول بگیرید که p به پیمانه a یک باشد و p از همه ی عوامل a+b بزرگتر باشه .
اعداد به شکل
پاسخ : ماراتن نظریه ی اعداد (سطح پیشرفته)
عدد اول p مخالف 2 را در نظر می گیریم
a+1 ثابت است اما n متغیر است و می تواند 3k+1 یا 3k+2 یا 3k باشد. پس تناقض حاصل نشان می دهد که اگر مکعب کامل باشد باید توانی از دو باشد.
اگر a برابر 1 نباشد a>1 پس
(1)
اگر a به شکل 4k+1 باشد آنگاه برابری 1 برقرار نیست پس a به شکل 4k+3 است که برای n های روج برابری 1 برقرار نیست پس عدد مورد نظر توانی از 2 هم نیست که بزرگتر از 8 باشد .
پس فقط a می تواند 1 باشد
عدد اول p مخالف 2 را در نظر می گیریم
a+1 ثابت است اما n متغیر است و می تواند 3k+1 یا 3k+2 یا 3k باشد. پس تناقض حاصل نشان می دهد که اگر مکعب کامل باشد باید توانی از دو باشد.
اگر a برابر 1 نباشد a>1 پس
اگر a به شکل 4k+1 باشد آنگاه برابری 1 برقرار نیست پس a به شکل 4k+3 است که برای n های روج برابری 1 برقرار نیست پس عدد مورد نظر توانی از 2 هم نیست که بزرگتر از 8 باشد .
پس فقط a می تواند 1 باشد
پاسخ : ماراتن نظریه ی اعداد (سطح پیشرفته)
بله این لم دو خط بود که جزوه ی کاملشو تو سایت بچه های 26 می تونید دانلود کنید:
المپیاد ریاضی - بچه های 26
بله این لم دو خط بود که جزوه ی کاملشو تو سایت بچه های 26 می تونید دانلود کنید:
المپیاد ریاضی - بچه های 26
- ارسال ها
- 32
- لایک ها
- 8
- امتیاز
- 0
پاسخ : ماراتن نظریه ی اعداد (سطح پیشرفته)
تمام مقادیر ممکن بزرگ مقسوم علیه 2^{2n+1}+2^1}+{n+1 و 2^{2m+1}+2^{m+1}+1 را بیابید که در آن \left (2n+1, \right 2m+1) .
ظاهرا سوال در سطح سوال 1 مرحله 2 های متوسط/سخت+ به حساب می آد. ولی من به شخصه اینو سوال 2 مناسب تر می دونم برا مقایسه ی مرحله 2 ای با این رده. دلیلی هم پیش خودم برای این حرفم دارم.
من از آقای شریفی همین جا خواهش می کنم دوباره برامون سوال بنویسن و از دوستانی که تصمیم دارند جواب سوالی را بنویسند برای استدامت بیشتر از طرف نویسندگان سوال و برای قابل استفاده بودن سوالات برای همه بی زحمت لا اقل مختصر و مفید توضیحی راجع به حل بدهند. یه موضوع دیگه اینه لازم نیست اگه حوصله ندارید سوالو حلشو بنویسید بیاید و حتما پستی مثلا با محتوی این که این سوال با 'ویتا جامپینگ' یا چیزی مث اون show off کنین. منظورم اینه که یا ننویسین با برای همه بنویسین.
مر30
تمام مقادیر ممکن بزرگ مقسوم علیه 2^{2n+1}+2^1}+{n+1 و 2^{2m+1}+2^{m+1}+1 را بیابید که در آن \left (2n+1, \right 2m+1) .
ظاهرا سوال در سطح سوال 1 مرحله 2 های متوسط/سخت+ به حساب می آد. ولی من به شخصه اینو سوال 2 مناسب تر می دونم برا مقایسه ی مرحله 2 ای با این رده. دلیلی هم پیش خودم برای این حرفم دارم.
من از آقای شریفی همین جا خواهش می کنم دوباره برامون سوال بنویسن و از دوستانی که تصمیم دارند جواب سوالی را بنویسند برای استدامت بیشتر از طرف نویسندگان سوال و برای قابل استفاده بودن سوالات برای همه بی زحمت لا اقل مختصر و مفید توضیحی راجع به حل بدهند. یه موضوع دیگه اینه لازم نیست اگه حوصله ندارید سوالو حلشو بنویسید بیاید و حتما پستی مثلا با محتوی این که این سوال با 'ویتا جامپینگ' یا چیزی مث اون show off کنین. منظورم اینه که یا ننویسین با برای همه بنویسین.
مر30
