ماراتن نظریه ی اعداد (سطح پیشرفته)
- ارسال ها
- 32
- لایک ها
- 8
- امتیاز
- 0
پاسخ : ماراتن نظریه ی اعداد (سطح پیشرفته)
واضحه دیگه بعدش نتیجه گرفته می شه که 5 ه یه خورده به معنی اون چیزی که نوشته شده فقط فکر کن من اصلا نگفتم جواب گستره ی بیشتری داره. اون راهنمایی بود نه حل! خب البته این حداقل روش حل من بود نمی دونم شاید شما منظورتون یه راه ساده تر باشه کی می دونه. سوالیم که نوشته شده بود در سطح و در زمان مرحله 2 مطرح شده بود. فک نمی کنم انتظار بره سوالی باشه موضوع پیچیده ای رو بطلبه! به هر صورت دیگه...
peace
واضحه دیگه بعدش نتیجه گرفته می شه که 5 ه یه خورده به معنی اون چیزی که نوشته شده فقط فکر کن من اصلا نگفتم جواب گستره ی بیشتری داره. اون راهنمایی بود نه حل! خب البته این حداقل روش حل من بود نمی دونم شاید شما منظورتون یه راه ساده تر باشه کی می دونه. سوالیم که نوشته شده بود در سطح و در زمان مرحله 2 مطرح شده بود. فک نمی کنم انتظار بره سوالی باشه موضوع پیچیده ای رو بطلبه! به هر صورت دیگه...
peace
پاسخ : ماراتن نظریه ی اعداد (سطح پیشرفته)
۱) ما که با هم دعوا نداریم !! peace :115::115: (نوشتت خشمگینه !)
۲) من به جای اون کار یه همنهشتی رو به توان ۴ رسوندم ، که همون چیزی که میگی رو نتیجه میده نهایتأ...
۳) شنیدم که قبول میشی مرحله ۲ ، پس بهت از الان تبریک میگم:210: ...
۴) میشه بگی منبع سوال کجا بوده ؟
واضحه دیگه بعدش نتیجه گرفته می شه که 5 ه یه خورده به معنی اون چیزی که نوشته شده فقط فکر کن من اصلا نگفتم جواب گستره ی بیشتری داره. اون راهنمایی بود نه حل! خب البته این حداقل روش حل من بود نمی دونم شاید شما منظورتون یه راه ساده تر باشه کی می دونه. سوالیم که نوشته شده بود در سطح و در زمان مرحله 2 مطرح شده بود. فک نمی کنم انتظار بره سوالی باشه موضوع پیچیده ای رو بطلبه! به هر صورت دیگه...
peace
peace
۲) من به جای اون کار یه همنهشتی رو به توان ۴ رسوندم ، که همون چیزی که میگی رو نتیجه میده نهایتأ...
۳) شنیدم که قبول میشی مرحله ۲ ، پس بهت از الان تبریک میگم:210: ...
۴) میشه بگی منبع سوال کجا بوده ؟
- ارسال ها
- 32
- لایک ها
- 8
- امتیاز
- 0
پاسخ : ماراتن نظریه ی اعداد (سطح پیشرفته)
خودمم حس کردم یه خورده تنده، peace زو نوشته بودم کمتر قیافش خمشگین باشه! حالا اگه ناراحتت کردش عذر می خوام.
من خب اونی که منم نوشتم اتحاد سوفی ژرمنه.
مر30 ولی نتایج که هنوز نیومده. به نظر من کفو نمی شه گفت برا پارسال هم چقدر همه عدد دادن آخر اون قدر کف رفت بالا. شاید من اون زمان فقط یه نفرو پیدا کردم که فک می کرد +35 می شه. خدا می دونه... باید وایسیم ببینیم. خب منم با اطلاعاتی که دارم به شما که شما قبول باید بشی. لذا منم به شما همین تبریکو می گم.
نمی دونم منبع سوالو اون زمانا که سوالو نوشتم، تو سوالای امتحان آمادگی که از بچه های انرژی اتمی تهران از بچه هاشون گرفته بودن، سوال 1 شون بود که به یک دلیلی که نمی خوام بگم فک می کنم بهتر بود اونو سوال 2 امتحان می دادن. می تونی خودت از آقای حمیدی بپرسی. اون جور که من فهمیده بودم اون بود که سوال رو داده بود!؟ در کل که به نظر منم سوال آسونی بود نمی دونم از جون منبعش چی می خوای<= این خشم نیستا حرف زدن منه:223: .
Good Luck
خودمم حس کردم یه خورده تنده، peace زو نوشته بودم کمتر قیافش خمشگین باشه! حالا اگه ناراحتت کردش عذر می خوام.
من خب اونی که منم نوشتم اتحاد سوفی ژرمنه.
مر30 ولی نتایج که هنوز نیومده. به نظر من کفو نمی شه گفت برا پارسال هم چقدر همه عدد دادن آخر اون قدر کف رفت بالا. شاید من اون زمان فقط یه نفرو پیدا کردم که فک می کرد +35 می شه. خدا می دونه... باید وایسیم ببینیم. خب منم با اطلاعاتی که دارم به شما که شما قبول باید بشی. لذا منم به شما همین تبریکو می گم.
نمی دونم منبع سوالو اون زمانا که سوالو نوشتم، تو سوالای امتحان آمادگی که از بچه های انرژی اتمی تهران از بچه هاشون گرفته بودن، سوال 1 شون بود که به یک دلیلی که نمی خوام بگم فک می کنم بهتر بود اونو سوال 2 امتحان می دادن. می تونی خودت از آقای حمیدی بپرسی. اون جور که من فهمیده بودم اون بود که سوال رو داده بود!؟ در کل که به نظر منم سوال آسونی بود نمی دونم از جون منبعش چی می خوای<= این خشم نیستا حرف زدن منه:223: .
Good Luck
پاسخ : ماراتن نظریه ی اعداد (سطح پیشرفته)
خب میدونیم که
 به پیمانه دو به توان مثلا y(ببخشید این طوری نوشتم)
به پیمانه دو به توان مثلا y(ببخشید این طوری نوشتم)
خب حالا باید اون عبارت بدون 3به توان n ها و اینا ثابت کنیم که اینم اینطوری فرض میکنیم که یه مجموعه 2n+1عضوی داریم خب میدونیم که تعداد زیر مجموعه ها فرد عضوی با تعداد زیرمجموعه های زوج عضوی(منظور از زوج عضوی اینه که تعداد اعضا زوج باشد)برابر است خب حالا داریم
 که اینم به وضوح برقراره
که اینم به وضوح برقراره
خب میدونیم که
خب حالا باید اون عبارت بدون 3به توان n ها و اینا ثابت کنیم که اینم اینطوری فرض میکنیم که یه مجموعه 2n+1عضوی داریم خب میدونیم که تعداد زیر مجموعه ها فرد عضوی با تعداد زیرمجموعه های زوج عضوی(منظور از زوج عضوی اینه که تعداد اعضا زوج باشد)برابر است خب حالا داریم
پاسخ : ماراتن نظریه ی اعداد (سطح پیشرفته)
اگر
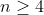 باشه
باشه
توجه کن که مرتبه 3 به پیمانه ی
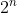 برابر
برابر
 . پس نمیتوانید به جای عدد 3 در عبارت داده شده به راحتی یک قرار بدید.
. پس نمیتوانید به جای عدد 3 در عبارت داده شده به راحتی یک قرار بدید.
خب میدونیم که
 به پیمانه دو به توان مثلا y(ببخشید این طوری نوشتم)
به پیمانه دو به توان مثلا y(ببخشید این طوری نوشتم)
خب حالا باید اون عبارت بدون 3به توان n ها و اینا ثابت کنیم که اینم اینطوری فرض میکنیم که یه مجموعه 2n+1عضوی داریم خب میدونیم که تعداد زیر مجموعه ها فرد عضوی با تعداد زیرمجموعه های زوج عضوی(منظور از زوج عضوی اینه که تعداد اعضا زوج باشد)برابر است خب حالا داریم
 که اینم به وضوح برقراره
که اینم به وضوح برقراره
خب حالا باید اون عبارت بدون 3به توان n ها و اینا ثابت کنیم که اینم اینطوری فرض میکنیم که یه مجموعه 2n+1عضوی داریم خب میدونیم که تعداد زیر مجموعه ها فرد عضوی با تعداد زیرمجموعه های زوج عضوی(منظور از زوج عضوی اینه که تعداد اعضا زوج باشد)برابر است خب حالا داریم
توجه کن که مرتبه 3 به پیمانه ی
آخرین ویرایش توسط مدیر
