ماراتن نظریه ی اعداد (سطح پیشرفته)
- ارسال ها
- 284
- لایک ها
- 272
- امتیاز
- 63
پاسخ : ماراتن نظریه ی اعداد (سطح پیشرفته)
بله خوب به همین خاطرم گذاشتمش تو پیشرفته ولی جهانیه
---- دو نوشته به هم متصل شده است ----
منتقل شد به بخش ممتاز
بله خوب به همین خاطرم گذاشتمش تو پیشرفته ولی جهانیه
---- دو نوشته به هم متصل شده است ----
اگر a,b طبیعی باشند نشان دهید اگر
 عدد
عدد
 را عاد کند آنگاه
را عاد کند آنگاه




آخرین ویرایش توسط مدیر
- ارسال ها
- 935
- لایک ها
- 1,654
- امتیاز
- 93
پاسخ : ماراتن نظریه ی اعداد (سطح پیشرفته)
حقیقتش من تصور نمی کردم بچه های تشنه فعالیت هستند در سایت !!! به خاطر همین در چند جا هم گفته بودم که دیگه قسمت ریاضی از رونق افتاده !
اما دیروز که یکی از رفقا دو تاپیک ماراتن جبر و اعداد گذاشتند خیلی خوب استقبال شد هرچند جناب math بستند و صدالبته به حق هم بستند !
اما ادامش اینجا باشه که به قوانین هم عمل بشه دیگه ! فقط اینکه سوال ها خیلی سنگین نباشه در حد مرحله دو یا یه خرده بیشتر باشه بهتره تا آمادگی مرحله دو رو ایجاد کنه در بچه ها !
شاید مثل قدیما نشه ، اما میشه به یه جایی خوبی رسوند ! اگه این عطش در درون همه باقی بمونه ! به امید خدا یاعلی استارت کار رو بزنیم !
حقیقتش من تصور نمی کردم بچه های تشنه فعالیت هستند در سایت !!! به خاطر همین در چند جا هم گفته بودم که دیگه قسمت ریاضی از رونق افتاده !
اما دیروز که یکی از رفقا دو تاپیک ماراتن جبر و اعداد گذاشتند خیلی خوب استقبال شد هرچند جناب math بستند و صدالبته به حق هم بستند !
اما ادامش اینجا باشه که به قوانین هم عمل بشه دیگه ! فقط اینکه سوال ها خیلی سنگین نباشه در حد مرحله دو یا یه خرده بیشتر باشه بهتره تا آمادگی مرحله دو رو ایجاد کنه در بچه ها !
شاید مثل قدیما نشه ، اما میشه به یه جایی خوبی رسوند ! اگه این عطش در درون همه باقی بمونه ! به امید خدا یاعلی استارت کار رو بزنیم !
- ارسال ها
- 18
- لایک ها
- 13
- امتیاز
- 3
پاسخ : ماراتن نظریه ی اعداد (سطح پیشرفته)
برای اثبات حکم کافی است نشان دهیم که معادله ی روبرو با شرط n<m جواب ندارد
 . اگر این معادله دارای جواب باشد انگاه میتوان فرض کرد که n , p نسبت به هم اولند در این صورت خواهیم داشت :
. اگر این معادله دارای جواب باشد انگاه میتوان فرض کرد که n , p نسبت به هم اولند در این صورت خواهیم داشت :
 و چون p عددی به شکل 3k+2 است و عوامل اول
و چون p عددی به شکل 3k+2 است و عوامل اول
 یا 3 و یا به شکل 3k+2 هستند پس خواهیم داشت :
یا 3 و یا به شکل 3k+2 هستند پس خواهیم داشت :
 یعنی
یعنی
 اکنون اگر در معادله اصلی به جای a عبارت بدست امده را قرار دهیم معادله به شکل زیر در می اید :
اکنون اگر در معادله اصلی به جای a عبارت بدست امده را قرار دهیم معادله به شکل زیر در می اید :
 یا به طور مرتب تر :
یا به طور مرتب تر :
 که در این صورت خواهیم داشت :
که در این صورت خواهیم داشت :
 که تناقض است و در نتیجه معادله اولیه جواب ندارد .
که تناقض است و در نتیجه معادله اولیه جواب ندارد .
برای اثبات حکم کافی است نشان دهیم که معادله ی روبرو با شرط n<m جواب ندارد
- ارسال ها
- 18
- لایک ها
- 13
- امتیاز
- 3
پاسخ : ماراتن نظریه ی اعداد (سطح پیشرفته)
اگر
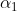 فرد باشد خواهیم داشت :
فرد باشد خواهیم داشت :
 که با توجه به زوج بودن 1+
که با توجه به زوج بودن 1+
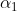 خواهیم داشت
خواهیم داشت
 که با توجه به عبارت بالا میتوان نتیجه گرفت :
که با توجه به عبارت بالا میتوان نتیجه گرفت :
 و چون
و چون
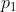 کوچکترین عامل اول n میباشد پس
کوچکترین عامل اول n میباشد پس
 و
و
 که اگر حاصل را در عبارت ابتدایی جاگزین کنیم و پس از کمی ساده کردن خواهیم داشت :
که اگر حاصل را در عبارت ابتدایی جاگزین کنیم و پس از کمی ساده کردن خواهیم داشت :
 که با مقایسه دو طرف این تساوی به سادگی نتیجه میشود که :
که با مقایسه دو طرف این تساوی به سادگی نتیجه میشود که :
 که به سادگی میتوان نتیجه گرفت که این نابرابری به طوراکید جواب ندارد و تنها حالت تساوی میتوان رخ دهد که در این حالت
که به سادگی میتوان نتیجه گرفت که این نابرابری به طوراکید جواب ندارد و تنها حالت تساوی میتوان رخ دهد که در این حالت
 و همچنین در این حالت n نمیتواند عامل اولی غیر از 2 و3 داشته باشد و به عبارتی n=6 که با n>6 در تناقض است و فرض اولیه غلط بوده و
و همچنین در این حالت n نمیتواند عامل اولی غیر از 2 و3 داشته باشد و به عبارتی n=6 که با n>6 در تناقض است و فرض اولیه غلط بوده و
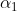 عددی زوج است .
عددی زوج است .
اگر
پاسخ : ماراتن نظریه ی اعداد (سطح پیشرفته)
میدانیم که a ,b هر دو زوج هستند. فرض کنید a=2m و b=2nدر نتیجه :
)
اما عبارت داخل قدرمطلق بزرگتر مساوی 4 هست. چون به هنگ 3 و 2 به ترتیب 1 و 0 هست.

اما به ازای هر n مقدار n^2 کوچکتر از 3 به توان n هست. در نتیجه :

پس تنها مقدار a برابر 4 است. بقیه فک کنم دیگه ساده باشه. یه سری چک کردن سادس چون n هم محدود میشه.
میدانیم که a ,b هر دو زوج هستند. فرض کنید a=2m و b=2nدر نتیجه :
اما عبارت داخل قدرمطلق بزرگتر مساوی 4 هست. چون به هنگ 3 و 2 به ترتیب 1 و 0 هست.
اما به ازای هر n مقدار n^2 کوچکتر از 3 به توان n هست. در نتیجه :
پس تنها مقدار a برابر 4 است. بقیه فک کنم دیگه ساده باشه. یه سری چک کردن سادس چون n هم محدود میشه.

