پاسخ : ماراتن نظریه ی اعداد (سطح پیشرفته)
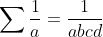
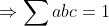

حالا چون صرفا ما میخوایم یه جواب پیدا کنیم میتونیم فرض کنیم که

نتیجه:


 حالا اگر بزاریم
حالا اگر بزاریم
 نتیجه میشه
نتیجه میشه

و یه مجموعه جواب زیر رو داریم:
 بقیش دیگه مثال زدنو ایناس که زیاد سخت نیست :4:
بقیش دیگه مثال زدنو ایناس که زیاد سخت نیست :4:
---- دو نوشته به هم متصل شده است ----
سوال بعد:
عدد طبیعی
 را شیک(!) مینامیم اگر حداقل یکی از مضاربش با
را شیک(!) مینامیم اگر حداقل یکی از مضاربش با
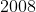 شروع شود برای مثال
شروع شود برای مثال
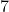 شیک است زیرا
شیک است زیرا
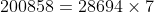
ثابت کنید تمام اعداد طبیعی شیکند.
حالا چون صرفا ما میخوایم یه جواب پیدا کنیم میتونیم فرض کنیم که
نتیجه:
و یه مجموعه جواب زیر رو داریم:
---- دو نوشته به هم متصل شده است ----
سوال بعد:
عدد طبیعی
ثابت کنید تمام اعداد طبیعی شیکند.
