با توجه به اينكه در قسمت جبر ممتاز ماراتني وجود نداره و قسمت جبر هم زياد فعال نيست با اجازه ي جناب math تصميم به ايجاد كردن اين ماراتن گرفتم. قوانين هم ايناست:
١- فقط فارسي بنويسيد.
٢- تا سوال حل نشده اي وجود داره سوال جديدي نذاريد.
٣- هر كس سوالي رو حل كرد بايد سوال بعدي رو خودش بذاره.
٤- سوالات در سطح مرحله دو و بالاتر باشه.
سوال اول رو من ميذارم و اميدوارم اين ماراتن هم رونق بگيره.
تمام توابع
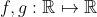 رو بيابيد به طوري كه براي هر
رو بيابيد به طوري كه براي هر
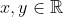 داشته باشيم:
داشته باشيم:

١- فقط فارسي بنويسيد.
٢- تا سوال حل نشده اي وجود داره سوال جديدي نذاريد.
٣- هر كس سوالي رو حل كرد بايد سوال بعدي رو خودش بذاره.
٤- سوالات در سطح مرحله دو و بالاتر باشه.
سوال اول رو من ميذارم و اميدوارم اين ماراتن هم رونق بگيره.
تمام توابع
