ماراتن جبر (سطح ممتاز)
پاسخ : ماراتن جبر (سطح ممتاز)
همون اولش كه دو تا متغيرو مساوي گذاشتين ديگه اثبات تموم بود چون از اونجا نتيجه ميشه
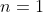 و با جايگذاري توي صورت سوال بدست مياد
و با جايگذاري توي صورت سوال بدست مياد
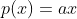 .
.
سوال بعد:
براي اعداد مثبت
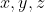 نشان دهيد
نشان دهيد

فک کنم باید اون سیگماها رو پا کنم و اون iرو به عنوان بزرگتزین توان در نظر بگیرم اونوخت درس میشه چون من اول با این روش حل کرده بودم
سوال بعد:
براي اعداد مثبت
آخرین ویرایش توسط مدیر
پاسخ : ماراتن جبر (سطح ممتاز)
سوالات بعد
1- تمام توابع از
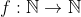 رابیابید که:
رابیابید که:

2- تمام توابع از
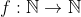 رابیابید که:
رابیابید که:

و مقدارf اعداد اول اول باشد.
3- تمام توابع یک به یک از
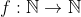 رابیابید که:
رابیابید که:

4- تمام توابع از
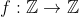 رابیابید که:
رابیابید که:

5- تمام توابع از
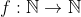 رابیابید که:
رابیابید که:

6- تمام توابع از
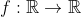 رابیابید که:
رابیابید که:

7- تمام توابع از
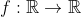 رابیابید که:
رابیابید که:

8- تمام توابع از
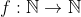 رابیابید که:
رابیابید که:

9-نامساوی زیر را اثبات کنید.
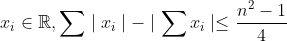
که در آن
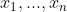 حقیقی و فاصله هر دو
حقیقی و فاصله هر دو
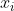 متوالی کم تر مساوی یک است
متوالی کم تر مساوی یک است
10-تمام چند جمله ای ها با ضرایب حقیقی را بیابید که

11- تمام چند جمله ای ها با ضرایب مختلط رابیابید که
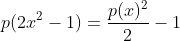
سوالات بعد
1- تمام توابع از
2- تمام توابع از
و مقدارf اعداد اول اول باشد.
3- تمام توابع یک به یک از
4- تمام توابع از
5- تمام توابع از
6- تمام توابع از
7- تمام توابع از
8- تمام توابع از
9-نامساوی زیر را اثبات کنید.
که در آن
10-تمام چند جمله ای ها با ضرایب حقیقی را بیابید که
11- تمام چند جمله ای ها با ضرایب مختلط رابیابید که
پاسخ : ماراتن جبر (سطح ممتاز)
2-
 پس
پس
 اول نيست كه تناقضه.
اول نيست كه تناقضه.
3- فرض مي كنيم وجود داشته باشه
 اي كه
اي كه
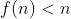 باشه. پس داريم:
باشه. پس داريم:
 به همين ترتيب براي هر
به همين ترتيب براي هر
 طبيعي داريم
طبيعي داريم
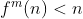 چون
چون
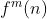 ها متناهي مقدار مي تونن بگيرن
ها متناهي مقدار مي تونن بگيرن
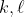 اي وجود دارند كه
اي وجود دارند كه
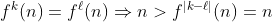 كه تناقضه پس براي هر
كه تناقضه پس براي هر
 طبيعي
طبيعي
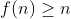 ئه. با استفاده از اين رابطه داريم:
ئه. با استفاده از اين رابطه داريم:
 4- واضحه كه
4- واضحه كه
 ثابت نيست پس داريم:
ثابت نيست پس داريم:


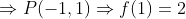
 حالا با استفاده از استقرا مي تونيم به راحتي ثابت كنيم
حالا با استفاده از استقرا مي تونيم به راحتي ثابت كنيم
 .
.
5- واضحه كه
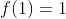 و
و
 يك به يكه. روي
يك به يكه. روي
 استقرا مي زنيم يعني فرض مي كنيم براي همه ي اعداد كوچكتر از
استقرا مي زنيم يعني فرض مي كنيم براي همه ي اعداد كوچكتر از
 تابع همانيه. اگه يكي از سه عدد سمت چپ تساوي بزرگتر از
تابع همانيه. اگه يكي از سه عدد سمت چپ تساوي بزرگتر از
 باشند وجود داره
باشند وجود داره
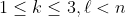 كه
كه
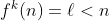 حالا بنابر فرض استقرا و يك به يكي تابع بايد داشته باشيم
حالا بنابر فرض استقرا و يك به يكي تابع بايد داشته باشيم
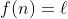 كه نتيجه ميده
كه نتيجه ميده
 و اين تناقضه پس
و اين تناقضه پس
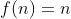 و گام استقرا ثابت ميشه.
و گام استقرا ثابت ميشه.
6- من يه سوال مشابه اين ديده بودم كه شرط اولش
 بود. شما سوالو درست نوشتين؟
بود. شما سوالو درست نوشتين؟
2-
3- فرض مي كنيم وجود داشته باشه
5- واضحه كه
6- من يه سوال مشابه اين ديده بودم كه شرط اولش
پاسخ : ماراتن جبر (سطح ممتاز)
من فكر مي كردم f همه ي اعداد اوله.
7- واضحه كه
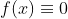 يه جوابه براي اين سوال پس فرض مي كنيم
يه جوابه براي اين سوال پس فرض مي كنيم
 اي وجود داره كه
اي وجود داره كه
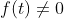 . داريم:
. داريم:



 عبارت آخر رو
عبارت آخر رو
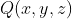 مي ناميم. داريم:
مي ناميم. داريم:
 با جايگذاري توي صورت سوال بدست مياد
با جايگذاري توي صورت سوال بدست مياد
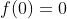 و يه جواب ديگه ي اين سوال
و يه جواب ديگه ي اين سوال
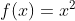 هست.
هست.
---- دو نوشته به هم متصل شده است ----
8- واضحه كه مينيمم مقدار
 براي
براي
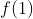 رخ ميده و
رخ ميده و
 بقيه ي اعداد از
بقيه ي اعداد از
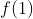 بزرگتره چون اگه مينيمم مقدار براي يه عدد ديگه مثل
بزرگتره چون اگه مينيمم مقدار براي يه عدد ديگه مثل
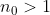 اتفاق بيافته اون وقت
اتفاق بيافته اون وقت
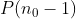 نتيجه ميده كه
نتيجه ميده كه
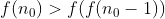 و اين تناقضه. فرض مي كنيم بعد از
و اين تناقضه. فرض مي كنيم بعد از
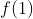 ،
،
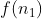 مينيمم باشه. داريم:
مينيمم باشه. داريم:
 اين هم تناقضه پس چنين تابعي وجود نداره.
اين هم تناقضه پس چنين تابعي وجود نداره.
غلط حل کردید!
الان اینکه حاصل اون تابع اول نیست تناقضی نیست نشون میده که
 اول نیست یا
اول نیست یا
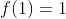 .
.
دقت کنید که گفته مقدار f اعداد اول اوله.
+ f(x)=x یه جواب بدیهی و واضح این سواله
الان اینکه حاصل اون تابع اول نیست تناقضی نیست نشون میده که
دقت کنید که گفته مقدار f اعداد اول اوله.
+ f(x)=x یه جواب بدیهی و واضح این سواله
7- واضحه كه
---- دو نوشته به هم متصل شده است ----
8- واضحه كه مينيمم مقدار
پاسخ : ماراتن جبر (سطح ممتاز)
نشان می دهیم دو تابع روبرو جواب های مساله هستند:
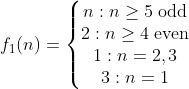
و

ابتدا توجه کنید که

حالت اول با استقرا به سادگی اثبات می شود و نکته ای ندارد. بنابراین فرض می کنیم که:
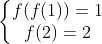
برای به دست آوردن جواب دوم نیز از استقرا استفاده می کنیم. برای این کافیست ثابت کنیم:

اینم باشه واسه بعدا.
D:
1- تمام توابع از
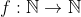 رابیابید که:
رابیابید که:

و
ابتدا توجه کنید که
حالت اول با استقرا به سادگی اثبات می شود و نکته ای ندارد. بنابراین فرض می کنیم که:
برای به دست آوردن جواب دوم نیز از استقرا استفاده می کنیم. برای این کافیست ثابت کنیم:
اینم باشه واسه بعدا.
D:
پاسخ : ماراتن جبر (سطح ممتاز)
تابع اول جواب نيست.
نشان می دهیم دو تابع روبرو جواب های مساله هستند:
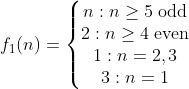
و

ابتدا توجه کنید که

حالت اول با استقرا به سادگی اثبات می شود و نکته ای ندارد. بنابراین فرض می کنیم که:
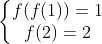
برای به دست آوردن جواب دوم نیز از استقرا استفاده می کنیم. برای این کافیست ثابت کنیم:

اینم باشه واسه بعدا.
D:
و
ابتدا توجه کنید که
حالت اول با استقرا به سادگی اثبات می شود و نکته ای ندارد. بنابراین فرض می کنیم که:
برای به دست آوردن جواب دوم نیز از استقرا استفاده می کنیم. برای این کافیست ثابت کنیم:
اینم باشه واسه بعدا.
D:
پاسخ : ماراتن جبر (سطح ممتاز)

اینم باشه واسه بعدا.
D:
editing
خب
داریم:

بنابراین:

اما از طرفی داریم:

بنابراین:

حالا باید ثابت کنیم:

که اینم معادل با اینه که:

اینم یه حالت بندی بدیهیه.
حالا کافیه ثابت کنیم:

برای اینم کافیه ثابت کنیم:

یا به طور معادل:

که این هم بدیهی است:
حالت اول:
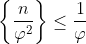 در این صورت واضحه که:
در این صورت واضحه که:
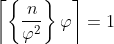 و حکم ثابت میشه.
و حکم ثابت میشه.
حالت دوم:
 .
.
پس حکم مساله ثابت شد.
---- دو نوشته به هم متصل شده است ----
اول مقادیر اولیه رو به دست میاریم:

اما:
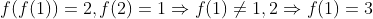
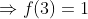
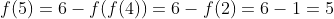
پس پایه ی استقرا جور شد.
حالا حکم استقرا:

D:
اینم باشه واسه بعدا.
D:
خب
داریم:
بنابراین:
اما از طرفی داریم:
بنابراین:
حالا باید ثابت کنیم:
که اینم معادل با اینه که:
اینم یه حالت بندی بدیهیه.
حالا کافیه ثابت کنیم:
برای اینم کافیه ثابت کنیم:
یا به طور معادل:
که این هم بدیهی است:
حالت اول:
حالت دوم:
پس حکم مساله ثابت شد.
---- دو نوشته به هم متصل شده است ----
تابع اول جواب نيست.
اما:
پس پایه ی استقرا جور شد.
حالا حکم استقرا:
D:
آخرین ویرایش توسط مدیر
