پاسخ : ماراتن نظریه اعداد (سطح مقدماتی)
فرض می کنیم دنباله ی ما به این شکل باشه:
 که
که
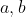 طبیعین اگه b بر هر کدوم از اعداد 2,3,5,7,11 بخشپذیر نباشه یکی از اعضای دنباله بر اون عدد بخشپذیر میشه که با اول بودن این اعداد در تناقضه. پس داریم:
طبیعین اگه b بر هر کدوم از اعداد 2,3,5,7,11 بخشپذیر نباشه یکی از اعضای دنباله بر اون عدد بخشپذیر میشه که با اول بودن این اعداد در تناقضه. پس داریم:

که تناقضه.
درسته؟
---- دو نوشته به هم متصل شده است ----
گفتم شاید استدلال قبل یکم نا مفهوم باشه اینم یه استدلال کامل تر:
مثلا یازده رو در نظر بگیرین و فرض کنید b بر 11 بخشپذیر نباشه پس برای هر دو عدد
 داریم:
داریم:

پس باقیمانده های اعداد دنباله بر 11، یازده عدد مختلفه پس حتما یکیش صفره ولی اعداد ما اولند که میشه تناقض برای بقیه هم میشه همین استدلالو به کار برد.
سوال بعد:
اگر
 عددی اول باشد ثابت کنید حداقل دو عدد اول و متمایز
عددی اول باشد ثابت کنید حداقل دو عدد اول و متمایز
 وجود دارند که برای
وجود دارند که برای
 داشته باشیم
داشته باشیم
 و
و
 .
.
ابتدا فرض کنید
 0"> .
0"> .

سپس با بررسی باقیمانده های ممکن به پیمانه 5 داریم:
 پس
پس

حال به پیمانه 6 بررسی میکنیم.

با بررسی باقیمانده های ممکن به پیمانه 7 داریم:
 و با بررسی باقیمانده های ممکن به پیمانه 13 داریم :
و با بررسی باقیمانده های ممکن به پیمانه 13 داریم :

پس
 حال اگر به پیمانه 9 بررسی کنیم
حال اگر به پیمانه 9 بررسی کنیم
 و با بررسی به پیمانه 25 داریم
و با بررسی به پیمانه 25 داریم
 پس بدیهتا
پس بدیهتا
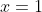 پس
پس

حال فرض کنید یکی از این اعداد 0 باشد. بدیهتا اگر
 یعنی یک جواب دیگر
یعنی یک جواب دیگر
 است. حال اگر
است. حال اگر

پس نهایتا این معادله تنها دو جواب
 و
و
 را دارد.
را دارد.
---- دو نوشته به هم متصل شده است ----
ثابت کنید دنباله ای حسابی به طول 11 از اعداد اول مثبت کوچکتر از 20000 وجود ندارد.
سپس با بررسی باقیمانده های ممکن به پیمانه 5 داریم:
حال به پیمانه 6 بررسی میکنیم.
با بررسی باقیمانده های ممکن به پیمانه 7 داریم:
پس
حال فرض کنید یکی از این اعداد 0 باشد. بدیهتا اگر
پس نهایتا این معادله تنها دو جواب
---- دو نوشته به هم متصل شده است ----
ثابت کنید دنباله ای حسابی به طول 11 از اعداد اول مثبت کوچکتر از 20000 وجود ندارد.
درسته؟
---- دو نوشته به هم متصل شده است ----
گفتم شاید استدلال قبل یکم نا مفهوم باشه اینم یه استدلال کامل تر:
مثلا یازده رو در نظر بگیرین و فرض کنید b بر 11 بخشپذیر نباشه پس برای هر دو عدد
سوال بعد:
اگر





