ماراتن نظریه اعداد (سطح مقدماتی)
- ارسال ها
- 935
- لایک ها
- 1,654
- امتیاز
- 93
پاسخ : ماراتن نظریه اعداد (سطح مقدماتی)




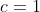
---- دو نوشته به هم متصل شده است ----
البته حالت p=2 رو باید جداگانه چک کردچون لم دو خط برای p های فرد هست و برای p=2 یه دستور دیگه داره
---- دو نوشته به هم متصل شده است ----
البته حالت p=2 رو باید جداگانه چک کردچون لم دو خط برای p های فرد هست و برای p=2 یه دستور دیگه داره
سوال بعد:
اگر p يك عدد اول باشد تمام a,b,c هاي طبيعي رابيابيد به طوريكه

اگر p يك عدد اول باشد تمام a,b,c هاي طبيعي رابيابيد به طوريكه
---- دو نوشته به هم متصل شده است ----
البته حالت p=2 رو باید جداگانه چک کردچون لم دو خط برای p های فرد هست و برای p=2 یه دستور دیگه داره
---- دو نوشته به هم متصل شده است ----
البته حالت p=2 رو باید جداگانه چک کردچون لم دو خط برای p های فرد هست و برای p=2 یه دستور دیگه داره
پاسخ : ماراتن نظریه اعداد (سطح مقدماتی)




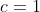
---- دو نوشته به هم متصل شده است ----
البته حالت p=2 رو باید جداگانه چک کردچون لم دو خط برای p های فرد هست و برای p=2 یه دستور دیگه داره
---- دو نوشته به هم متصل شده است ----
البته حالت p=2 رو باید جداگانه چک کردچون لم دو خط برای p های فرد هست و برای p=2 یه دستور دیگه داره
P=2 یه نزول نامتناهی شکل میده که بازم به همین جواب میرسیم یهنی(a,b,c,p)=(1,1,1,2)
---- دو نوشته به هم متصل شده است ----
البته حالت p=2 رو باید جداگانه چک کردچون لم دو خط برای p های فرد هست و برای p=2 یه دستور دیگه داره
---- دو نوشته به هم متصل شده است ----
البته حالت p=2 رو باید جداگانه چک کردچون لم دو خط برای p های فرد هست و برای p=2 یه دستور دیگه داره
پاسخ : ماراتن نظریه اعداد (سطح مقدماتی)




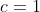
---- دو نوشته به هم متصل شده است ----
البته حالت p=2 رو باید جداگانه چک کردچون لم دو خط برای p های فرد هست و برای p=2 یه دستور دیگه داره
---- دو نوشته به هم متصل شده است ----
البته حالت p=2 رو باید جداگانه چک کردچون لم دو خط برای p های فرد هست و برای p=2 یه دستور دیگه داره
جواب شما كامل نيست چون الان a=1,b=2,c=2,p=3 هم جوابه. براي p=2 هم لم دو خط فقط براي اعداد به شكل
 تعريف شده.
تعريف شده.
---- دو نوشته به هم متصل شده است ----
نه فكر نكنم با نزول نامتناهي بشه چون ممكنه a,b فرد باشن اون وقت شما چه جوري مي خوايد نزول نامتناهي بزنين؟ براي p=2 راه هاي خيلي ساده تري هم وجود داره.
---- دو نوشته به هم متصل شده است ----
البته حالت p=2 رو باید جداگانه چک کردچون لم دو خط برای p های فرد هست و برای p=2 یه دستور دیگه داره
---- دو نوشته به هم متصل شده است ----
البته حالت p=2 رو باید جداگانه چک کردچون لم دو خط برای p های فرد هست و برای p=2 یه دستور دیگه داره
---- دو نوشته به هم متصل شده است ----
P=2 یه نزول نامتناهی شکل میده که بازم به همین جواب میرسیم یهنی(a,b,c,p)=(1,1,1,2)
- ارسال ها
- 935
- لایک ها
- 1,654
- امتیاز
- 93
پاسخ : ماراتن نظریه اعداد (سطح مقدماتی)
آخ آخ من تو تجزیه یه اشتباهی کردم !!!

با شرط a>b

پس b=1


اگه a یک نباشه پس

پس p=3 رو میده که باید چک کنیم

که باید a=2 باشه .
حالت p=2 رو هم باید چک کرد
---- دو نوشته به هم متصل شده است ----
سوال بعد :
تمام توابع f از اعداد طبیعی به خودش را بیابید که

که k یه عدد طبیعی است
آخ آخ من تو تجزیه یه اشتباهی کردم !!!
با شرط a>b
پس b=1
اگه a یک نباشه پس
پس p=3 رو میده که باید چک کنیم
که باید a=2 باشه .
حالت p=2 رو هم باید چک کرد
---- دو نوشته به هم متصل شده است ----
سوال بعد :
تمام توابع f از اعداد طبیعی به خودش را بیابید که
که k یه عدد طبیعی است
پاسخ : ماراتن نظریه اعداد (سطح مقدماتی)
نه خب دیگه فرض میکنیم c>1 و معادله رو به پیمانه 4 بررسی میکنیم اون وقت بدیهیه که هر دو باید زوج باشن!!!
جواب شما كامل نيست چون الان a=1,b=2,c=2,p=3 هم جوابه. براي p=2 هم لم دو خط فقط براي اعداد به شكل
 تعريف شده.
تعريف شده.
---- دو نوشته به هم متصل شده است ----
نه فكر نكنم با نزول نامتناهي بشه چون ممكنه a,b فرد باشن اون وقت شما چه جوري مي خوايد نزول نامتناهي بزنين؟ براي p=2 راه هاي خيلي ساده تري هم وجود داره.
---- دو نوشته به هم متصل شده است ----
نه فكر نكنم با نزول نامتناهي بشه چون ممكنه a,b فرد باشن اون وقت شما چه جوري مي خوايد نزول نامتناهي بزنين؟ براي p=2 راه هاي خيلي ساده تري هم وجود داره.
پاسخ : ماراتن نظریه اعداد (سطح مقدماتی)


آخ آخ من تو تجزیه یه اشتباهی کردم !!!

با شرط a>b

پس b=1


اگه a یک نباشه پس

پس p=3 رو میده که باید چک کنیم

که باید a=2 باشه .
حالت p=2 رو هم باید چک کرد
---- دو نوشته به هم متصل شده است ----
سوال بعد :
تمام توابع f از اعداد طبیعی به خودش را بیابید که

که k یه عدد طبیعی است
با شرط a>b
پس b=1
اگه a یک نباشه پس
پس p=3 رو میده که باید چک کنیم
که باید a=2 باشه .
حالت p=2 رو هم باید چک کرد
---- دو نوشته به هم متصل شده است ----
سوال بعد :
تمام توابع f از اعداد طبیعی به خودش را بیابید که
که k یه عدد طبیعی است
حالا میایم یه کار خوب میکنیم فرض کنیم
 ثابته و
ثابته و
 متغیر پس میتونیم
متغیر پس میتونیم
 رو طوری انتخاب کنیم که
رو طوری انتخاب کنیم که

اما طبق رابطه اولیه داریم که با توجه به اینکه
اگه حداقل دوتا از اعداد برد مثل
 زوج باشن پس یعنی داریم که توانای 2 شون برابره پس میتونیم نتیجه بگیریم
زوج باشن پس یعنی داریم که توانای 2 شون برابره پس میتونیم نتیجه بگیریم

حالا اگه
 یه عدد ثابت باشه و حداقل 2 تا از
یه عدد ثابت باشه و حداقل 2 تا از
 وجود داشته باشن که
وجود داشته باشن که

که تناقضه پس اعدادی وجود دارن که تابعشون تو برد نیست دو حالت دیگه میمونه که یکیشون سادت و رد میشه و جواب اون یکی هم تابع همانی میشه اگه خواستید بنویسم!!!
حالت دوم اینه که
 که خیلی راحت میشه فهمید همانیه و
که خیلی راحت میشه فهمید همانیه و
 حالت سوم هم اینه که یکی زوج و بقیه فرد باشن که اینم مثل حالت اول رد میشه!!!
حالت سوم هم اینه که یکی زوج و بقیه فرد باشن که اینم مثل حالت اول رد میشه!!!
اگه حداقل دوتا از اعداد برد مثل
حالا اگه
که تناقضه پس اعدادی وجود دارن که تابعشون تو برد نیست دو حالت دیگه میمونه که یکیشون سادت و رد میشه و جواب اون یکی هم تابع همانی میشه اگه خواستید بنویسم!!!
حالت دوم اینه که
آخرین ویرایش توسط مدیر
پاسخ : ماراتن نظریه اعداد (سطح مقدماتی)
يه راه ديگه:
به راحتي داريم
 با توجه به اين رابطه داريم (p يه عدد اوله):
با توجه به اين رابطه داريم (p يه عدد اوله):
 حالا اگه به جاي p دو قرار بديم بدست مياد
حالا اگه به جاي p دو قرار بديم بدست مياد
 حالا به همين ترتيب داريم:
حالا به همين ترتيب داريم:


با توجه به اين روابط مي تونيم
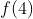 رو به دو طريق بدست بياريم كه بدست مياد:
رو به دو طريق بدست بياريم كه بدست مياد:
 حالا اگه دو طرف رو به پيمانه ي ٣ در نظر بگيريم داريم
حالا اگه دو طرف رو به پيمانه ي ٣ در نظر بگيريم داريم
 . حالا با توجه به لم دو خط داريم:
. حالا با توجه به لم دو خط داريم:
 اگه k صفر نباشه داريم
اگه k صفر نباشه داريم
 كه تناقضه. پس m=0 كه نتيجه ميده:
كه تناقضه. پس m=0 كه نتيجه ميده:
 حالا با استقرا ثابت مي كنيم
حالا با استقرا ثابت مي كنيم
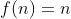 فرض مي كنيم
فرض مي كنيم

و اين رابطه براي هر k از دو تا k صحيح باشه. اول ثابت مي كنيم
 فرض مي كنيم p عددي اول بين k,2k باشه. پس حتما يكي از اعداد
فرض مي كنيم p عددي اول بين k,2k باشه. پس حتما يكي از اعداد
 برابر با k هست. حالا براي اثبات گام استقرا كافيه ثابت كنيم
برابر با k هست. حالا براي اثبات گام استقرا كافيه ثابت كنيم
 داريم:
داريم:
 حالا اگه p يك عدد اول بين k,2k باشه بدست مياد n=1 و گام استقرا ثابت ميشه. پس براي هر n طبيعي
حالا اگه p يك عدد اول بين k,2k باشه بدست مياد n=1 و گام استقرا ثابت ميشه. پس براي هر n طبيعي
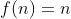 است.
است.
---- دو نوشته به هم متصل شده است ----
سوال بعد:
همه ي اعداد طبيعي x,y را بيابيد كه
 عددي طبيعي باشد.
عددي طبيعي باشد.
سوال بعد :
تمام توابع f از اعداد طبیعی به خودش را بیابید که

که k یه عدد طبیعی است
تمام توابع f از اعداد طبیعی به خودش را بیابید که
که k یه عدد طبیعی است
به راحتي داريم
و اين رابطه براي هر k از دو تا k صحيح باشه. اول ثابت مي كنيم
---- دو نوشته به هم متصل شده است ----
سوال بعد:
همه ي اعداد طبيعي x,y را بيابيد كه
پاسخ : ماراتن نظریه اعداد (سطح مقدماتی)
اگه اشتباه نکنم این سوال تکراریه فقط اونموقع 7 بجا 11 بود!!!
يه راه ديگه:
به راحتي داريم
 با توجه به اين رابطه داريم (p يه عدد اوله):
با توجه به اين رابطه داريم (p يه عدد اوله):
 حالا اگه به جاي p دو قرار بديم بدست مياد
حالا اگه به جاي p دو قرار بديم بدست مياد
 حالا به همين ترتيب داريم:
حالا به همين ترتيب داريم:


با توجه به اين روابط مي تونيم
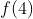 رو به دو طريق بدست بياريم كه بدست مياد:
رو به دو طريق بدست بياريم كه بدست مياد:
 حالا اگه دو طرف رو به پيمانه ي ٣ در نظر بگيريم داريم
حالا اگه دو طرف رو به پيمانه ي ٣ در نظر بگيريم داريم
 . حالا با توجه به لم دو خط داريم:
. حالا با توجه به لم دو خط داريم:
 اگه k صفر نباشه داريم
اگه k صفر نباشه داريم
 كه تناقضه. پس m=0 كه نتيجه ميده:
كه تناقضه. پس m=0 كه نتيجه ميده:
 حالا با استقرا ثابت مي كنيم
حالا با استقرا ثابت مي كنيم
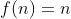 فرض مي كنيم
فرض مي كنيم

و اين رابطه براي هر k از دو تا k صحيح باشه. اول ثابت مي كنيم
 فرض مي كنيم p عددي اول بين k,2k باشه. پس حتما يكي از اعداد
فرض مي كنيم p عددي اول بين k,2k باشه. پس حتما يكي از اعداد
 برابر با k هست. حالا براي اثبات گام استقرا كافيه ثابت كنيم
برابر با k هست. حالا براي اثبات گام استقرا كافيه ثابت كنيم
 داريم:
داريم:
 حالا اگه p يك عدد اول بين k,2k باشه بدست مياد n=1 و گام استقرا ثابت ميشه. پس براي هر n طبيعي
حالا اگه p يك عدد اول بين k,2k باشه بدست مياد n=1 و گام استقرا ثابت ميشه. پس براي هر n طبيعي
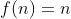 است.
است.
---- دو نوشته به هم متصل شده است ----
سوال بعد:
همه ي اعداد طبيعي x,y را بيابيد كه
 عددي طبيعي باشد.
عددي طبيعي باشد.
به راحتي داريم
و اين رابطه براي هر k از دو تا k صحيح باشه. اول ثابت مي كنيم
---- دو نوشته به هم متصل شده است ----
سوال بعد:
همه ي اعداد طبيعي x,y را بيابيد كه
- ارسال ها
- 159
- لایک ها
- 282
- امتیاز
- 0
پاسخ : ماراتن نظریه اعداد (سطح مقدماتی)
k راطوري ارائه ميدهيم كه براي هر t ، عبارت مساله مركب باشد. پس جواب نه است.
فرض كنيد k-1 بر سه -كوچكترين عدد اول فرما- بخش پذير باشد. پس اگر عبارت اول باشد واضح است كه t زوج است.
همچنين اگر k-1 بر ٥- دومين عدد فرما- بخش پذير باشد چون t زوج است بر ٤ بخش پذير است.
اگر اين عمليات را براي ١٧،٢٥٧،٦٥٥٣٧ كه اعداد اول بعدي فرما هستند پياده كنيم نتيجه ميشود t بر ٣٢ بخش پذير است.
حال k را طوري ارائه ميدهيم كه علاوه بر داشتن شروط بالا، همزمانt بر ٦٤ بخش پذير باشد و نباشد كه با وجود t كه به ازاي آن عبارت اول شود تناقض دارد.
دقت كنيد كه عدد پنجم فرما اول نيست و بر دو عدد ٦٤١ و كوفت بخش پذير است. حال k را طوري بگيريد كه به پيمانه ٦٤١ برابر ١ و به پيمانه كوفت برابر منفي يك باشد. طبق باقيمانده چيني حتما k وجود دارد كه در همه شرايط صدق كند . بديهتا چون k به پيمانه ٦٤١ برابر ١ است و عدد ٥ ام فرما بر ٦٤١ بخش پذير است t بر ٦٤ بخش پذير است. اما بديهتا اگر t بر ٦٤ بخش پذير باشد عبارت مساله بر كوفت بخش پذير ميشود، كه اگر كوفت به اندازه كافي بزرگ باشد با اول بودن عبارت متناقض است. اما باقيمانده چيني جواب هاي به اندازه كافي بزرگي ميدهد. پس حكم اثبات شد.
k راطوري ارائه ميدهيم كه براي هر t ، عبارت مساله مركب باشد. پس جواب نه است.
فرض كنيد k-1 بر سه -كوچكترين عدد اول فرما- بخش پذير باشد. پس اگر عبارت اول باشد واضح است كه t زوج است.
همچنين اگر k-1 بر ٥- دومين عدد فرما- بخش پذير باشد چون t زوج است بر ٤ بخش پذير است.
اگر اين عمليات را براي ١٧،٢٥٧،٦٥٥٣٧ كه اعداد اول بعدي فرما هستند پياده كنيم نتيجه ميشود t بر ٣٢ بخش پذير است.
حال k را طوري ارائه ميدهيم كه علاوه بر داشتن شروط بالا، همزمانt بر ٦٤ بخش پذير باشد و نباشد كه با وجود t كه به ازاي آن عبارت اول شود تناقض دارد.
دقت كنيد كه عدد پنجم فرما اول نيست و بر دو عدد ٦٤١ و كوفت بخش پذير است. حال k را طوري بگيريد كه به پيمانه ٦٤١ برابر ١ و به پيمانه كوفت برابر منفي يك باشد. طبق باقيمانده چيني حتما k وجود دارد كه در همه شرايط صدق كند . بديهتا چون k به پيمانه ٦٤١ برابر ١ است و عدد ٥ ام فرما بر ٦٤١ بخش پذير است t بر ٦٤ بخش پذير است. اما بديهتا اگر t بر ٦٤ بخش پذير باشد عبارت مساله بر كوفت بخش پذير ميشود، كه اگر كوفت به اندازه كافي بزرگ باشد با اول بودن عبارت متناقض است. اما باقيمانده چيني جواب هاي به اندازه كافي بزرگي ميدهد. پس حكم اثبات شد.
- ارسال ها
- 935
- لایک ها
- 1,654
- امتیاز
- 93
پاسخ : ماراتن نظریه اعداد (سطح مقدماتی)
اول 2 به توان a رو میبریم اونطرف.بعد mod 17 میگیریم نتیجه میشه چون طرف راست به 17 بخشپذیره طرف چپ هم بخشپذیره.پس p=17
حالا داریم 17 به توان b مساویه با 19 به توان a منهای 2 به توان a .بعدش میایم 17 رو به صورت 2-19 مینویسیم و بسط میدیم.اگه مقایسه کنیم دوتا جمله رو میبینیم که a=b .حالا داریم 17 به توان a مساویه با 19 به توان a منهای 2 به توان a.که به سادگی نتیجه میشه a=1 پس تنها جواب اینه: (p,a,b)=(17,1,1)
سوال بعد:
همه ی اعداد طبیعی
 و عدد اول
و عدد اول
 را بیابید به طوریکه
را بیابید به طوریکه
 باشد.
باشد.
همه ی اعداد طبیعی
حالا داریم 17 به توان b مساویه با 19 به توان a منهای 2 به توان a .بعدش میایم 17 رو به صورت 2-19 مینویسیم و بسط میدیم.اگه مقایسه کنیم دوتا جمله رو میبینیم که a=b .حالا داریم 17 به توان a مساویه با 19 به توان a منهای 2 به توان a.که به سادگی نتیجه میشه a=1 پس تنها جواب اینه: (p,a,b)=(17,1,1)
